|
Édition du: 03/03/2025 |
|
INDEX |
Forme retournées |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Retournés(n) = kn ± h
Le nombre est
son retourné sont liés par une relation linéaire. Ces deux nombres
sont les seuls en: R(n) = n ∙ k ± 1 avec k > 2. |
||
|
|
Sommaire de cette page >>> Relation à un près >>> Relation avec écart de 2 et plus >>> Relation et retourné par 2 >>> Relation et retourné par 3 |
Débutants Glossaire |
|
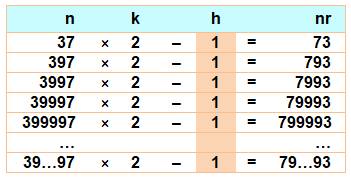
Double Le double du nombre 37 moins un est égal à son
retourné 73. Avec cette relation (2n – 1), le nombre 37 est à l'origine d'une famille
sans fin en intercalant un 9 entre deux autres 9. |
|
|
|
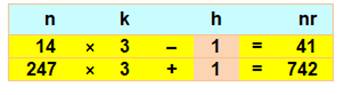
Triple Les nombres 14 et 247 sont les seuls tels que le
triple plus ou moins 1 soient leurs retournés. |
|
|
|
Quadruple et plus Aucun nombre n'est le retourné du quadruple d'un
nombre plus ou moins 1. |
/ |
|
Voir Nombre
14 / Nombre 37 / Nombre 247/ Brève 61/1216
|
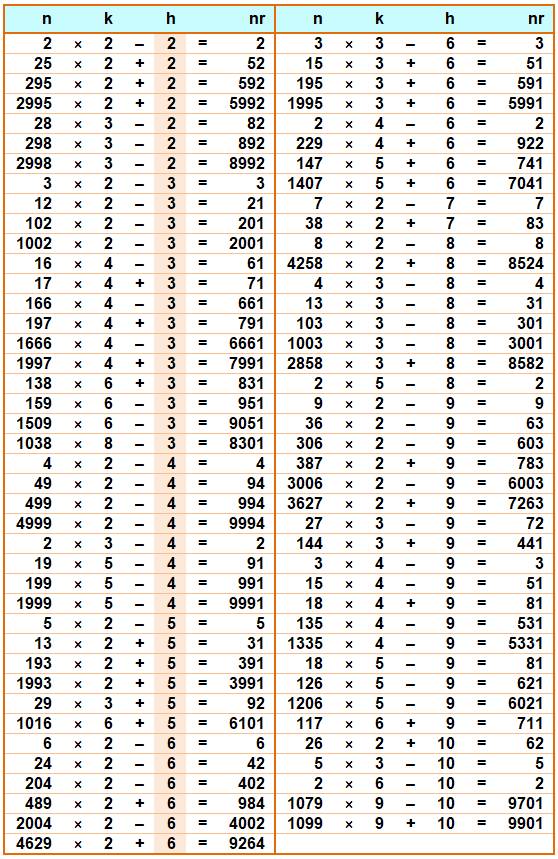
Tableau Le tableau dresse la liste des nombres jusqu'à 10000, avec un coefficient k de 2 à 10 et une constante h de 2 à 10. D'après cette liste, on imagine très bien les amorces de familles. Le nombre intercalaire est le plus souvent 9 ou 0 ou 3. Exemple avec: 135 × 4 – 9 = 531 on a: 1335 × 4 – 9 = 5331 13335 × 4 – 9 = 53331 … |
|
|
|
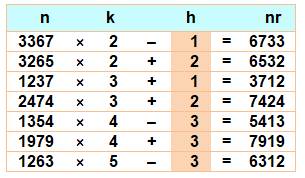
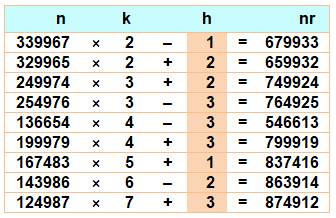
Un retourné par 2 inverse les blocs de deux
chiffres. Le tableau montre les nombres et leur retourné par 2 en relation linéaire. Entre le tableau à quatre chiffres et celui à six
chiffres, on imagine la création de familles, comme 3367 et 339967. Exemples 67 33 = 33 67 × 2 – 1 874912 = 124987 × 7 + 3 |
|
|
Voir Nombre
1237 / Nombre 1263 / Nombre 3265 / Nombre 6532
|
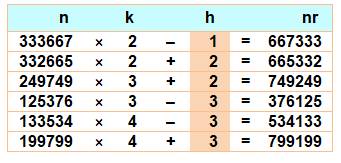
Un retourné par 3 inverse les blocs de trois
chiffres. Le tableau montre les nombres et leur retourné par 3 en relation linéaire. Entre Exemples 667 333 = 333 667 × 2 – 1 |
|
|
Voir Nombre
667333
Haut de page (ou
double-clic)
![]()
|
Voir |
|
|
Cette page |