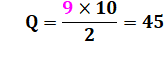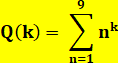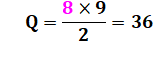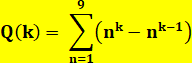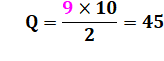Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 20/06/2023 M'écrire Brèves de Maths

INDEX Types de nombres Nombres à motifs Chiffres et opérations Nombres en chiffres	En Motifs
	Uniformes	Ondulants	Répétitions	Formes diverses
	Ascendants	Ondulants d'Euler	Zigzag (Euler)	Croissants
	Orphelins	Dominant	Zébrés	Multiples

Faites un double-clic pour un retour en haut de page

NOMBRES à chiffre dominant Dominant à gauche: le chiffre de gauche (poids fort) est plus grand que tous ceux qui suivent. Dominant à droite: le chiffre de droit (poids faible) est plus grand que tous ceux qui précédent. Combien sont-ils ?
	Sommaire de cette page >>> De 10 à 99 – Dominant à gauche >>> De 100 à 999 >>> De 1000 à 9999 >>> Dominant à gauche – Formule et liste >>> Dominant à droite – Formule et liste >>> Dominant à droite par la somme >>> Programmation Maple	Débutants Nombres Glossaire Nombres

Anglais: A digit-dominant number is a number such that

the first digit (left-dominant) or the last digit (right-dominant) is greater than any other digits

De 10 à 99 – Dominant à gauche		haut
De 1 à 9, la notion est sans objet. De 10 à 99, ils sont 45. La liste ci-contre montre qu'il s'agit de la somme des nombres de 1 à 9 qui se calcule de la façon suivante:	10, 20, 21, 30, 31, 32, (seuls 0, 1 et 2 sont inférieurs à 3) 40, 41, 42, 43, 50, 51, 52, 53, 54, 60, 61, 62, 63, 64, 65, 70, 71, 72, 73, 74, 75, 76, 80, 81, 82, 83, 84, 85, 86, 87, 90, 91, 92, 93, 94, 95, 96, 97, 98.

Voir Brève 51-1005

De 100 à 999 – Dominant à gauche

haut

Ils sont 285

Chaque centaine compte une quantité de nombres égale au carré du chiffre de la centaine.

100,	1 = 1²
200, 201, 210, 211,	4 = 2²
300, 301, 302, 310, 311, 312, 320, 321, 322, Notez qu'il y a 3 × 3 = 3^2 possibilités, et cette logique se répète pour toutes les centaines.	9 = 3²
400, 401, 402, 403, 410, 411, 412, 413, 420, 421, 422, 423, 430, 431, 432, 433,	16 = 4²
500, 501, 502, 503, 504, 510, 511, 512, 513, 514, 520, 521, 522, 523, 524, 530, 531, 532, 533, 534, 540, 541, 542, 543, 544,	25 = 5²
600, 601, 602, 603, 604, 605, 610, 611, 612, 613, 614, 615, 620, 621, 622, 623, 624, 625, 630, 631, 632, 633, 634, 635, 640, 641, 642, 643, 644, 645, 650, 651, 652, 653, 654, 655,	36 = 6²
700, 701, 702, 703, 704, 705, 706, 710, 711, 712, 713, 714, 715, 716, 720, 721, 722, 723, 724, 725, 726, 730, 731, 732, 733, 734, 735, 736, 740, 741, 742, 743, 744, 745, 746, 750, 751, 752, 753, 754, 755, 756, 760, 761, 762, 763, 764, 765, 766,	47 = 7²
800, 801, 802, 803, 804, 805, 806, 807, 810, 811, 812, 813, 814, 815, 816, 817, 820, 821, 822, 823, 824, 825, 826, 827, 830, 831, 832, 833, 834, 835, 836, 837, 840, 841, 842, 843, 844, 845, 846, 847, 850, 851, 852, 853, 854, 855, 856, 857, 860, 861, 862, 863, 864, 865, 866, 867, 870, 871, 872, 873, 874, 875, 876, 877,	64 = 8²
900, 901, 902, 903, 904, 905, 906, 907, 908, 910, 911, 912, 913, 914, 915, 916, 917, 918, 920, 921, 922, 923, 924, 925, 926, 927, 928, 930, 931, 932, 933, 934, 935, 936, 937, 938, 940, 941, 942, 943, 944, 945, 946, 947, 948, 950, 951, 952, 953, 954, 955, 956, 957, 958, 960, 961, 962, 963, 964, 965, 966, 967, 968, 970, 971, 972, 973, 974, 975, 976, 977, 978, 980, 981, 982, 983, 984, 985, 986, 987, 988.	81 =9²
1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2 + 7^2 + 8^2+ 9^2	= 285

De 1000 à 9999 – Dominant à gauche

haut

Ils sont 2025

Chaque millier compte une quantité de nombre égal au cube du chiffre de la centaine.

1000,	1 = 1^3
2000, 2001, 2010, 2011, 2100, 2101, 2110, 2111,	8 = 2^3
3000, 3001, 3002, 3010, 3011, 3012, 3020, 3021, 3022, 3100, 3101, 3102, 3110, 3111, 3112, 3120, 3121, 3122, 3200, 3201, 3202, 3210, 3211, 3212, 3220, 3221, 3222, Notez qu'il y a (3 × 3) × 3 = 3^3 possibilités, et cette logique se répète pour tous les milliers.	27 = 3^3
4000, 4001, 4002, 4003, 4010, 4011, 4012, 4013, 4020, 4021, 4022, 4023, 4030, 4031, 4032, 4033, 4100, 4101, 4102, 4103, 4110, 4111, 4112, 4113, 4120, 4121, 4122, 4123, 4130, 4131, 4132, 4133, 4200, 4201, 4202, 4203, 4210, 4211, 4212, 4213, 4220, 4221, 4222, 4223, 4230, 4231, 4232, 4233, 4300, 4301, 4302, 4303, 4310, 4311, 4312, 4313, 4320, 4321, 4322, 4323, 4330, 4331, 4332, 4333,	64 = 4^3
5000, 5001, 5002, 5003, 5004, 5010, 5011, 5012, 5013, 5014, 5020, 5021, 5022, 5023, 5024, 5030, 5031, 5032, 5033, 5034, 5040, 5041, 5042, 5043, 5044, 5100, 5101, 5102, 5103, 5104, 5110, 5111, 5112, 5113, 5114, 5120, 5121, 5122, 5123, 5124, 5130, 5131, 5132, 5133, 5134, 5140, 5141, 5142, 5143, 5144, 5200, 5201, 5202, 5203, 5204, 5210, 5211, 5212, 5213, 5214, 5220, 5221, 5222, 5223, 5224, 5230, 5231, 5232, 5233, 5234, 5240, 5241, 5242, 5243, 5244, 5300, 5301, 5302, 5303, 5304, 5310, 5311, 5312, 5313, 5314, 5320, 5321, 5322, 5323, 5324, 5330, 5331, 5332, 5333, 5334, 5340, 5341, 5342, 5343, 5344, 5400, 5401, 5402, 5403, 5404, 5410, 5411, 5412, 5413, 5414, 5420, 5421, 5422, 5423, 5424, 5430, 5431, 5432, 5433, 5434, 5440, 5441, 5442, 5443, 5444,	125 = 5^3
6000, …	16 = 6^3
	343 = 7^3
	512 = 8^3
	729 =9^3
1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3+ 9^3	= 2 025

En général – Dominant à gauche		haut
Formule Somme des puissances k des nombres de 1 à 9:	Liste pour k de 1 à 20 9, 45, 285, 2025, 15333, 120825, 978405, 8080425, 67731333, 574304985, 4914341925, 42364319625, 367428536133, 3202860761145, 28037802953445, 246324856379625, 2170706132009733, 19179318935377305, 169842891165484965, 1506994510201252425, … OEIS A001556

Dominant à droite

haut

De 10 à 99, les nombres dominants à droite sont 36.

La liste ci-contre montre qu'il s'agit de la somme des nombres de 1 à 8 qui se calcule de la façon suivante:

Notez que le triangle des possibilités est compris dans une grille 8 × 8 et non 9 × 9 comme pour les nombres dominants à gauche. Ce rang en moins se reflétera dans la formule de calcul.

De 10 à 99

12, 13, 14, 15, 16, 17, 18, 19,

23, 24, 25, 26, 27, 28, 29,

34, 35, 36, 37, 38, 39,

45, 46, 47, 48, 49,

56, 57, 58, 59,

67, 68, 69,

78, 79,

89

De 100 à 999

102, 103, 104, 105, 106, 107, 108, 109, 112, 113, 114, 115, 116, 117, 118, 119, 123, 124, 125, 126, 127, 128, 129, 134, 135, 136, 137, 138, 139, 145, 146, 147, 148, 149, 156, 157, 158, 159, 167, 168, 169, 178, 179, 189,	2×8+7+6+5+4+3+2+1 = 44
203, 204, 205, 206, 207, 208, 209, 213, 214, 215, 216, 217, 218, 219, 223, 224, 225, 226, 227, 228, 229, 234, 235, 236, 237, 238, 239, 245, 246, 247, 248, 249, 256, 257, 258, 259, 267, 268, 269, 278, 279, 289,	3×7+6+5+4+3+2+1 = 42
304, 305, 306, 307, 308, 309, 314, 315, 316, 317, 318, 319, 324, 325, 326, 327, 328, 329, 334, 335, 336, 337, 338, 339, 345, 346, 347, 348, 349, 356, 357, 358, 359, 367, 368, 369, 378, 379, 389,	4×6+5+4+3+2+1 = 39
405, 406, 407, 408, 409, 415, 416, 417, 418, 419, 425, 426, 427, 428, 429, 435, 436, 437, 438, 439, 445, 446, 447, 448, 449, 456, 457, 458, 459, 467, 468, 469, 478, 479, 489,	5×5+4+3+2+1 = 35
506, 507, 508, 509, 516, 517, 518, 519, 526, 527, 528, 529, 536, 537, 538, 539, 546, 547, 548, 549, 556, 557, 558, 559, 567, 568, 569, 578, 579, 589,	6×4+3+2+1 = 30
607, 608, 609, 617, 618, 619, 627, 628, 629, 637, 638, 639, 647, 648, 649, 657, 658, 659, 667, 668, 669, 678, 679, 689,	7×3+2+1 = 24
708, 709, 718, 719, 728, 729, 738, 739, 748, 749, 758, 759, 768, 769, 778, 779, 789,	8×2+1 = 17
809, 819, 829, 839, 849, 859, 869, 879, 889.	9×1+ 0 = 9
1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2 + 7^2 + 8^2+ 9^2 – (1+2+3+4+5+6+7+8+9)	= 285 – 45 = 240

Formule

Somme des puissances k des nombres de 1 à 9 moins la somme précédente:

Liste pour k de 1 à 20

36, 240, 1740, 13308, 105492, 857580, 7102020, 59650908, 506573652, 4340036940, 37449977700, 325064216508, 2835432225012, 24834942192300, 218287053426180, 1924381275630108, 17008612803367572, 150663572230107660, 1337151619035767460, 11887137348631299708, …

Dominant à droite par la somme

haut

Nombre tel que son chiffre de gauche est plus grand que la somme de tous les autres.

De 10 à 99, il n'y a pas de somme.

De 10 à 999 , ils sont 165

De 10 à 99

10,

20, 21,

30, 31, 32, …

Idem que dominant par la gauche

De 100 à 999

100,	1
200, 201, 210,	2+1 = 3
300, 301, 302, 310, 311, 320,	3+2+1 = 6
400, 401, 402, 403, 410, 411, 412, 420, 421, 430,	4+3+2+1 = 10
500, 501, 502, 503, 504, 510, 511, 512, 513, 520, 521, 522, 530, 531, 540,	5+4+3+2+1 = 15
600, 601, 602, 603, 604, 605, 610, 611, 612, 613, 614, 620, 621, 622, 623, 630, 631, 632, 640, 641, 650,	6+5+4+3+2+1 = 21
700, 701, 702, 703, 704, 705, 706, 710, 711, 712, 713, 714, 715, 720, 721, 722, 723, 724, 730, 731, 732, 733, 740, 741, 742, 750, 751, 760,	7+ 6+5+…+2+1 = 28
800, 801, 802, 803, 804, 805, 806, 807, 810, 811, 812, 813, 814, 815, 816, 820, 821, 822, 823, 824, 825, 830, 831, 832, 833, 834, 840, 841, 842, 843, 850, 851, 852, 860, 861, 870,	8+7+ 6+…+2+1 = 36
900, 901, 902, 903, 904, 905, 906, 907, 908, 910, 911, 912, 913, 914, 915, 916, 917, 920, 921, 922, 923, 924, 925, 926, 930, 931, 932, 933, 934, 935, 940, 941, 942, 943, 944, 950, 951, 952, 953, 960, 961, 962, 970, 971, 980	9+8+7+ …+2+1 = 45
9×1 + 8×2 + 7×3 + 6×4 + 5×5 + 4×6 + 3×7 + 2×8 + 1×9	= 165

Formule

Somme des puissances k des nombres de 1 à 9 moins la somme précédente:

Une oblique du triangle de Pascal.

Liste pour k de 1 à 31
(en bleu: confirmés par calcul)

45, 165, 495, 1287, 3003, 6435, 12870, 24310, 43758, 75582, 125970, 203490, 319770, 490314, 735471, 1081575, 1562275, 2220075, 3108105, 4292145, 5852925, 7888725, 10518300, 13884156, 18156204, 23535820, 30260340, 38608020, 48903492, 61523748, 76904685, …

OEIS A000581

Programmation Maple		haut
	But Lister tout les nombres dominants à gauche entre m et mm. Commentaires Pour chaque nombre n, décomposition en chiffres (convert). Attention, les chiffres sont listés de droite à gauche (à l'envers). Extraction du dernier chiffre (-1) qui est en fait le premier. Constitution de la liste des chiffres sans ce dominant (subsop) puis élimination des chiffres en double en formant l'ensemble S des chiffres autres que le dominant. Si un chiffre dans S est plus grand que le dominant, le témoin T est mis à 0. En fin d'analyse, si le témoin est toujours à 1, le nombre est dominant et il est enregistré dans la liste L.

Voir Programmation – Index

Haut de page (ou double-clic)

Suite	Voir Haut de page Nombres croissants et décroissants – TABLES Nombres consécutifs – Index Nombres uniformes ou repdigits Nombres repunits
Voir	Type de nombres – Index Multiplications pyramidales Nombres méandriques Nombres retournés Nombres retournés avec soustraction de 99 Nombres palindromes
Sites	OEIS A001556 – a(n) = 1^n + 2^n + ... + 9^n. Star problems – Mathschallenge.net – 2002 - Page 15: Bigger Digit
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/ChPrepon.htm