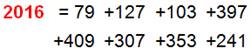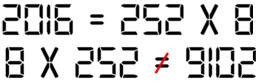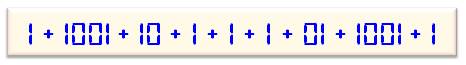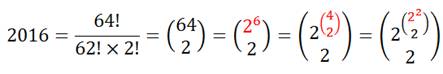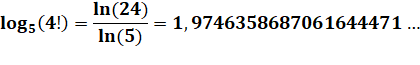|
||||||||||||||||||||||||||||||||||
Sans "s" à mille en français comme en
anglais
![]()
|
DicoNombre: NOMBRE 2016 |

Voir Défi de
la somme minimale
Carte d'identité du nombre 2016
|
Deux-mille-seize / Two thousand sixteen |
|
|
2 016 = 1 x 25 x 32 x 7 = 2 x 2 x 2 x 2 x 2 x 3 x 3 x
7 |
|
|
1, 2, 3, 4, 6, 7, 8, 9, 12,
14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144,
168, 224, 252, 288, 336, 504, 672, 1008, 2016 |
|
|
36 |
|
|
6 552 |
|
|
S - N |
4 536 > 2 016 => Nombre abondant |
|
111 1110 00002 Suite de
six "1" et cinq "0" |
|
|
Ternaire |
2 202 2003 |
|
Type |
2016 est nombre de Harshad 2016 est triangulaire (n°63) est hexagonal
(n° 32) 2016 est brésilien
(17 fois) |
Amusement avec les facteurs premiers au nombre de huit qui
permet cette symétrie
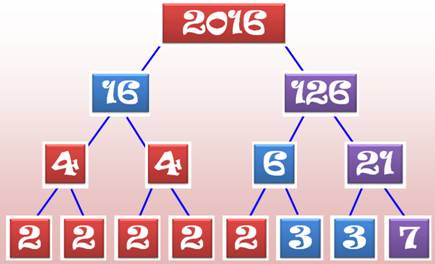
Remarquables
|
|
|
|
|
|
Suite et explications en Jeux
Addition
|
2 016 = 1 + 1001 + 01 + 1 + 10 + 1001 + 1 |
|
|
2 016 = 1 + 2 + 3 … + 63
= T63
= 671 + 672 + 673 = 3 x 672
= 285 + 286 + … + 291 = 220 + 221 + …228
= 86 + 87 + … + 106 = 2 x 32² – 32 = H32 |
|
|
2 016, 6 102, 8 118 |
|
|
2 016 = 64 +
6! = 1 296 + 720 |
|
|
2 016 = 666 +
666 + 666 + 6 + 6 + 6 |
|
|
2 016 = 71 + 73 + … + 157 |
|
|
|
|
Multiplication
|
2 016 = 3 x 2 x 7 x 6 x 8 et 32 768 = 215 |
|
|
|
2 016 = 24 x 84 = 42 x 48 |
|
|
|
|
|
|
|
|
|
|
|
2 016 = ½ 64! / 62! = ½ 64 x 63 |
|
|
|
Sur une idée de Paul
Crowley |
||
|
2 016 = (2 + 0 + 1 + 6)
x 22410
= (1+1+ …0) x 3362
= (2+2+…+ 0) x 2523 etc. |
|
|
|
2 016 = 144 x 14 = 12² x 14 = 12² x (1 + 4 + 9) = 12² + 24² + 36² |
Mais qui permet aussi une somme de carrés. |
|
Puissances
|
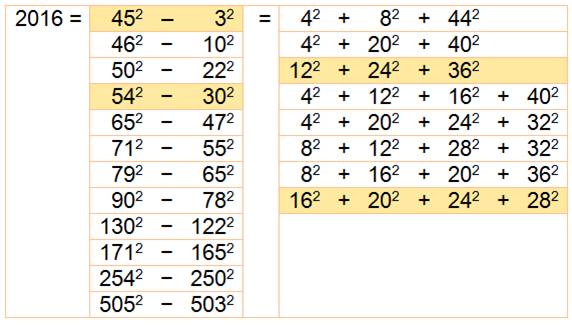
2 016 = 54² – 30² = 45² – 03² |
|
|
2 016 = 26-1
(26 – 1) = 32 x 63 = 25 x (26 –
1) = 26 – 1 + 0 x (26
– 1 + 0) = 211 – 25 =
2048 – 32
|
|
|
2 016 = 12² + 24² + 362 = 16² + 20² + 24² + 28² |
|
|
Somme de carrés
|
|
|
47² + 2 016 =
65² 65² + 2016 = 79² |
|
|
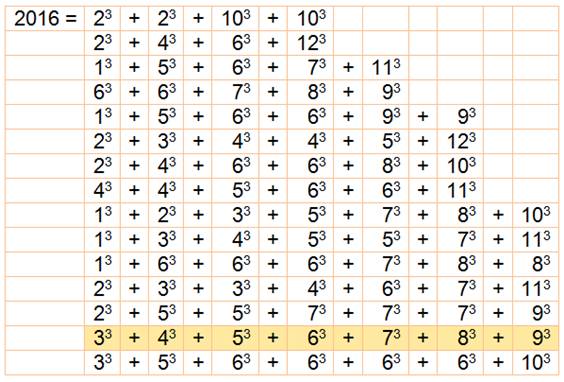
2 016 = 33 + 43
+ 53 + 63 + 73
+ 83 + 93 |
|
|
Somme de cubes
2016 n'est pas somme de puissance 4, 5,
etc. |
|
|
2 016 = 25 + 26
+ 27 + 28 + 29 + 210 |
|
|
2 016² = 4225² – 3713² = 4 064 256 |
|
|
36 = 20 + 16 |
|
|
2 016 = (((((((1 + 2) + 3) + 4)
+ 5) + 6) + 7) x 8 ) x 9 = (10 + 9) x (8 x (7 +
6) ) + 5 x (4 + 3 + 2 – 1)
|
|
|
2 016 = 6! + 3!4
= 720 + 1296 2 016 = ((1 + 2)!)! + 3!4 |
La
première égalité (jaune) donne la clé de la résolution. Valable pour d'autres
nombres autour de 2016. |
|
2 016 = ((1 + 2)!)! + 3!4
= 720 + 1296
= (1 + 2 ) x 3 x 4 x 56 = 36 x 56
= (1 + 2) x ((3!)!) – 4! + 5! = 3 x 720
– 24 – 120 |
|
|
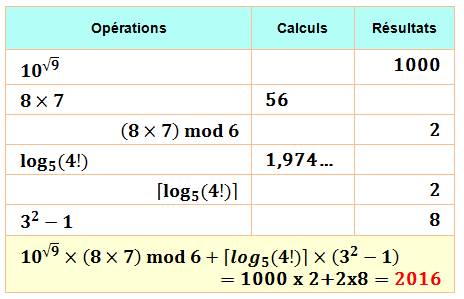
Pourquoi simple, quand
on peut …?
Pour information:
dont la valeur
plafond est 2 (notation: crochets en haut). Voir Factorielle
/ Logarithme
/ Plancher |
|
|
2 016 =
(4 + 4) (44 – 4) = 8 x 252 =
(4 + 4)! / (4! – 4) = 40 320 / 20 =
7 + 7( 7 (7x7 – 7) – 7) = 8x8x (8x8x8 – 8) / (8+8) |
Voir Formule en 2 |
|
2 016 = Q(9–7) |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()