Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 19/02/2025 M'écrire Brèves de Maths

INDEX Polygones Carrés Géométrie Dénombrement Jeux et énigmes	QUADRILATÈRES – Compter
	Quadrilatère	Triangles dans rectangle	Grille & segments
		Angles dans la quadrilatère
	Carré	Triangle dans le carré	Grille & triangles rectangles
		Partage en fils tendus
	Rectangle	Carrés et cercles	Grille & triangles équilatéraux
	Trapèze	Carré (un) dans le carré	Grille & carrés
		CARRÉS dans le carré
	Parallélogramme	Carrés dans rectangle	Rectangle en 3 triangles
	Losange	Rectangles dans carré	Rectangles – Énigmes
	Polygones	Rectangle dans rectangle	Pièce de puzzle
		Quadrilatère dans le carré

Faites un double-clic pour un retour en haut de page

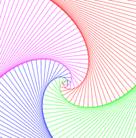
Régions dans le CARRÉ Dénombrement des régions formées dans un carré découpé régulièrement façon fils tendus. Ici, nous sommes dans le cas particulier où toutes les extrémités des fils sont placés sur le périmètre du carré en des points régulièrement espacés.
	Sommaire de cette page >>> Carré divisé avec k = 2 >>> Carré divisé avec k = 3 >>> Carré divisé avec k = 4 >>> Liste des quantités de régions >>> Illustration des cas k = 5 et k = 10	Débutants Nombres Glossaire Nombres

Carré divisé avec k = 2		haut
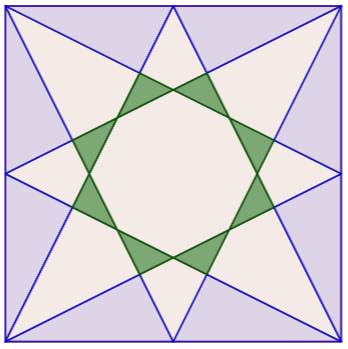
Construction Un carré dont les côtés sont divisés en deux parties égales (k = 2). Un sommet est relié au point milieu opposé. Ces segments découpent le carré en régions. Le but est de compter ces régions. Dénombrement Sur ce cas simple, il facile de compter 25 régions: 3 × 8 = 24 triangles et 1 octogone central.

Carré divisé avec k = 3		haut
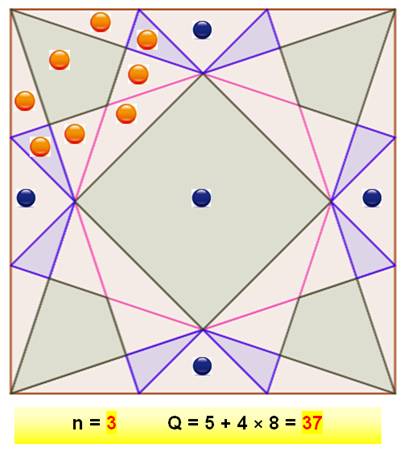
Construction Un carré dont les côtés sont divisés en trois parties égales (k = 3). Chaque point est relié au point quatre pas plus loin (k+1). Ces segments découpent le carré en régions. Le but est de compter ces régions. Dénombrement La figure comporte quatre quarts de carré identiques. Chacun compte 8 régions (8 points orange) En dehors de cela, il existe 5 régions (points bleus). Il ya donc 37 régions.

Carré divisé avec k = 4		haut
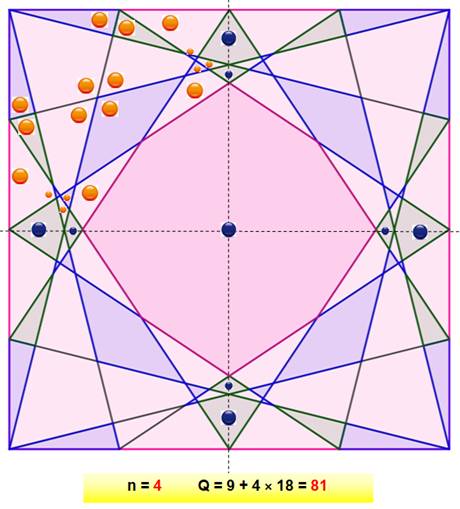
Construction Les côtés du carré sont partagés en quatre parts égales. Dénombrement Même principe avec les points orange et les points bleus. On dénombre 81 régions. Avec k > 4 Il est possible de poursuivre le dénombrement en reproduisant la figure correspondant à k. Cela devient vite fastidieux Formule de calcul Je n'en connais pas et si elle existe elle n'est pas évidente. La progression de la quantité de régions est fortement irrégulière.

Quantité de régions		haut
Liste En commençant par le carré simple, soit k = 1. Pour k = 2, 3 et 4, on retrouve les valeurs citées plu haut: 25, 37 et 81.	4, 25, 37, 81, 109, 169, 205, 289, 341, 441, 485, 625, 701, 825, 913, 1089, 1189, 1369, 1461, 1661, 1805, 2025, 2141, 2389, 2549, 2809, 2929, 3249, 3405, 3721, 3901, 4205, 4421, 4753, 4913, 5329, 5549, 5913, 6105, 6561, 6781, 7225, 7453, 7885, 8189, 8649, …

Illustration des cas k = 5 et k = 10

Images de Lars Blomberg – Accès à d'autres exemples via OEIS

Haut de page (ou double-clic)

	Régions et intersections dans le triangle
Suite	Carré Carrés droits et carrés obliques – Quantité Carrés avec allumettes Carrés dans grille Carrés et rectangles sur l'échiquier Constructions élémentaires: rectangle Quadrilatères – Juniors Rectangles dans le rectangle Triangles dans triangles
Voir	Allumettes Carré Construction à la règle et au compas Dénombrer – Index DicoMot Maths Énigmes classiques Ensembles – les compter Géométrie – Index Jeux – Index Le terrain de basket Losange Rectangles dans le cube Rectangles emboîtés
Sites	OEIS A335350 – a(n) is the number of regions formed in a square by dividing each of its sides into n equal parts – Lars Blomberg
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/Regions.htm