|
Édition du: 01/01/2023 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 100 / 500
/ 1000 / 1500 / 1900 / 2000 / 2016 / 2017 / 2018
/ 2019 / 2020 / 2021 |
2022 |
2023 / 2024 à 2099 / 3000 / 5000 / 10 000 / 20 000 / 50 000 / 100 000 / 106
/ 109 / 10100 Autres |
|
|
Actualités
2022 |
Humour 2022 |
Chiffres de
2022 (jeu) |
Énigmes
2022 |
Faites
un double-clic pour un retour en haut de
page
Carte d'identité du nombre
|
|
|
|||||||||||||||
Suite en propriétés
arithmétiques Voir
Année 2022 |
·
Abondant ·
Composé
·
Fluet · Harshad ou Niven ·
Interpremier
(2017 et 2027) ·
Modeste ·
Pair ·
Pannumérique
en base 5 ·
Semi-parfait
(1011 + 674 + 337) · Sphénique (3 facteurs distincts) |
|||||||||||||||
Chiffres
et Numération
|
2 022 |
·
Nombre avec chiffres 0 et 2
uniquement. Liste autour de 2022: 2000, 2002,
2020, 2022, 2200, 2202 … |
|
|
…,
2013, 2 022, 2031, 2040, … |
·
Années avec somme
des chiffres égale à 6. |
|
|
2 02210 = 22022203 |
·
Nombre qui
est inclus dans son expression en base 3. |
|
|
…, 1124, 1478, 2022, … 112410
= 14789; 147810
= 20229 |
·
Suite de nombres avec procédé
de conversion en base 9. Exemple. |
|
|
2 022 |
·
Nombre holodifférence:
tout chiffre est la différence de deux autres. Tous les nombres avec chiffres (0 et 2) à
partir de 202 le sont. |
|
|
2 022 + 2 202 = 4 224 |
·
Devient palindrome
en lui ajoutant son retourné. |
|
|
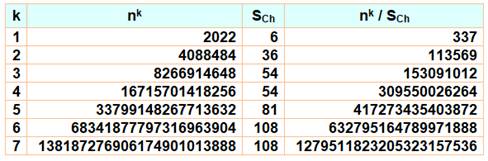
2 022 / (2+0+2+2) =
337 |
·
Nombre Harshad
ou de Niven: divisible par la somme de ses chiffres. Le quotient est un
nombre premier. |
|
|
2022, 2023, 2024, 2025 2022/6 = 337 2023/7 = 289 2024/8 = 253 2025/9 = 225 |
·
Chaine de quatre nombres
Harshad successifs. Évidemment divisibles par des nombres successifs
(6, 7, 8 et 9), somme des chiffres des nombres. Liste: 510, 1014, 2022, 3030, 10
307, 12 102, 12 255, 13 110, … |
|
|
2 + 0 + 2 + 2 = 6 2
+ 3 + 3 + 3 + 7 = 18 = 3 x 6 |
· Nombre
3-Smith: la somme des chiffres divise (par 3) la somme des chiffres de
ses facteurs. |
|
|
2 022 => 20·22 = 4 |
·
Transformation
powertrain
qui finit par 4. |
|
|
|
·
Super-Harshad:
le nombre et ses puissances jusqu'à la septième sont divisibles par la somme
de leurs chiffres. |
|
|
2 022 mod 22 = 20 |
·
Nombre modeste:
divisé par 22 donne 20 pour reste. |
|
|
2 022 mod (2+0+2) = 2 2 022 mod (2+2+2) = 0 |
·
Nombre ModChiffre:
chaque chiffre est égal au nombre mod la somme des autres chiffres. |
|
|
2 022 = 310425 |
· Pannumérique
en base
5. 2022 en d'autres bases >>> |
|
Addition
|
2 022 = 163 + 164 + … + 174 |
· Une
des trois sommes de nombres consécutifs >>> Autre solution facilement trouvable:
ce nombre est divisible par 3: 2022 = 3 x 674;
il est donc somme de 673 + 674 + 675. |
|
|
2 022 = 1009 + 1013 |
· Nombre
sphénique (trois facteurs), somme de deux premiers consécutifs >>> Liste autour de 2022: 1848, 2006, 2022,
2252, 2334, … |
|
|
2 022 = 1011 + 674 + 337 |
·
Nombre semi-parfait:
somme de ses trois plus grands diviseurs. |
|
|
2 022 = T3 + T63 = 6 + 2016 |
·
Somme de deux nombres triangulaires. |
|
|
2 022
|
||
Multiplication,
division
|
2 022 = 6 x 337 |
·
Multiple de 6 dont la somme
des chiffres est 6. Liste autour de 2022: 1500, 2004, 2022,
2040, 2112, … |
|||
|
2 022 = 2 x 674 |
·
Multiple
de 2 avec chiffres de 0 à 2. ·
Multiple
de 3 avec chiffres de 0 à 3. |
|||
|
2022 × 1111 = 1011 × 2222
= 2 246 442 |
·
Curiosité avec les chiffres.
Il en existe d'autre sur ce modèle comme: 2022 x 1101 = 1011 x 2202. |
|||
|
2 022 = 43 x 47 + 1 47
=> 47 x 43 + 1 = 2 022 |
·
Produit
de deux premiers consécutifs + 1. ·
Image de 47 avec la
transformation de
Collatz
généralisé. |
|||
|
2
021, 47, 2 022, 1011, 337, 111548 … ? |
·
Le nombre 2022, image de 47, présente un cycle de Collatz
généralisé long, sans fin ? |
|||
|
2017 + 5 = 2022 = 2027 – 5
|
·
Interpremier:
nombre à égale distance de ses deux voisins premiers. ·
Autre manière de le dire:
2017 est la moyenne
arithmétique entre les deux nombres premiers qui l'encadre. |
|||
|
2
017, 2 022, 2 025,
2027 |
·
Nombre (2022) qui est moyenne des deux premiers
(2017 et 2027) encadrant un carré
(45² = 2025). |
|||
|
|
·
Le nombre 17 581, nombre premier de rang 2022, est
éloigné de 2022 de deux autres nombres
premiers. |
|||
|
2 0223 = 6210 = 2 x 13 2
2023 = 7410 = 2 x 37 |
·
Le nombre comme son retourné
en base 3 sont semi-premiers
lorsque convertis en base 10. Liste: 112, 1021, 1102, 2022, 10111 … A119684 |
|||
|
|
·
Égalité
avec Phi (totient: quantité de nombres premiers avec n) et Sigma (somme
des diviseurs de n) |
|||
|
|
·
La quantité de nombres premiers avec n – Phi(n) – est
un nombre harmonique: la moyenne harmonique
de Phi(n) est un entier. |
|||
Puissance
|
2 022 = 45² – 3 |
· Carré à trois près. Liste autour de 2022: 1846, 1933, 2022,
2113, 2206… |
|
2 022 = 13 + 36 – 41 + 64 |
· Somme de puissances avec même nombres en base et
en exposant – Taneja |
|
2 022² = 4 088 484 2
202² = 4 848 804 |
· Nombre carrément
réversible. Vrai pour 2021. · Nombre fluet:
son carré se calcule sans retenue. · Tous les chiffres sont des puissances de 2: 0, 2,
4, 8. · Famille des nombres dont le premier et le dernier
chiffre du carré est un 4. Voisins: 2018 et 2028. |
|
2 022² = 1 0502 + 17282 =
1 0502 + 1443 =
1 0502 + 126 =
1 0502 + 212 · 36 |
· Somme avec une puissance 6. |
|
2 022² mod 89 = 2 1755, 1805, 1844, 1894, 1933, 1983, 2022, 2072, 2111, 2161, 2200 … |
· Le premier nombre au carré congru à 2 mod 89 est
25. La suite de ces nombres présente une
récurrence: |
Équation 20^x + 22^x = 2022^x
|
Quelles
sont les solutions de l'équation diophantienne: 20x + 22x =
2022x ? Un
raisonnement mod 7 va
révéler qu'il n'y a pas de solution. 20 = 2 x 7
+ 6 => 20 ≡ -1 mod 7 2022 = 288
x 7 + 6 => 2022 ≡ -1 mod 7 En mod 7,
l'équation devient: Le premier
membre vaut 0 ou 2, et le second – 1 ou 1: incompatible! |
Proposé par Brian Sittinger
Jeux et curiosités
|
2 022 = 1234 + 5 – 6 + 789 2 022 = – (1 + 2) + 34 × (– 5 + 6 + 7 + 8 +
9) 2 022 = 9 × 8 × (7 + 6) + 543 × 2 × 1 2 022 = (9 + 8 × (7 × 6 – 5 + 4)) × (3 + 2 + 1) |
· Tous les
chiffres dans l'ordre. |
|||
|
2 022 = – 1 + 2 + 3!4 + 5 + 6!
= 1 + 1296 + 5 + 720 |
· Avec un minimum de chiffres de 1 à n. Solution
de François Lavallou et Alain Zalmanski |
|||
|
2 022 = 69 + 619 + 619 + 619 + 96 2 022 = 8 + 1 + 1 + 1001 + 1001 + 1 + 1 + 8 |
· Sommes palindromes – Taneja |
|||
|
2 022 = 6 + 6 × 6 + 66 × (6 × 6 – 6) |
· Somme avec un seul chiffre – Taneja |
|||
|
…, 1782, 2891, 2002, 2022, 2222, … |
· Appartient à RADD(1,
20): en
partant de 1, retourner le nombre et lui ajouter 20, recommencer. · Appartient
également à RADD(1,
35) |
|||
|
|
· Quelle est la logique de ce tableau ? Le nombre du
bas comptabilise la quantité de
trous dans le nombre du haut. |
|||
|
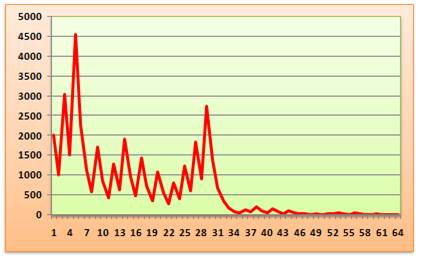
2022, 1011, 3034, 1517, 4552,
2276, 1138, 569, 1708, 854, 427, 1282, 641, 1924, 962, 481, 1444, 722, 361,
1084, 542, 271, 814, 407, 1222, 611, 1834, 917, 2752, 1376, 688, 344, 172,
86, 43, 130, 65, 196, 98, 49, 148, 74, 37, 112, 56, 28, 14, 7, 22, 11, 34,
17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
|
· La suite de
Syracuse pour 2022. |
|||
|
|
· Solutions de cette équation en 2022 ? |
|||
Une belle démo avec des factorielles !
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2022 2,
[1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0] 3,
[2, 2, 0, 2, 2,
2, 0] 4,
[1, 3, 3, 2, 1, 2] 5, [3, 1, 0, 4, 2] 6,
[1, 3, 2, 1, 0] 7,
[5, 6, 1, 6] 8,
[3, 7, 4, 6] 9,
[2, 6, 8, 6] 10,
[2, 0, 2, 2] 11,
[1, 5, 7, 9] |
12,
[1, 2, 0, 6] 13,
[11, 12, 7] 14,
[10, 4, 6] 15,
[8, 14, 12] 16,
[7, 14, 6] 17,
[6, 16, 16] 18, [6, 4, 6] 19,
[5, 11, 8] 20,
[5, 1, 2] 21,
[4, 12, 6] |
22,
[4, 3, 20] 23,
[3, 18, 21] 24,
[3, 12, 6] 25,
[3, 5, 22] 26,
[2, 25, 20] 27,
[2, 20, 24] 28,
[2, 16, 6] 29,
[2, 11, 21] 30,
[2, 7, 12] 60,
[33, 42] |
336,
[6, 6] 673,
[3, 3] 1010,
[2, 2] 2021,
[1, 1] |
Voir Bases / Brésiliens
|
Valeur décimale de 2022 en base b Exemple:
20223 = 6210 |
|||
|
2, 22 3,
62 4,
138 5,
262 |
6,
446 7,
702 8,
1042 9,
1478 |
10, 2022 11,
2686 12,
3482 13, 4422 |
14,
5518 15,
6782 16,
8226 |
|
Retour |
·
Nombre 2021 ·
Nombre 2020 |
|
Suite |
·
Vœux et humour 2022 · Jeu avec
chiffres de 2022 · Nombre 2023 ·
Nombres de 2024 à 2099 ·
Nombres de 2100 à 2299 |
|
Sites |
·
Numbers Aplenty 2022 ·
Année 2022 – Wikipédia ·
Mathematical
Beauty of 2022 - – Inder J. Taneja ·
2020 In Numbers: Mathematical Style – Inder J.
Taneja – Très complet sur les façons de
faire 2020 en opérations de toutes sortes ·
Numbers Magic – Inder. J. Taneja – Nombreux motifs avec les nombres des
années et leurs chiffres |
|
Cette page |