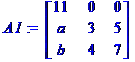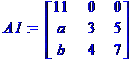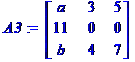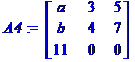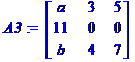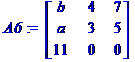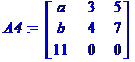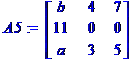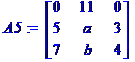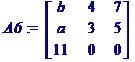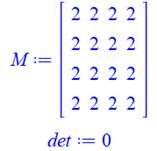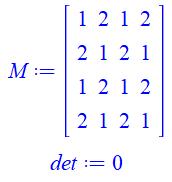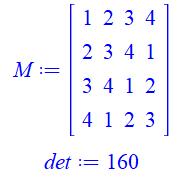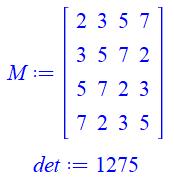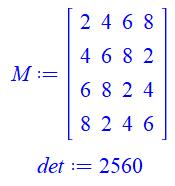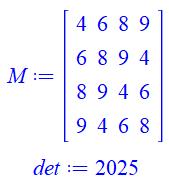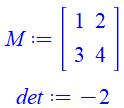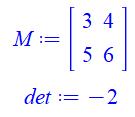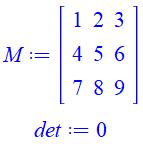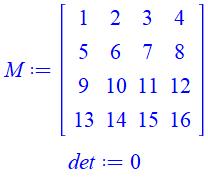NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 30/12/2024

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths    

          

OUTILS

 

Débutants

MATRICE

MATRICES

 

Glossaire

Général

 

 

INDEX

 

Matrices

 

Outils 

 

Introduction

Addition

Multiplication

Puissance

Formes

Déterminant (1/2)

Inversion

Historique

Déterminant (2/2

 

Sommaire de cette page

>>> Simples

>>> Lignes & colonnes

>>> Simplifications

>>> Calcul du déterminant d'une matrice 4×4

>>> Divers déterminants

 

 

 

 

MATRICES – Déterminants (1/2)

 

Le déterminant du deuxième ordre est simple à calculer. Plus fastidieux pour les ordres supérieurs

a

b

c

d

 

D = ad – bc

Voir Débutants / Novices

 

 

Ci-dessous, astuces pratiques pour calculer rapidement le déterminant.

Pour ses applications, voir méthode de résolution des systèmes d'équations linéaires.

 

 

 

Déterminants SIMPLES

 

*      Deuxième ordre

*      Sorte de calcul en croix

 

 

*      Troisième ordre se ramenant au deuxième

 

*      Ce déterminant est la somme de trois déterminants du deuxième ordre multipliés par les coefficients de tête

*      Or deux de ces coefficients sont nuls, il en résulte un seul produit par un déterminant du deuxième ordre

 

3

5

D = 3x7 – 5x4

  = 21 – 20 = 1

4

7

 

 

 

11

0

0

 

 

 

D = 11 x 1

  = 11

a

3

5

= 11

3

5

b

4

7

 

4

7

 

 

11

x

y

 

 

 

D = 11 x 1

  = 11

0

3

5

= 11

3

5

0

4

7

 

4

7

 

 

 

 

 

LIGNES et COLONNES

 

*      Il est parfois pratique d'intervertir des lignes et des colonnes pour faciliter les calculs

Seul le signe du

déterminant change

 

Interversion d'une ligne: changement de signe

Autant d'interversions, autant de changements de signe

 

Exemple: de A1 à A6
A1 à A3 => CS = 1   (-)
A3 à A5 => CS = 2  (+)
A5 à A6 => CS = 3   (-)

Trois changements de signes (CS), soit un résultat négatif

 

Un peu d'explications

Deux phénomènes interviennent dans le changement de signe

1) le déterminant est une somme alternées de produit: le premier terme est positif, le suivant est négatif…C'est le cas lorsque le 11 est en 2e ligne ou en 2e colonne

2) le calcul en croix s'inverse avec certains l'interversion

 

Exemple avec A5

Le 11 est en position négative

Le calcul en croix donne un résultat négatif (5x4 – 7x3)

Le produit est positif

det (A5) = 11

 

 

 

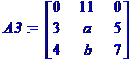
Toutes les interversions (échanges, permutations) de lignes

À pas horizontal ou vertical, une interversion

Déterminant indiqué en rouge

 

  11

- 11

- 11

  11

  11

- 11

 

 

 

Toutes les interversions de colonnes

 

  11

- 11

- 11

  11

  11

- 11

 

 

 

 

 

 

 

SIMPLIFICATIONS  (ordre 3)

 

*      Si deux lignes sont identiques ou si deux colonnes sont identiques le déterminant est nul.

 

 

*      Retrancher une ligne d'une autre ligne ne change pas le déterminant; même chose pour les colonnes.

 

 

*      Il est possible de retrancher plusieurs fois une ligne ou une colonne.

 

 

a

b

c

 0  =

a

a

d

0

a

b

c

b

b

e

d

e

f

c

c

f

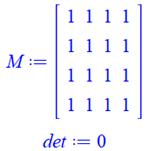
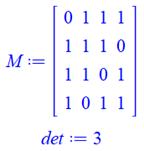
Lignes identiques ou colonnes identiques => det = 0

 

 

5

6

7

 4  =

0

0

1

 4

5

6

6

5

6

6

1

2

3

1

2

3

Première ligne = 1ere – 2e => déterminant simple à calculer

 

 

20

2

0

-2  =

0

2

0

-2

33

3

2

3

3

2

44

4

3

4

4

3

Première colonne = 1ere – 10 x 2e colonne

 

 

 

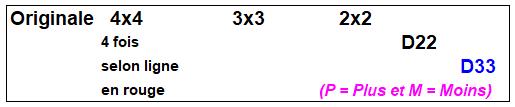
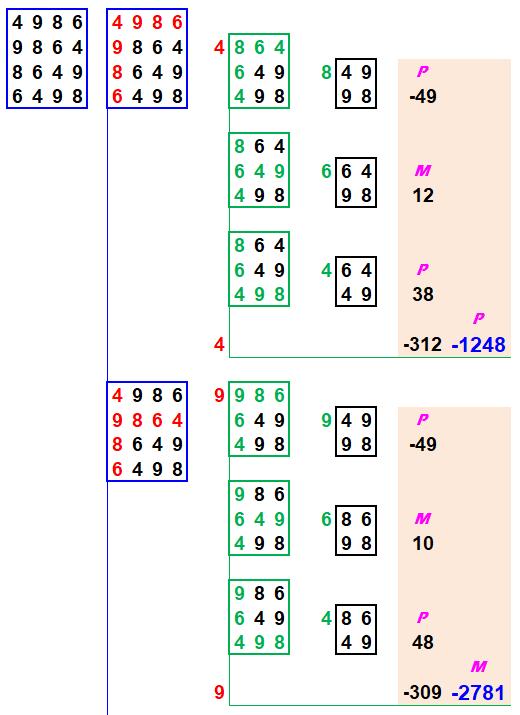
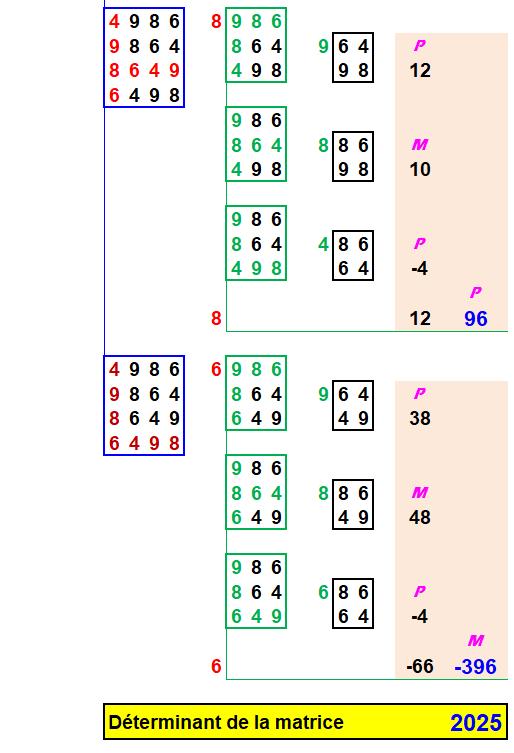
Calcul du déterminant d'une matrice 4×4

haut

 

Méthode de recopie des matrices

La méthode présentée est générale et s'applique à des matrices carrées de toutes tailles.

1)    La matrice originale est recopiée quatre fois.

a.    une colonne est choisie (ici, la une);

b.    une ligne est repérée en rouge pour chacune des matrices.

2)    Pour chacune des matrices 4x4, trois matrices 3x3 sont identifiées selon la même méthode de sélection des lignes-colonnes (en vert).

3)    La même opération est reproduire pour passer des matrices 3x3 aux matrices 2x2.

 

Commentaires

Les lignes et les colonnes dans les matrices intermédiaires (en rouge et en vert) peuvent être choisie autrement; notamment pour faciliter les calculs.

Quelle que soit la matrice, les signes de calcul du déterminant alternent à partir du Plus en haut à gauche.

     

 

Méthode de calcul des déterminants

Tous les déterminants D22 des matrices 2x2 sont calculés: soustraction du produit en croix.
Ex: 4×8 – 9×9 = -49

 

Pour calculer le déterminant D33 d'une matrice 3x3:

1)    Chaque D22 est multiplié par le nombre figurant en tête de ligne sélectionnée (vert)

2)    Le signe est alternativement Plus et Moins en partant de Plus.
Ex: 8(-49) – 6(12) + 4(38) = -312

 

Ce type d'opération est répété pour calculer le déterminant de la matrice complète:

1)    Chaque D33 est multiplié par le nombre figurant en tête de ligne sélectionnée (rouge)

2)    Le signe est alternativement Plus et Moins en partant de Plus.
4(-312) – 9(-309) + 8(12) – 6(-66) = 2025

    

 

Tableau de calcul du déterminant

 

 

Divers déterminants calculés

haut

Avec 0, 1 et 2

 

   

Avec permutations sur les lignes

 

   

Avec nombres premiers; nombres pairs; et, plus petits composés.

 

Avec 1, 2, 3, …

  

 

 

 

 

 

SUITE

*  Déterminants page 2

* Multiplication de matrices

Voir

* Équations

* Outils mathématiques

* Théorie des nombres

Sites

* Matrice (mathématiques) - Wikipédia

* Matrice – Résumé des cours – BibM@th.net

* Matrix -- from Wolfram MathWorld

Cette page

http://villemin.gerard.free.fr/aMaths/Outils/Matrice/Determ1.htm