|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
POINTS et TRIANGLES Trois points non alignés
définissent un triangle. Avec neuf points combien de
triangles? Sous quelles conditions? |
|
|
||
|
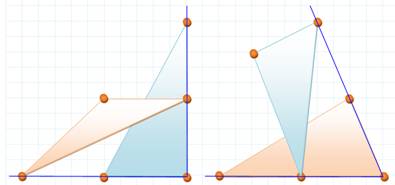
Triangles disjoints
|
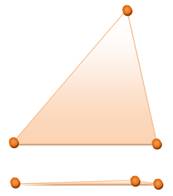
Trois points
Trois points définissent un triangle, sauf si les points sont
colinéaires. Quatre points
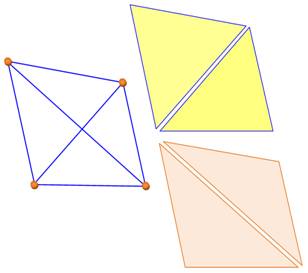
Quatre points définissent quatre triangles qui se juxtaposent ou se
chevauchent. |
|
|
|
||
|
|
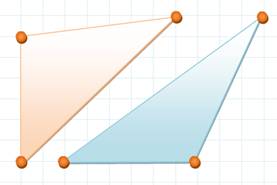
Trois points alignés
Deux triangles distincts avec six points, même si trois sont alignés. Quatre points alignés
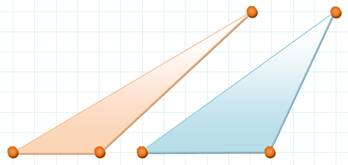
Quatre points alignés sur six permettent encore de dessiner deux
triangles distincts. Double triplets de points alignés
Deux triplets de points alignés avec un point en commun rend
impossible l'obtention de deux triangles distincts. |
|
|
|
||
|
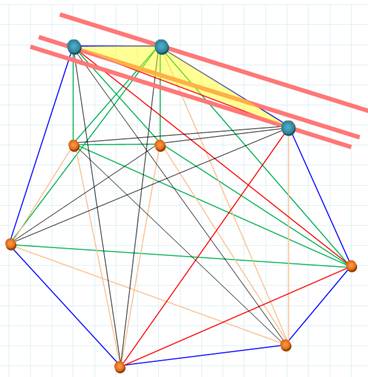
Combien
de triangles distincts peut-on former à coup sûr avec neuf points ne
présentant pas de triplets alignés? Réponse: trois!
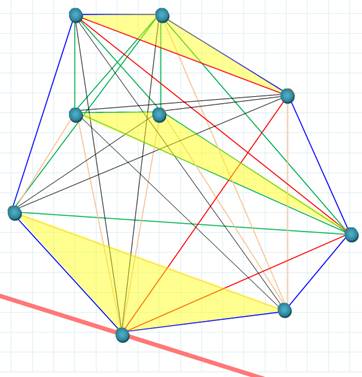
Avec neuf points non-alignés par trois, il est toujours possible de
dessiner trois triangles distincts. Généralisation Avec 3n points non-alignés par
trois, il est toujours possible de dessiner n triangles distincts. Anglais If no three among 3n points are collinear,
then, there exist n disjoint triangles that have those 3n points for their
vertices. P.
Halmos (voir livre cité ci-dessous). |
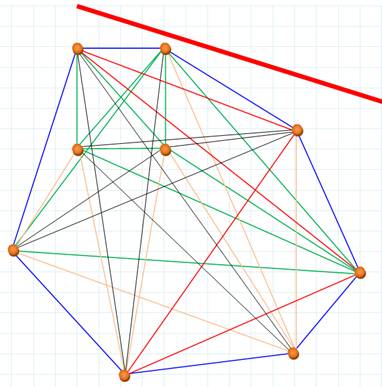
Une droite (rouge) non parallèle aux segments joignant tous les points
deux à deux.
En glissant, cette droite balaye les points les uns après les autres.
Chaque groupe de trois points forment des triangles distincts. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Site |
|
|
Cette
page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Pointtrg.htm |
![]()