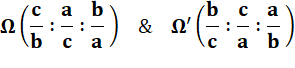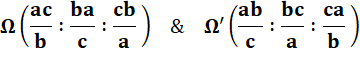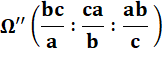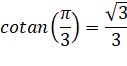NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/07/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
		Quatre triangles	Heilbron	Carrés triangles
		Représentation	Brocard	Cercles et triangles
		Terquem / Gergonne		Démo fallacieuse
		Sommaire de cette page >>> Points de Brocard >>> Construction >>> Cas du triangle équilatéral >>> Cercle de Brocard

Voir Propriétés fondamentales des triangles

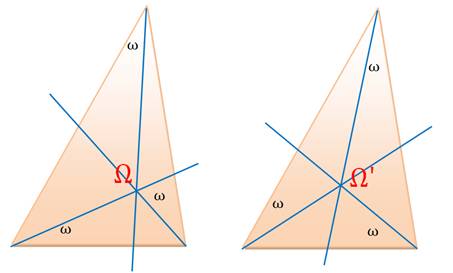
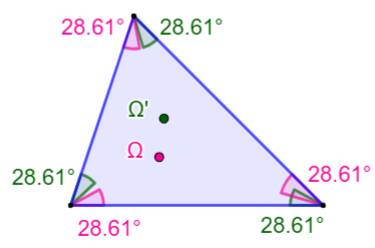
BROCARD

Angle et point / Cercle

Problème: Tracez des céviennes concourantes d'angle constant.

Solution: Ces céviennes sont uniques et leur point de concours est le point de Brocard du triangle.

Cévienne: toute droite issue d'un sommet du triangle

POINTS de BROCARD (1875)
Pour un triangle quelconque, il existe un angle unique , appelé angle de Brocard, tel que les céviennes concourent aux points de Brocard . La valeur de l'angle de Brocard est donnée par la formule indiquée.	Rappel: cotangente = cosinus / sinus
Coordonnées trilinéaires des points de Brocard
Coordonnées barycentriques des points de Brocard Troisième point de Brocard: X(76) de la nomenclature de Kimberling.	Par permutation, on peut créer un troisième point de Brocard:
Propriétés	Les deux points de Brocard sont conjugués isogonaux (symétriques par rapport aux bissectrices). Trois droites concourantes (trois fois par permutations) Médiane par A Symédiane par B Droite de Brocard par C

Voir Points remarquables du triangle

CONSTRUCTION
Tracez les trois cercles passant par deux sommets et tangent à un côté au niveau d'un des sommets (voir figure). Médiatrices des côtés en pointillés roses, et Trois perpendiculaires en chaque sommet aux côtés. En tournant dans un sens ou dans l'autre, on définit l'un ou l'autre des deux points de Brocard.

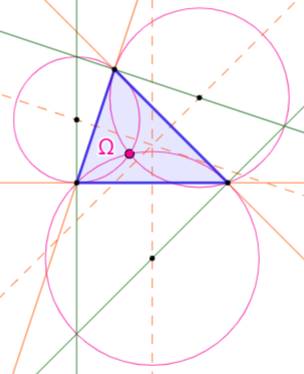
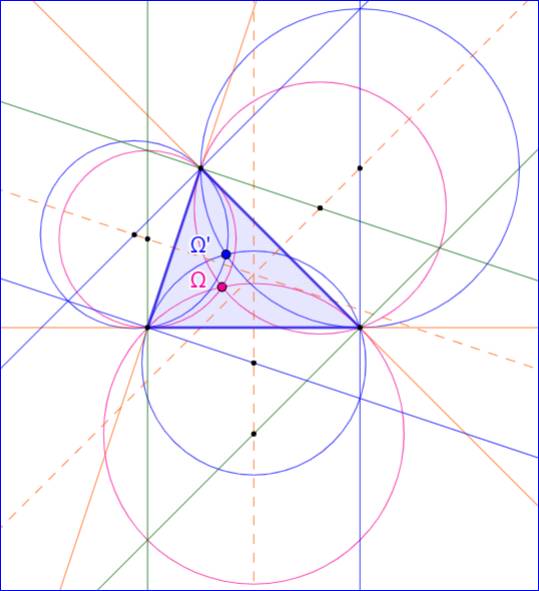
Construction des deux points de Brocard

CAS du triangle équilatéral
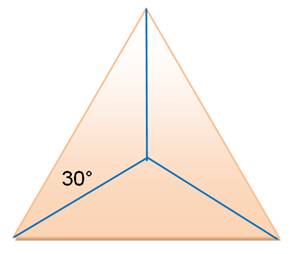
Les angles A, B et C valent 60° ou Quel est l'angle dont la cotangente est trois fois cette valeur	L'angle de Brocard vaut 30° et les deux points de Brocard sont confondus.

Cercle de Brocard ou cercle des sept points
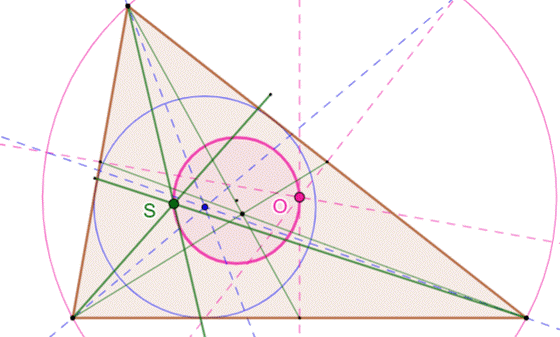
Le point O est le centre du cercle circonscrit. Le point S est le point de Lemoine, point de rencontre des symédianes (symétriques des médianes par rapport aux bissectrices. Le cercle de diamètre OS est le cercle de Brocard.
Cercle des sept points	Le cercle de Brocard passe par: le centre du cercle circonscrit, le point de Lemoine (point symédian) les deux points de Brocard, trois autres pointsde définition pas simple.
Triangle de Brocard	Triangle dont les sommets sont les points d'intersection des hauteurs du triangle initial avec le cercle de Brocard. Voir Point de Steiner

Suite	Droite d'Euler Droite de Simson Points de Terquem / Gergonne
Voir	Triangle – Index Triangle – Glossaire Éléments de géométrie Triangle – Débutants, novices DicoMot DicoNombre
Sites	Point de Brocard – Wikipédia Cercle de Brocard – Wikipédia La géométrie du triangle – Points caractéristiques – Patrice Debart Brocard Points – Wolfram MathWorld Brocard Circle – Wolfram MathWorld ETC X76 Pierre Brocard (1845-1922) – Biographie
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Brocard.htm