Point de Torricelli dans le triangle

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/06/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
		Quatre triangles	Heilbron	Carrés triangles
		Représentation	Brocard	Cercles et triangles
		Terquem / Gergonne		Démo fallacieuse
		Sommaire de cette page >>> POINT DE TORRICELLI ou de FERMAT ou de STEINER >>> CONSTRUCTION

POINT DE TORRICELLI (1608-1647)

ou de FERMAT (1601-1665)

ou de STEINER (1796-1863)

Théorème de Schruttka

Dans tout triangle acutangle ou tout triangle dont aucun des angles n'excède 120°, il y a un point et un seul, tel que les segments qui le relient aux sommets forment entre eux un angle de 120°.

Point de Torricelli

ou de Fermat

C'est le point indiqué ci-dessus; il est tel que la somme des longueurs des 3 segments est minimale.

Anglais: isogonic center

Problème de Fermat

Trouver le point M d'un triangle ABC

tel que AM + BM + CM soit minimum.

Voir Fermat

CONSTRUCTION

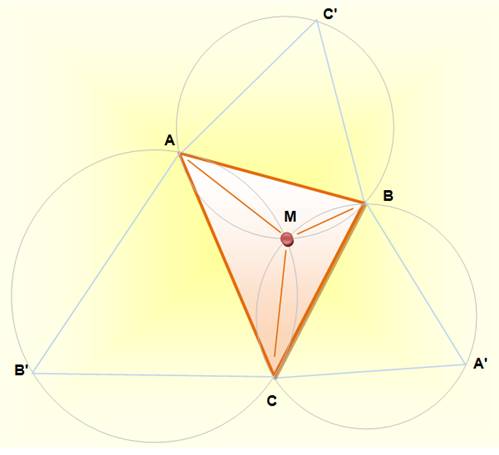
Sur chacun des côtés du triangle, tracez un triangle équilatéral extérieur.

Dessinez le cercle circonscrit à chacun des triangles équilatéraux:

- Ils se coupent en un point unique, le point de Fermat;