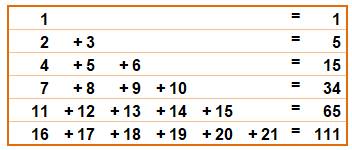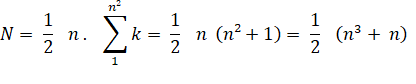NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Généralités				Glossaire Carrés magiques
INDEX Carrés magiques Jeux	Débutant	Introduction	Type	Construction
	Somme magique	Quantité	Dénombrement
	Vocabulaire	Symétrie	Sites
		Sommaire de cette page >>> Calcul de la somme magique >>> Valeurs de la somme magique >>> Constante selon la dimension >>> Carré magique généralisé (décalé) >>> Rappel sur le calcul de la somme des entiers >>> Somme des extrémités des diamètres >>> Propriétés >>> Anglais

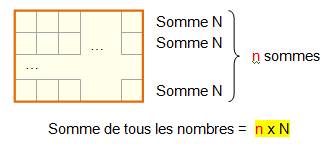
CONSTANTE MAGIQUE

selon l'ordre du carré magique

Il s'agit de faire la somme S de tous les nombres de 1 à n²

si n est l'ordre du carré magique.

Cette somme est répartie à égalité sur n rangées.

Alors, la somme magique N est égale à S / n.

Calcul
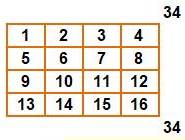
Si n est la quantité de lignes ou la quantité de colonnes ou le côté du carré magique appelé ordre du carré magique. Un carré magique normal utilise tous les nombres de 1 à n². La somme de tous ces nombres placés dans le carré magique vaut S. Or, ces nombres sont répartis sur n lignes, donc, la somme N sur chaque ligne vaut S / n.	Nombres de 1 à n² dans le carré: leur somme S = n x N. Somme des nombres de 1 à n²: S = ½ (n²) (n²+ 1). Somme sur la ligne: N = S / n N = ½ n (n² + 1) = ½ (n^3 + n)

Valeurs de la constante magique
Ordre Somme magique 3 15 4 34 5 65 6 111 7 175 8 260 9 369	10 505 11 671 12 870 13 1105 14 1379 15 1695 16 2056 17 2465 18 2925 19 3439 20 4010
Liste 0, 1, 5, 15, 34, 65, 111, 175, 260, 369, 505, 671, 870, 1105, 1379, 1695, 2056, 2465, 2925, 3439, 4010, 4641, 5335, 6095, 6924, 7825, 8801, 9855, 10990, 12209, 13515, 14911, 16400, 17985, 19669, 21455, 23346, 25345, 27455, 29679, 32020, 34481, 37065, 39775, … OEIS A006003 Ces nombres en ½ n(n² + 1) sont aussi la somme d'un nombre n croissant de nombres successifs comme: Ce sont aussi la somme des nombres entre deux nombres triangulaires successifs, le plus grand compris: Ex: T7 = 28 et T8 = 36 => 29 + 30 + 31 + 32+ 33 + 34 +35 + 36 = 260 Également la somme de trois coefficients binomiaux successifs: Ex: n = 5 => C'est aussi la somme des diagonales du carré des entiers.
Notation mathématiques de la somme magique: Soit, le demi-produit de n par la somme des nombres k pour tous les k de 1 à n au carré. Petite analyse de la progression de cette somme La progression de la constant magique d'un ordre au suivant n'est pas simple. 2Nn = n (n² + 1) 2Nn+1 = (n + 1) ((n + 1)² + 1) 2Nn+1 – 2Nn = (n + 1) ((n + 1)² + 1) – n (n² + 1) Nn+1 – Nn = ½ (3n² + 3n + 2) Progression de deux en deux 2Nn+1 – 2Nn-1 = (n + 1) ((n + 1)² + 1) – (n - 1) ((n - 1)² + 1) Nn+1 – Nn-1 = 3n² + 2 Somme de trois constantes magiques consécutives 2S = (n - 1) ((n - 1)² + 1) + n (n² + 1) + (n + 1) ((n + 1)² + 1) S3 = ½ (3n^3 + 9n)

Voir Somme magique de l'hexagone / Brève 56-1107

Constantes selon la dimension
Carré: S = ½ n (n^2 + 1) Cube S = ½ n (n^3 + 1) Hypercube S = ½ n (n^4 + 1) Dimension d S = ½ n (n^d + 1)

Carré magique généralisé (décalé)

Carrés magiques avec

un premier nombre égal au premier nombre classique (1) et un supplément de a, soit 1 + a , et

une progression régulière de r pour les suivants.

Rappel: le A inversé veut dire quelconque.

Exemple 1: a = 10 et r = 3 pour un carré 3x3

	6	1	8	15			16	11	18	45
	7	5	3	15	+10		17	15	13	45
	2	9	4	15			12	19	14	45
15	15	15	15	15		45	45	45	45	45
					+10		28	13	34	75
					x 3		31	25	19	75
							16	37	22	75
						75	75	75	75	75

Départ: carré magique d'ordre 3, constante 15

Plus 10 sur chaque terme, constante 15 + 3 x 10 = 45

Trois fois chaque terme plus 10, constante 3 x 15 + 3 x 10 = 75

Exemple 3: a = 3 et r = 5

Chaque nombre t du carré classique devient T = 5t + 3 (fonction linéaire)

6	1	8	33	8	43
7	5	3	38	28	18
2	9	4	13	48	23

Départ: carré magique d'ordre 3, constante 15.

n fois 5 sur chaque terme, plus 3.

Nouveau carré magique avec les nombres allant

de 8 = 1 x 5 + 3
à 48 = 9 x 5 + 3

Sa somme magique vaut: 84, trois fois le terme central 28.

Il reste associatif de somme 56, deux fois le terme central.

Calcul

Les nombres sont en progression arithmétique.

Ils commencent par D = r + a Ici: 5 + 3 = 8, et

Ils finissent par r. n² + a Ici: 5 x 9 + 3 = 48.

La somme des nombres d'une progression arithmétique vaut le demi-produit de la quantité de termes Rappel: c'est n² par la somme des extrémités, début et fin: S = ½ n² (D + F).

Cette somme est répartie à égalité sur n rangées, soit la somme magique pour une rangée: N = S / n.

D'où la formule finale:

N = ½ n [ r + a + r . n² + a ]

N = ½ n [ 2a + r (n² + 1) ]

N = ½ r.n(n² + 1) + n.a

Ici: ½ 3 (2 x 3 + 5 (3² + 1) ) = ½ 3 (6 + 50) = 84.

2016 – Exemple d'application

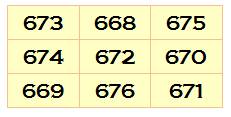
Comment trouver un carré magique 3x3 avec des nombres successifs dont la constante magique est 2016.

La somme vaut: 2016 = ½ 3 (9 + 1) + 3a = 3a + 15

Ou encore: 2016 = 3 x 672 = 3a + 3 x 5

Soit la valeur: a = 672 – 5 = 667.

Et le nombre initial: a + 1 = 668

Voir Nombre et année 2016

Rappel

Calcul de la somme des nombres

Pour calculer cette somme simplement, on procède comme Gauss lorsqu'il était encore enfant, on ajoute les chiffres deux par deux de la manière indiquée.

Voici l'exemple pour les nombres de 1 à 9:

1								+9	= 10
	+2						+8		= 10
		+3				+7			= 10
			+4		+6				= 10
				+5					= 5
1	+2	+3	+4	+5	+6	+7	+8	+9	= 45

Voir Nombre triangulaires

Somme des extrémités des diamètres

Pour certains carrés magiques, la somme des deux nombres à l'extrémité d'une ligne, colonne ou diagonale est constante.

Elle est égale au double du nombre central, qui est aussi la somme des plus petits et plus grands nombres utilisés (n² + 1).

Ces carrés sont dits ASSOCIATIFS.

Cas du carré classique d'ordre 3

6	1	8
7	5	3
2	9	4

6	+	4	=	10
7	+	3	=	10
8	+	2	=	10
1	+	9	=	10
5	x	2	=	10

Propriétés
Carré associatif d'ordre impair La somme de deux termes diamétralement opposés vaut la somme des deux nombres extrêmes: n² + 1. Le terme central vaut la moitié de cette somme.

ENGLISH CORNER
Magic constant or magic sum: the sum produced by addition of all numbers on a row, or a column or a diagonal.

Suite	Sommes magiques pour carrés magiques premiers Carrés magiques – Débutants Carrés magiques – Introduction Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie Humour Jeux Jeux de chiffres Magie – Index Nombres magiques - Index Pannumérique Rubriques débutants Sommes Sudoku Propriétés du carré magique
Diconombre	Nombre 3 Nombre 15 Nombre 34
Sites	Pour beaucoup plus: voir le site de Harvey Heinz   Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/Somme.htm