|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
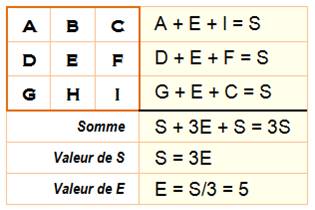
Carré magique 3 x 3 dit d'ordre 3 Formules mathématiques et
programmation. |
|
|
|
|
2 x 6 = 9 + 3; 2 x 8 = 7 + 9; 2 x 2 = 1 + 4 et 2 x 4 =
7 + 1.
6² + 7² + 2² = 8² + 3² + 4² = 89 6² + 1² + 8² = 2² + 9² + 4² = 101 |
|
|
des carrés magiques d'ordre 3 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Nous
savons que l'élément central est fixé (5) et la somme
de deux nombres opposés est toujours 10. Formules
simples
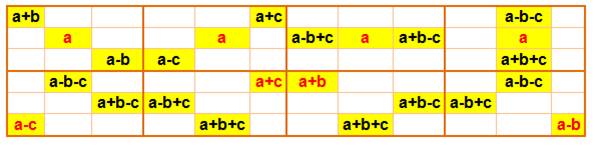
Formules
générales dues à Édouard Lucas
Voir Démonstration
Remarque: avec a, b et c quelconque,
on n'est pas assuré d'avoir des nombres différents ou consécutifs.
Voir Exploitation
de cette propriété (parallélogramme magique) / Programmation
des carrés alpha-magiques Quelques
exemples utilisant la forme générique Le
classique avec les nombres de 0 à 9
En
voici trois autres |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Voir Propriétés des
carrés 3 x 3 / Construction du carré 9x9
|
|
||||||||||||||||||||||||||||
|
Carré
normalisé
Autre
forme générique
Semi – magique
|
||||||||||||||||||||||||||||
|
|
||
|
Nous nous
proposons de construire les huit carrés magiques permutés d'ordre 3. Il s'agit
plutôt d'un exercice de programmation
avec les tableaux de nombres
(matrices). Méthode valable seulement pour les petits carrés magiques. Voir Programmation pour les grands carrés Exercice, car cette programmation permet de se
familiariser avec la manipulation des matrices qui recèle quelques pièges. |
Oups ! Pour un carré 3x3, il y a 9! = 362
880 permutations
des neuf nombres à analyser. Il y en aurait déjà 21 mille milliards (20 922
789 888 000) pour l'ordre 4 |
|
|
|
Commentaires Réinitialisation (restart).
Appel des logiciels de traitement des matrices (ArrayTools)
et de combinatoire. Formation d'une matrice (2x4) pour y loger nos
huit carrés magiques. La liste e des
nombres de 1 à 9 est permutée en E. Pour chaque permutation f, on forme la matrice A. Puis on calcule la somme en colonnes avec AddlongDimension et le paramètre 1, puis la
somme en lignes avec le paramètre 2. Pour les diagonales, on additionne les éléments
de même indice pour l'une et d'indices complémentaires pour l'autre. SC est l'ensemble
(set) des sommes sur les colonnes. Si les
sommes sont identiques, l'ensemble ne comporte qu'un seul élément (nops = 1). Si en plus, les sommes en diagonales valent 15,
alors le carré est magique. Les carrés magiques sont alors rangés dans un
super tableau selon la valeur de leur rang (kt).
Voir le Explication du calcul
de i et j |
|
Voir Programmation – Index / Brève
481
![]()
|
Suite |
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
Cette page |
||
![]()