collection de nombres, carrés magiques, ordre 4

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/11/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Carré magique 4 x 4					Glossaire Carrés magiques
INDEX Carrés magiques Ordres Constructions Magie Jeux de grilles Jeux et énigmes	Carré 4 x 4	Décompte		Formules		Premiers
	Carré mental	Propriétés		Relations		Pandiagonaux
	Plus que parfait	Classement		Cousinage		Franklin
	Réversible	Alpha-magique				Étude de cas
	Dürer – Mélancolie		Subirach – Sagrada Familia		Romain LV
		Sommaire de cette page >>> Carré magique d'ordre 4 >>> Construction d'un carré 4 x4 >>> Construction de De la Hire >>> Exemples >>> Propriétés >>> Amusement décimal >>> Nombres au carré et au cube >>> Carré du temple de Khajuraho >>> Avec des nombres premiers >>> Deux carrés inversés >>> Nombres réversibles >>> Nombres doublonnés

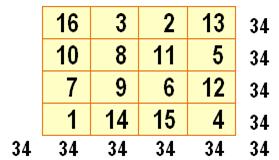
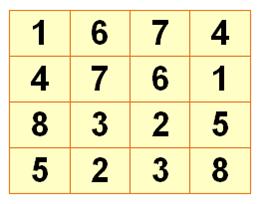
Carré magique 4 x 4

dit d'ordre 4

Ils sont nombreux: 880 dont 48 plus que parfaits. Et, pourtant, pas si facile que cela à construire.

Carré magique de Dürer

Deux principales sortes de carrés magiques 4 x 4:

les carrés quelconques (ou simples):
la somme magique est répétées 10 fois: lignes, colonnes et diagonales principales; et

les carrés plus que parfaits (PQP):
la somme magique s'y retrouve 32 fois: diagonales secondaires (pandiagonales) et tous les carrés 2x2.

CARRÉ MAGIQUE d'ordre 4
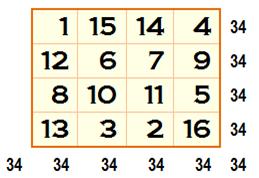
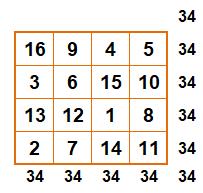
Définition Un carré magique d'ordre 4 s'inscrit dans une grille de 16 cases dans laquelle, les nombres 1 à 16 sont placés pour obtenir la même somme des quatre nombres sur chaque ligne, sur chaque colonne et sur chaque diagonale.	Une variante du carré magique de Dürer montré ci-dessus.
Somme magique (m) Somme (S) de tous les nombres de 1 à 16 Voir Formule Somme de tous les nombres dans le carré: Évaluation possible en prenant la somme des quatre lignes ou celle des quatre colonnes.	S = 1 + 2 + 3 + … + 16 = 16 x 17 / 2 = 136 S = 4 m = 136 m = 136 / 4 = 34 La somme magique pour l'ordre 4 est 34.

Quantités de sommes

Avec les nombres de 1 à 16, pris par quatre (1820 combinaisons), il est possible de former 86 fois la somme magique de 34.

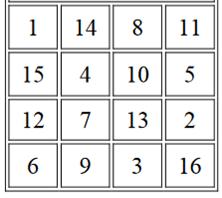
Un carré magique voisin

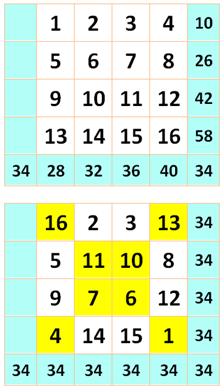
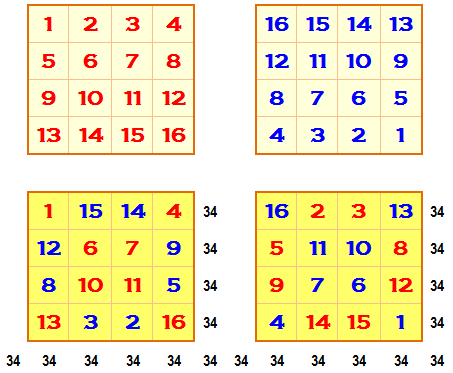
Construction d'un CM d'ordre 4 – Exemple
La construction la plus simple en deux étapes: lister les nombres de 1 à 16 dans les cellules du carré; et inverser chacune des grandes diagonales (jaune). Autre manière de voir: les nombres en décomptant de 16 à 1 sont inscrits lorsqu'ils sont sur les diagonales, et les nombres en comptant de 1 à 16 remplissent les cases vides. Ce carré est bien magique. Par contre, il n'est: ni panmagique: Ex: 2 + 10 + 12 + 4 = 28. Quatre diagonales sur 8 somment en 34. Celles qui commencent en 16, 3, 4 et 15. ni plus que parfait: Ex: 2 + 3 + 11 + 10 = 26. Huit carrés 2x2 sur 16 somment en 34. Ce sont ceux avec sommets en (avec enroulement si nécessaire):16, 3, 11, 8, 9, 6, 14, 1.		Carré magique 4 x 4 simple Voir Carré de Dürer
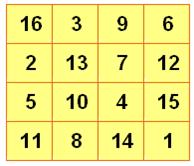
Transformations En divisant le carré magique en quatre carrés 2x2, la somme des quatre nombres est magique: Ex: 16 + 2 + 5 + 11 = 34. Cette propriété est propice à la confection d'un nouveau carré magique en plaçant chacun de ces quatre nombres sur une colonne.		Même carré que ci-dessus, mais avec carrés 2x2 devenus colonnes
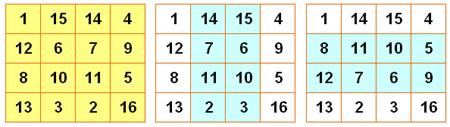
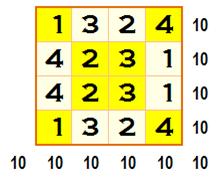
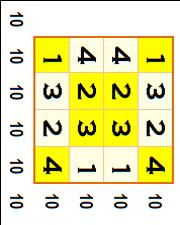
Permutations Ce carré (jaune) reste magique en inversant les colonnes et ou les lignes.

Voir Construction d'un CM d'ordre 8

Cette méthode en bref

Deux carrés: l'un avec les nombres successifs, l'autre à l'envers. Les diagonales sont sélectionnées dans l'un et complétées par les nombres de l'autre. Les deux carrés magiques obtenus sont symétriques.

Construction de De la Hire
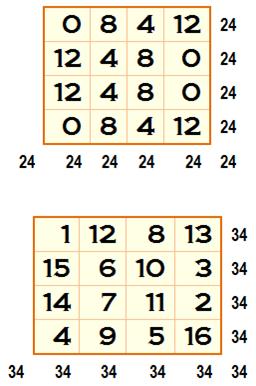
Méthode utilisant deux carrés auxiliaires (méthode matricielle). Généralisable aux carrés d'ordre pair.
Le premier carré est rempli avec les nombres de 1 à 4: les deux diagonales avec les quatre nombres, puis les cases latérales de manière à former un carré magique de somme 10. Un deuxième correspond au premier retourné de 90° Un troisième carré est formé en prenant 4 fois les nombres diminué de 4. Le carré magique est obtenu en sommant les cases correspondantes est carrés 2 et 3.	Carrés 1 et 2 Deux carrés latins orthogonaux: tous les couples sont présents et ne se répètent jamais.	Carrés 3 et 4 Le carré magique est associatif: la somme de deux sommets symétriques par rapport au centre est constante.
En prenant le carré 2 pour faire le 3, on obtient un second carré magique associatif, semblable au premier. Il est, lui aussi, associatif.

Quelques exemples

Exemples de carrés magiques d'ordre 4

1	12	8	13
6	15	3	10
11	2	14	7
16	5	9	4

1	14	8	11
7	12	2	13
10	5	15	4
16	3	9	6

1	16	11	6
13	4	7	10
8	9	14	3
12	5	2	15

1	15	8	10
4	14	5	11
13	3	12	6
16	2	9	7

Carré associatif:

La somme des nombres opposés = 17

1	14	15	4
8	11	10	5
12	7	6	9
13	2	3	16

Carré miroir:

La somme des nombres miroir vertical = 17

1	11	6	16
14	13	4	3
7	2	15	10
12	8	9	5

Carré avec toutes des demi-diagonales = 17

1	7	14	12
10	16	5	3
15	9	4	6
8	2	11	13

Dix autres exemples, voisins du carré magique de Dürer

avec 1514 ou 1415 en bas du carré, 1514 étant la date de réalisation d'un tableau par Dürer.

Obtenus avec le logiciel Maple

Voir Autres exemples en classement

PROPRIÉTÉS

Bernard Frénicle de Bessy a montré (en 1640, publication 1693) qu'il y avait 880 carrés magiques d'ordre 4. On parle bien des carrés magiques normaux, ceux utilisant tous les nombres de 1 à 16.

Identification des propriétés des carrés magique 4x4 >>>

Propriétés des carrés magiques selon leur type >>>

Amusement décimal
C'est normal! Prenons un carré magique 4 x 4. Nous formons de nouveaux nombres en prenant 10 fois une colonne plus la colonne suivante. La somme de ces nouvelles colonnes est égale à 374 = 11 x 34. C'est normal: nous avons fait dix fois la somme d'une colonne plus la colonne suivante, soit onze fois la somme magique. Évidemment, cette propriété est valable pour toute ligne, colonne, dans un sens ou dans l'autre.
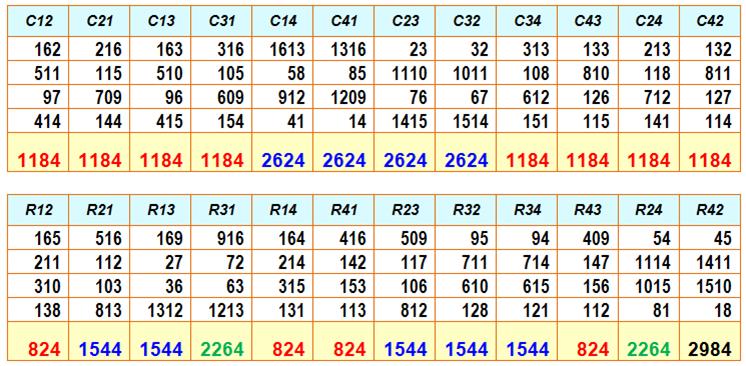
Ah! Pas si banal … Nous faisons la même chose mais en concaténant les nombres: par exemple 5 et 11 deviennent 511 (en non 10x5 + 11 = 61). Une petite précaution, si le neuf est à droite on le prend comme 09. Observons les sommes: Les sommes en colonne se classent en deux catégories: 1184 = 32 x 37 ou 2624 = 64 x 41. Celles en rangées en quatre catégories: 824 = 8 x 103 ou 1544 = 8 x 193 ou 2264 = 8 x 283 ou encore 2984 = 8 x 273). 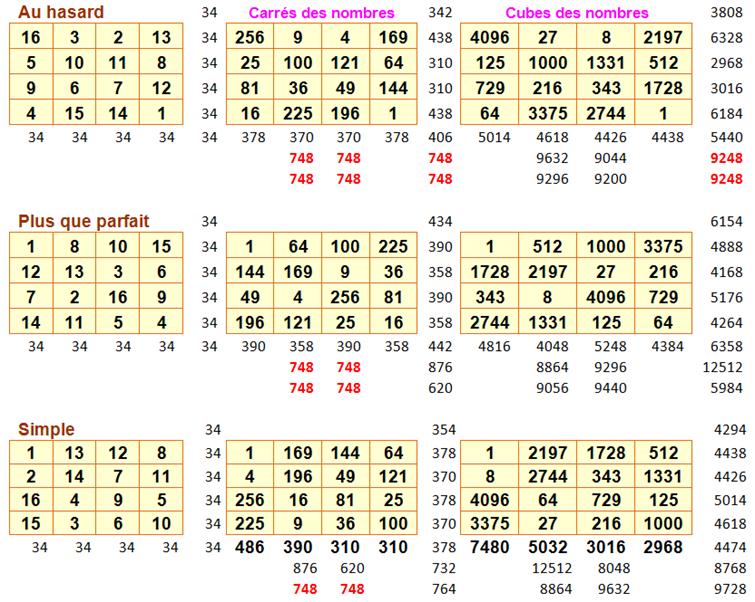Conclusion: La concaténation des colonnes conduit à deux catégories de totaux seulement; celle des rangées est un peu moins centrée avec quatre sortes de totaux. La valeur des totaux sont divisible par une puissance de 2 (au moins 8 = 2³) et par un nombre premier toujours assez grand.

Nombres au carré et au cube
En partant d'un carré magique, créons les carrés avec les mêmes nombres au carré, puis les nombres au cube. Quelles sont les propriétés de ces nouveaux carrés? Trois types de carrés magiques 4x4 Le carré du haut, un voisin du carré de Dürer, avec ses cousins sont tels que: Carrés Somme colonne 1 = celle de 4 = 378 Somme colonne 2 = celle de 3 = 370 Somme ligne 1 = celle de 4 = 438 Somme ligne 2 = celle de 3 = 310 Somme partie droite = celle de partie gauche = celle du haut = celle du bas = 1/2 somme des chiffres du carré = celle des deux diagonales = celle des hors diagonales = 748 (en rouge) Cubes Somme des deux diagonales (8 nombres) = celle des hors diagonales (en rouge). Conclusion de nos observations Le carré du haut avec ses carrés et ses cubes présentent des propriétés intéressantes. Hélas, même les carrés plus que parfaits (groupe 1) ne répondent pas à ces propriétés et encore moins les carrés les plus simples (groupe 12)
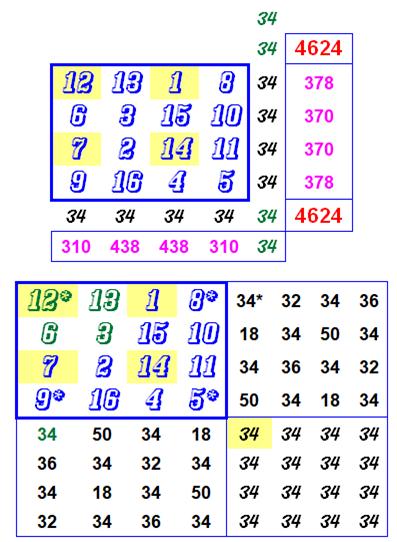
Carré singulier avec carrés et cubes (partiels) Carré magique avec somme 34. Les secondes pandiagonales font 34. Les sommes de paires de nombres en "rayons" sont toutes égales à 17, y compris les deux centraux (Carré associatif complet). La somme des cubes des diagonales forment un carré 4 624 = 68² La somme des carrés des lignes et colonnes forment des couples de même valeur: 378, 370, 310 et 438. Tableau du bas: On retrouve la somme magique en sommant quatre nombres sur des fenêtres glissantes (imaginez le carré magique répété formant un tapis continu). 34 partout pour la somme des quatre éclairés en jaune *34 pour la moitié d'entre eux pour les sommes avec aux quatre coins () 34 pour la moitié d'entre eux pour les sommes avec quatre en petit carré (vert).**

Propriétés sur carrés et cubes d'après Allan Adler

Voir Carré presque magique avec des nombres au carré

Carré du temple de Khajuraho (Inde)

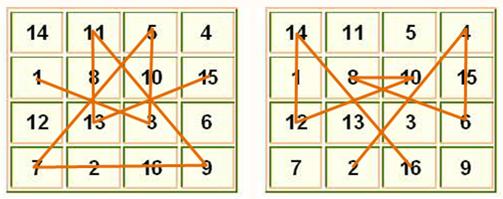
C'est sans doute le plus ancien carré magique (X^è ou XI^è siècle).

7	12	1	14
2	13	8	11
16	3	10	5
9	6	15	4

Carré magique Chautisa Yantra, datant du 10^e siècle

et figurant dans un temple Jain en Inde.

C'est un carré magique pandiagonal. En plus, la plupart des carrés de 4 cases forment aussi la somme magique:

7+12+2+13 = 2+13+16+3=...= 7+14+9+4 =...= 34

De même pour les coins des carrés 3 x3.

Ce carré est plus que parfait

Pour l'amusement, le trajet des nombres impairs et celui des nombres pairs dans ce carré (retourné de 90°):

Carré magique,

probablement du XV^e siècle, retrouvé dans les ruines d'un temple à Gwalior en Inde.

AVEC DES NOMBRES PREMIERS

On peut construire 3 carrés magiques, dont 2 avec les mêmes nombres, en utilisant les nombres premiers consécutifs inférieurs à 200. Ici avec somme 258:

101	47	31	79
73	61	71	53
43	67	59	89
41	83	97	37

Suite en Carrés magiques avec des premiers

Deux carrés inversés

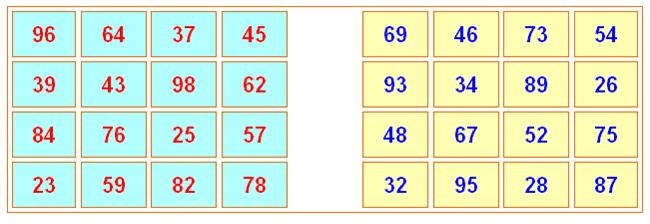
Deux carrés d'ordre 4, somme 242 y compris pandiagonales.

Les nombres de l'un sont les inversés de l'autre.

Nombres réversibles

– Carré ambi-numérique

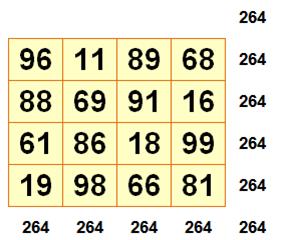
Tous les nombres de ce carré magiques peuvent être retournés.

Nombres utilisés: 11, 16, 18, 19, 61, 66, 68, 69, 81, 86, 88, 89, 91, 96, 98 et 99.

De nombreuses sommes de quatre chiffres donnent 264 dont les quatre coins, le centre, les carrés 2x2 des coin, etc.

Voir Autre présentation

Nombres doublonnés

Nombres de 1 à 8, deux fois.

Somme égale 18.
Aucun identiques sur lignes, colonnes, diagonales, quatre carrés 2x2 de coins, carré central et carré des quatre coins.

Ce carré est en fait le carré de Dürer; les nombres au-delà de 8 sont diminués de 8. Il en a toutes les propriétés.

Suite	Carré diabolique de Dürer Carré de la Sainte Famille Exemple de calcul sur un carré 4 x 4 Carré 4 x 4 en cercles Carré 5 x 5 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie Humour Jeux Jeux de chiffres Nombres consécutifs Nombres magiques - Index Pannumérique Rubriques débutants Sudoku Propriétés du carré magique
Diconombre	Nombre 3 Nombre 15 Nombre 34
Sites	Liens vers les sites carrés magiques Order 4 Magic Squares – Harvey Heinz – Plus que complet, y compris la liste des 880 carrés magiques.
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordre4.htm

Renvois de liens

DIABOLIQUES – Exemple: Carré de Dürer >>>

CARRÉ PANDIAGONAL >>>

TOUS LES CARRÉS PANDIAGONAUX D'ORDRE 4 >>>

FORMULES GÉNÉRIQUES POUR LE CARRÉ D'ORDRE 4 >>>

BI-MAGIQUE D'ORDRE 4 >>>

CARRÉ MAGIQUE À TROU >>>