|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres de SMITH Nombre tel que la somme de ses
chiffres est égale à la somme des chiffres de ses facteurs: SCHIFFRES (n) = SFACTEURS
(n) Ex: 319 = 11 x 29 et 3 + 1 + 9 = 1 + 1 +
2 + 9 = 13 |
|
|
||
|
Approche Un
nombre: la somme de ses chiffres. Ses
facteurs: la somme des chiffres de ses facteurs. Si
égalité => nombre de Smith L'universitaire
Albert Wilansky a remarqué un jour que le numéro de téléphone de son
beau-frère Harold Smith avait cette propriété. |
22 => 4 2
x 11 => 4 |
|
|
Définition Nombre dont la somme des chiffres
est égale à la somme de tous les chiffres de ses facteurs premiers. |
En c |
|
|
Jumeaux Il existe
des nombres consécutifs qui sont des nombres de Smith: Smith jumeaux (Smith
brothers). On ne connaît pas leur dénombrement. |
Exemples 728
et 729 2 964
et 2 965 |
|
|
Exemples |
666 = 2 x 3 x 3 x 37 6 +
6 + 6 = 18 2 +
3 + 3 + 3 + 7 = 18 1776
= 2 × 2 × 2 × 2 × 3 × 37 1 +
7 + 7 + 6 = 21 1+7+7+6=2+2+2=2+3+3+7=21 |
6 036
= 2 x 2 x 3 x 503 6 +
0 + 3 + 6 = 15 2 +
2 + 3 + 5 + 0 + 3 = 15 4
937 775 = 3 x 5 x 5 x 65 837 4+9+3+7+7+7+5
= 42 3+5+5+6+5+8+3+7
= 42 |
|
Propriétés |
Tous les
nombres premiers sont des nombres de Smith triviaux et sont exclus de la liste. Il est
prouvé qu'ils sont en nombre infini.
6 jusqu'à 100
49 jusqu'à 1000
376 jusqu'à 10 000 29 928 jusqu'à
1 million Si p est
un premier repunit alors 3304p
est un nombre de Smith. |
|
|
Anglais |
Smith number or joke numbers The sum of its
digits is equal to the sum of the digits in its factorization |
|
|
|
||
|
Nombre de Smith (somme de
tous les facteurs)
4, 22, 27,
58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 378, 382, 391, 438, 454, 483, 517, 526, 535, 562, 576, 588, 627, 634, 636, 645, 648, 654, 663,
666, 690, 706, 728, 729, 762, 778, 825, 852, 861, 895, 913, 915, 922, 958, 985, 1086 … |
Nombre de Smith réduit (somme
des facteurs uniques) 84, {2, 3, 7}, 12
(84 = 2² x 3 x 7) 160, {2, 5}, 7 250, {2, 5}, 7 336, {2, 3, 7}, 12 468, {2, 3, 13}, 18 735, {3, 5, 7}, 15 936, {2, 3, 13}, 18 975, {3, 5, 13}, 21 |
|
Plus petit carré magique avec des nombres de Smith
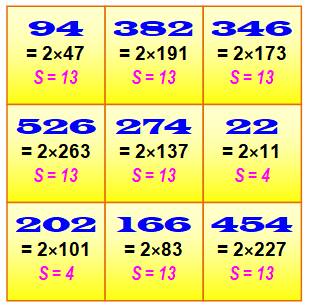
Voir Carrés magiques 3x3
|
Nombre de Smith (variante) Somme des chiffres = somme des facteurs (et non des chiffres des facteurs), et
cela avec leur multiplicité. |
N,
Chiffres, Facteurs, Sommes 27, [7, 2], [3, 3, 3], 9, 9 378, [8, 7, 3], [2, 3,
3, 3, 7], 18, 18 576, [6, 7, 5], [2, 2, 2,
2, 2, 2, 3, 3], 18, 18 588, [8, 8, 5], [2, 2, 3,
7, 7], 21, 21 648, [8, 4, 6], [2, 2, 2,
3, 3, 3, 3], 18, 18 729, [9, 2, 7], [3, 3, 3, 3, 3,
3], 18, 18 2688, [8, 8, 6, 2], [2, 2, 2, 2, 2,
2, 2, 3, 7], 24, 24 17496, [6, 9, 4, 7, 1], [2, 2, 2, 3,
3, 3, 3, 3, 3, 3], 27, 27 19683, [3, 8, 6, 9, 1], [3, 3, 3, 3,
3, 3, 3, 3, 3], 27, 27 49896, [6, 9, 8, 9, 4], [2, 2, 2, 3,
3, 3, 3, 7, 11], 36, 36 69888, [8, 8, 8, 9, 6], [2, 2, 2, 2,
2, 2, 2, 2, 3, 7, 13], 39, 39 |
|
|
Liste |
27, 378, 576, 588,
648, 729, 2688, 17496, 19683, 49896, 69888, … |
|
|
|
||
|
Nombres
dont la somme des chiffres divise deux fois la somme des chiffres des
facteurs. Facteurs
comptés une fois. |
42, 70, 212, 231, 322, 330, 406,
430, 602, 610, 700, 703, 1004, 1027, 1032, 1071, 1162, 1190, 1206, 1246,
1261, 1320, 1351, 1406, 1510, 1530, 1603, 2012, 2013, 2054, 2065, 2071, 2114,
2121, 2134, 2225, 2230, 2233, 2410, 2412, 2413, 2422, 2502, 2506, 2522, 2611,
2701, 2702, 3007, 3030, 3060, 3122, 3130, 3206, 3211, 3213, 3241, 3300, 3302,
3310, 3311, 3451, 3540, 3601, 3710, 4033, 4042, 4112, 4122, 4142, 4210, 4300,
4501, 5002, 5004, 5026, 5032, 5073, 5131, 5215, 5222, 5306, 5402, 6010, 6014,
6031, 6100, 6120, 6202, 6251, 7000, 7011, 7111, 7202, 7310, 7410, 7511, 8302,
9002, 9030, 9322, 10008, …
|
|
|
Facteurs
compté autant de fois que leur exposant |
32, 42, 60, 70, 104, 152, 231, 315,
316, 322, 330, 342, 361, 406, 430, 450, 540, 602, 610, 612, 632, 703, 722, 812,
1016, 1027, 1029, 1108, 1162, 1190, 1246, 1261, 1304, 1314, 1316, 1351, 1406,
1470, 1510, 1603, 2013, 2054, 2065, 2070, 2071, 2106, 2114, …
|
|
|
|
||
|
Nombres
dont la somme des chiffres divise trois fois la somme des chiffres des
facteurs. Facteurs
comptés une fois. |
402, 510, 1112, 1113, 1131, 1311,
2006, 2022,
2040, 2120, 2130, 2211, 3102, 3111, 3210, 4031, 5100, 7031, 8010, 10012,
10034, 10040, 10324, 11033, 11111, 11112, 11114, 11121, 11141, 11305, 12012,
12040, 12103, 12112, 12311, 12411, 12502, 13022, 13031, 13223, 13301, 14141,
15022, 16020, 16110, 20031, 20114, 20120, 20153, 20213, 20301, 20400, 21030,
21111, 21200, 21251, 21300, 22015, 22202, 23001, 23002, 23310, 24011, 24030,
24210, 30005, 30042, 30120, 30131, 30212, 30221, 30413, 31061, 31204, 31521,
32040, 32100, 32110, 32201, 32220, 32310, 33022, 36001, 40050, 40410, 42030,
43002, 44003, 45030, …
|
|
|
Facteurs
compté autant de fois que leur exposant |
402, 510, 700, 1113, 1131, 1311,
2006, 2022, 2130, 2211, 2240, 3102, 3111, 3204, 3210, 3220, 4031, 4300, 4410,
5310, 6004, 6100, 6300, 7031, 7120, 9000, 10034, 10125, 10206, 10251, 10304,
10413, 10521, 10612, 10800, 11033, 11111, 11114, 11116, 11121, 11141, … |
|
![]()
|
Voir |
|
|
Site |
|
|
Cette page |
![]()
