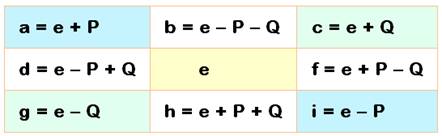|
||||||||||||||||||||||||||||||||||||
![]()
|
Carré magique 3 x 3 Propriétés Propriétés générales du carré
3x3 >>> Formules du carré magique 3 x3 >>> Propriétés des sommes de
produits >>> Résolution des équations du carré
magique 3x3 >>> |
Retour Carré
magique ordre 3
|
|
||||||||||
|
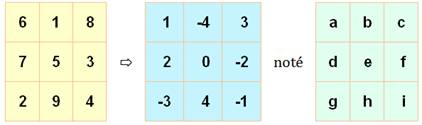
Soit le carré magique suivant
6x1x8 + 7x5x3 + 2x9x4 = 48 + 105 + 72 = 225 6x7x2 + 1x5x9 + 8x3x4 = 84 + 45 + 96 = 225
6x1 + 6x8 + 1x8 + 7x5 + 7x3 + 5x3 + 2x9 +
2x4 +9x4 = 195 6x7 + 6x2 + 7x2 + 1x5 + 1x9 + 5x9 + 8x3
+8x4 + 3x4 = 195
|
||||||||||
|
|
||||||||||
|
PRODUITS
par 3
* est le signe multiplier pour ne pas
confondre avec x; ^
est le signe puissance E1 = X*Y*Z+XX*YY*ZZ+XXX*YYY*ZZZ E2 =
X*XX*XXX+Y*YY*YYY+Z*ZZ*ZZZ
E1 = (a+b)*(a-b-c)*(a+c)+(a-b+c)*a*(a+b-c)+(a-c)*(a+b+c)*(a-b) = 3*a^3-3*a*c^2-3*b^2*a E2 = (a+b)*(a-b+c)*(a-c)+(a-b-c)*a*(a+b+c)+(a+c)*(a+b-c)*(a-b) = 3*a^3-3*a*c^2-3*b^2*a
PRODUITS
par 2
E3 = X*Y+X*Z+Y*Z + XX*YY+XX*ZZ+YY*ZZ + XXX*YYY+XXX*ZZZ+YYY*ZZZ E4 = X*XX+X*XXX+XX*XXX + Y*YY+Y*YYY+YY*YYY + Z*ZZ+Z*ZZZ+ZZ*ZZZ
E3 = (a+b)*(a-b-c)+(a+b)*(a+c)+(a-b-c)*(a+c)
+(a-b+c)*a+(a-b+c)*(a+b-c)+a*(a+b-c) +(a-c)*(a+b+c)+(a-c)*(a-b)+(a+b+c)*(a-b)
= -3*c^2-3*b^2+9*a^2 E4 = (a+b)*(a-b+c)+(a+b)*(a-c)+(a-b+c)*(a-c)
+(a-b-c)*a+(a-b-c)*(a+b+c)+a*(a+b+c)
+(a+c)*(a+b-c)+(a+c)*(a-b)+(a+b-c)*(a-b) = -3*c^2-3*b^2+9*a^2
Autres
caractéristiques
|
||||||||||
Section créée sur une idée de JEAN ARTIGUE
professeur retraité de l'Éducation Nationale – Merci
![]()
Résolution des équations des carrés magiques
|
Résoudre les équations des
carrés magiques |
|
|
|
Plusieurs
méthodes pour résoudre un carré magique. |
Cette méthode praticable pour n petit (3) est
rédhibitoire. Pour n = 4, il y a déjà 880 carrés magiques sur
20 922 789 888 000 permutations (242 jours de calcul à
raison d'un million de cas traités à la seconde. C'est Frénicle de
Bessy qui a trouvé ce nombre le premier en 1693. Ce compte exclut les carrés
obtenus par rotations et réflexions.
Méthode sans doute efficace mais réservée aux
mathématiciens d'un certain niveau.
1) Résolution classique des équations; ce qui
devient vite laborieux. 2) Utilisation de quelques astuces. Par exemple,
soustraire une constante pour obtenir une constante magique nulle. Il y a
encore plus fin! >>> 3) Utilisation de l'outil matrice et calcul
des valeurs propres (eigenvalues) pour accélérer la résolution du système
d'équations. |
|
|
|
||
|
Équations |
Avec les carrés d'ordre impairs, les sommes
peuvent être ramenées à 0 en soustrayant une constante à tous les nombres.
Celle-ci est égale à l'élément central soit: (n² + 1) / 2. |
|
|
Cas n = 3 |
|
|
|
Une
manière astucieuse pour résoudre le système d'équations: introduction des
valeurs P et Q qui symétrisent les résultats. |
|||
|
Somme des quatre équations impliquant e , l'élément central |
d+e+f+b+e+h+a+e+i+c+e+g
= 4m a+b+c+d+e+f+g+h
+ 3e = 4m 3m
+ 3e = 4m 3e
= m |
||
|
Égalité pour ces quatre cas |
d+e+f
= b+e+h = a+e+i = c+e+g = m = 3e d+f
= b+h = a+i = c+g = 2e |
||
|
En posant P et Q pour symétriser |
a + i = e + e a – e = e – i = P a = e + P |
c + g = e + e c – e = e – g = Q c = e + Q |
|
|
En tenant compte des sommes magiques sur les lignes et les
colonnes |
a + b + c = m = 3e e + P + b + e + Q = 3e b = e – P – Q a + d + g = 3e e + P + d + e – Q = 3e d = e – P + Q |
g + h + i = 3e e – Q + h + e – P = 3e h = e + P + Q c
+ f + i = 3e e
+ Q + f + e – P = 3e f
= e + P – Q |
|
|
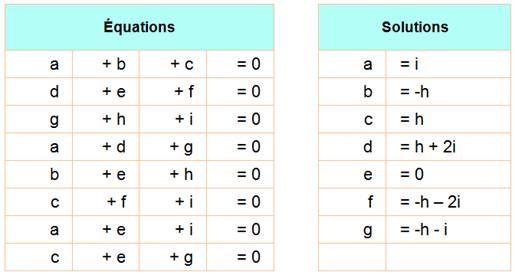
Soit le carré magique avec ses équations |
|
||
|
Existe-t-il
un carré magqiue d'ordre 3 dont les nombres sont des carrés? |
||
|
Reprise de équations trouvée en indiquant que les nombres
sont des carrés |
A² = e + P B² = e – P –
Q C² = e + Q E² = e |
F² = e + P – Q G² = e – Q H² = e + P + Q I² = e – P |
|
En sommant les éléments symétriques => 2 E² = quatre dois somme de
deux carrés |
A² + I² = B²
+ H² = C² + G² = F² + D² = 2e = 2E² |
|
|
Avec les produits => E4 est quatre fois somme de deux carrés |
A²I² = (E² + P)(E² – P) = E4 – P² B²H² = (E² – (P+Q)) (E² + (P+Q)) = E4 – (P+Q)² C²G² = (E² + Q)(E² – Q) = E4 – Q² F²D² = (E² + (P–Q)) (E² – (P–Q)) = E4 – (P–Q)² |
|
|
À ce
stade, les conditions d'obtention du carré magique carré sont sévères. Toujours
est-il que l'on ne connait aucun tel carré. |
||
|
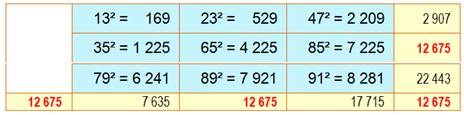
Un solution approchée: somme magique sur toutes les lignes
pasant par le centre. |
|
|
Voir Carrés
magiques avec carrés et cubes
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMord3Pt.htm |
![]()