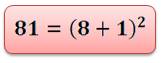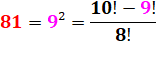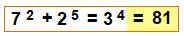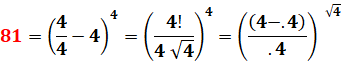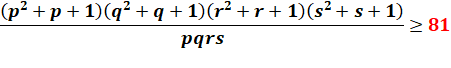|
|||||||||||||||||||||||||||||||||||
![]()
Énigme
|
Ma
Maman a 81 ans. Pour lui souhaiter son
anniversaire, je lui ai rédigé une jolie carte en lui présentant mes
meilleurs vœux pour ses 34 ans. Comment cela
se peut-il, sans mentir? Solution. |
|
Rétablir
l'égalité: 81
× 9 = 801 |
Voir
Jeux et énigmes / Pensées & humour
|
|
||||
|
TARN |
||||
|
81 = 34 = 92 |
THALLIUM
Tl |
|||
|
Propriétés Typiques |
81 = 9 x 9 = 90 – 9 81 = 9² & 9 = 1 + 8 |
FÊTE |
||
|
|
|
|||
|
|
||||||
|
|
Voir Numération 80 à 89 |
|||||
|
Taille
de la grille du Sudoku. |
||
|
que
l'indique la somme de ses chiffres. |
||
|
|
||
|
|
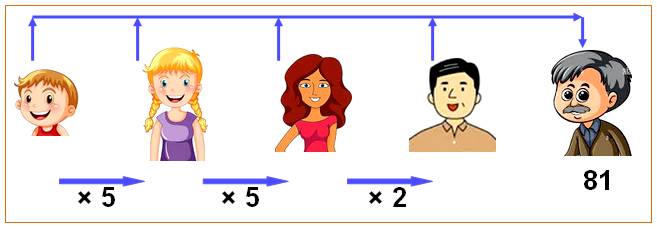
Retrouvez l'âge de chacun
|
|
||
|
Nombre
de Harshad presque narcissique Même
somme des chiffres (seul cas). Autre
forme:
|
Voir Nom des nombres
Voir Nombres
géométriques |
|
Chiffres et numération
|
81 + 18 = 99 |
||
|
81 / (8 + 1) = 9 81 / (8 + 1)² = 1 |
|
|
|
81 = 8+1 + 2+2+8+7+6+7+9+2+4+5+4+9+6+1 |
Somme
de ses chiffres et de ceux de sa puissance 7. |
|
|
8110 = 1873 8210 = 2837 |
Notez les
motifs avec les chiffres. |
|
|
81 = 9² et 8 + 1 = 9 324 = 18² et 2(3+2+4) = 18 1296 = 36² et 2(1+2+9+6) = 36 |
|
|
|
81 = 9 x (8 + 1) 18 = 2 x (1 + 8) |
|
|
|
& 8 + 1 = 9 1 458 = 18 x 81 & 1 + 4 + 5 + 8
= 18 |
|
|
|
81 =
3 . 33 18
= 2 . 32 |
||
|
81 = (8 + 1)²
|
Seul cas possible (hors cas triviaux: 0 et
1). Voir Motifs |
|
|
81
= 9 (8 + 1) |
|
|
|
81 =
90 – 9 |
|
|
Addition et soustraction
|
81 = 5 + 6 + … + 13 |
|
|
|
81 = T8 + T9
= 36 + 45 |
|
|
|
81 =
9² =
11+12+13+14+15+16 =
5+6+7+8+9+10+11+12+13 |
|
|
|
81 = 1 + 2 + 3 + 45 + 6 + 7 + 8 + 9 |
|
|
|
81
=
1 + 6 + 11 + 16 + 21 + 26 1, 9, 25, 49, 81 … 1, 1, 2,
4, 7, 13, 24, 44, 81 … |
|
|
|
81 = 34 = (1) |
Voir aussi
Nombre 34
|
|
|
81 +
82 + … + 90 = 91 + … + 99 |
|
|
|
81
/ (8 + 1) = 9 |
||
|
81
=
(18+2) + (18-2) + (18x2) + (18/2)
= (8+8) + (8-8) + (8x8) + (8/8) |
|
|
Multiplication, division, diviseurs
|
81 / (8 + 1) = 9 |
|
|
= 1 + 3 + 9 + 27 + 81 |
Liste: 1,
3, 22, 66, 70, 81, 94 …
Liste: 1,
81, 400, 32400, 1705636 … OEIS
A008848 |
|
79, [81, 104, 117, 156, 343, 375, 7 100] 81 = 34 et 82 = 2x41 => 82 – 3 = 79 |
|
|
|
|
|
81
= 35 / 31 = 34 = 93 / 91
= 92 |
|
![]()
|
81
= 9² = 1² + 4² + 8² = 3² + 6² + 6² = 4² + 4² + 7² 49
= 7² = 2² + 3² + 6² |
En rouge, termes différents
Le plus petit carré somme de trois carrés
différents est 49. |
|
||
|
81
= 9² et 8 + 1 = 9 = 3² 81
= 9² = 34 et 8 = 23 & = 13 |
|
|
||
|
|
|
|||
|
81 |
|
|||
|
81 =
3 x 33 |
|
|
81
= 34 = 9² = 25 + 72 = 32 + 49 |
|
|
81
= 9² = 1 + 3 + 5 + … + 17 |
|
|
|
|
|
81 = 9² = 1² + 4² + 8² = 3² + 6² + 6² = 4² + 4² + 7² = 2² + 2² + 3² + 8² = 2² + 4² + 5² + 6² = 2² + 3² + 4² + 4² + 6² = 1² + 1² + 1² + 2² + 5² + 7² = … = 3² + 3² + 3² + 3² +
3² + 6² |
etc.
= 9 x 3² = 3² x 3² = 9² |
|
|
|
|
81
= 41² – 40² = 41 + 40 = 9² |
|
|
81 = 41² – 40² = 9² =
9² x 1² |
|
|
81
= 1² + 4² + 8² = 2² + 4² + 5² + 6² |
|

|
= 13 + 23 + 23
+ 43 |
|
|
81
= 3 x 33 |
|
|
81
= 1 + 5 x 24 |
|
|
81
=
1 x 32 + 2 x 62 = 1 x 72
+ 2 x 42 = 1 x 32
+ 8 x 32 = 1 x 13
+ 10 x 23 = 9 x 13
+ 9 x 23 = 1 x 14
+ 5 x 24 = … |
|
|
81 = 1 + 16 + 64 |
|
|
= 1958459 8277756992 6302400511 = nombre premier |
|
|
81
= (10 – 1) (10 – 8) |
|
En puissance
|
812
= 6561 avec 65 = 61 + 4 |
|
|
|
819
= 150 094
635 296 999 121 & 1+5+0+…+2+1 = 81 |
|
|
|
8111
= 984770902183611232881 =>
9+8+4+…+1 = 90 9018
= 150094635296999121000000000000000000
=>1+5+0+…+0 = 81 |
|
|
![]()
|
|
Voir Nombre
de Lewis Carroll / Nombre 10125 |
Dénombrement - Jeux et curiosités
|
81 Quantité de régions dans un carré
partagé. |
|
|
|
|
Avec
.4 = 0, 4 = 2/5 |
|
|
81
= (10n+1 – 10 – 9n) / (1 + 11 + … + 11…1nfois) |
||
|
Propriété
Démonstration En divisant chaque terme par p, q, r
et s successivement
Pour chacun des facteurs, si p vaut
1 le facteur vaut 3 et si p est égal à 2 ou
plus, alors p+1 vaut 3 ou plus. Idem pour les autres. Conclusion: le produit est égal ou
supérieur à 3x3x3x3 = 81. |
![]()
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 1, 0, 0, 0, 1] 3, [1, 0, 0, 0, 0] 4,
[1, 1, 0, 1] 5,
[3, 1, 1] 6,
[2, 1, 3] 7,
[1, 4, 4] 8, [1, 2, 1] 9, [1, 0, 0] 10,
[8, 1] 11,
[7, 4] |
12,
[6, 9] 13,
[6, 3] 14,
[5, 11] 15,
[5, 6] 16,
[5, 1] 17,
[4, 13] 18,
[4, 9] 19,
[4, 5] 20,
[4, 1] 21,
[3, 18] |
22,
[3, 15] 23,
[3, 12] 24,
[3, 9] 25,
[3, 6] 26, [3, 3] 27,
[3, 0] 28,
[2, 25] 29,
[2, 23] 30,
[2, 21] 60,
[1, 21] |
26,
[3, 3] 80,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Sites |
|
|
Cette page |
![]()
|
Énigme maman En
fait, j'ai écrit 34. En décalant le quatre un peu vers le haut, il
devient exposant.
Il faut lire: 34 = 3 x 3 x 3 x 3 = 9 x 9 = 81. Énigme des âges à
retrouver x
+ 5x + 25x + 50x = 81 x = 81 Les
âges successifs sont donc: 1, 5, 25, 50 et 81 ans |
|
Rétablir l'égalité: 81
× 9 = 801 Retournez
l'expression: 108 = 6 × 18 |
![]()