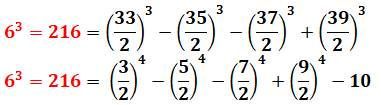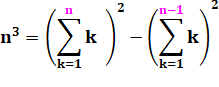|
Édition du: 27/04/2025 |
Faites
un double-clic pour un retour en haut de
page
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||||||||
Suite en propriétés
arithmétiques |
|
![]()
Chiffres et numération
|
216 + 612 = 828 |
|
|
|
21 + 6 = 27 = 33 |
|
|
|
216 = 23 x 33 |
|
|
|
216 = 198 + (1+9+8) =
207 + (2+0+7) |
|
|
|
216 divisible
par (2, 1 et 6) |
|
|
|
216 divisible par 9 et
12 |
|
|
|
216 =
61 + 2 |
|
|
|
21610
= 31204 |
|
|
|
216 +
612 = 828 |
|
|
|
216
/ (2 + 1 + 6) = 24 216
/ (2 x 1 x 6) = 18 |
|
|
Addition
et soustraction
|
216 = 22 + 11 + 111 +
6 + 66 |
|
|
216 =
6 + 7 + … + 21 |
|
|
216 =
31 + 33 + …+ 41 = 6 (1 + 3 + … + 11) |
Voir Brève
61-1213 |
|
216 =
108 + 72 + 36 |
|
|
216 =
107 + 109 |
|
|
216 =
6 + 7 + … + 21 216 =
20 + 21 + … + 28 216 =
71 + 72 + 73 |
Curiosité pour la première: départ
(6) et fin (21) de la somme forment le nombre (216). |
|
216 = 54 + 72
+ 90 = 63
et 543 + 723 + 903 = 1083 = 1 259 712 |
|
|
216 = T3 + T4
+ … + T10 |
|
Multiplication et division
|
216 = 23 .
33 & 2 × 3 = 3 + 3 |
|
|
216 =
3!3 = 63 |
|
|
216 =
4! x !4 = 24 x 9 |
Voir Jeu des nombres
faits avec des 4 |
|
216
= tau (554 400) |
|
|
Un monde de cubes avec les six plus petits
nombres
Expressions pour 216 = 63
Identité Identité
de Ramanujan
qui engendre les cubes, sommes de trois cubes:
Cas où: a = 1 et b = 0:
Nombre de Platon Ce nombre avec cette somme de cubes est. donné pour le nombre de Platon par certains,
d'autres affirmeront que c'est 12 960 000 = (3 x 4 x 5)4. |
Voir Pépites / Équations
diophantiennes / Triplet
isiaque
|
216 =
63 = 33 + 43 + 53 = 27 + 64 + 125 |
|
||
|
216 =
33 + 43 + 53 = 9 x 24 |
|
||
|
216 = 63 = 5 x 6
x 7 + 6 =
210 + 6 = 216 |
|
||
|
|
Voir Brève
61-1218 / |
||
|
216 =
63 = 23 x 33 = 63 = 6 x 6 x 6 = 6 x 36 = 3 x 6 x 12 |
|
||
|
216 =
63 = 15² – 3² = 21² – 15² = (15 + 6)² – 15² = 29² – 25² = 55² – 53² |
|
||
|
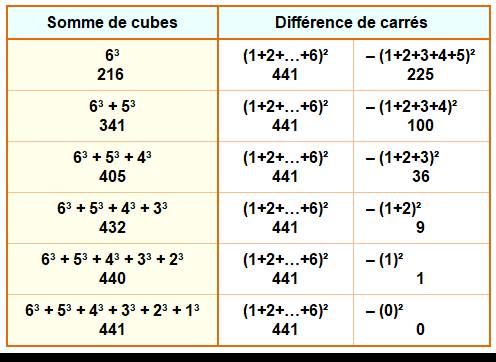
216 =
(1 + 2 + 3 + 4 + 5 + 6)² – (1 + 2 +
3 + 4 + 5)² = 21² – 15² = 63 |
|
||
Généralisation
de la propriété vue ci-dessus – Valable pour tous les cubes

Voir Brève 573
|
|
216 est un
nombre deux fois différence de carrés avec un terme commun (15) dans chaque
soustraction. |
|
216 =
4² + 6² + 8² + 10² 216 =
6² + 6² + 4·6² |
|
|
216 =
23 . 33 |
|
|
216 =
33 + 43 + 53
= (3x4) x 18 |
|
|
216 =
33 + 43 + 53 = 93 – 83 – 13 33 x 43 x 53 = 216 000 |
|
|
216 =
35 – 33 |
|
En puissance
|
216² =
46 656 258²
= 66 564 264²
= 69 696 408²
= 166 464 |
|
|
2162 =
46 656 et 4+6+6+5+6 = 27 = 33 |
|
Jeux
|
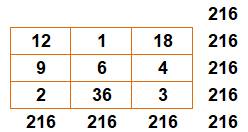
216
|
La constante est égale à (a × b)3
|
||
|
|
|
||
|
216 =
3!3 |
|
||
|
|
||
|
|
![]()
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 1,
0, 1, 1, 0, 0, 0] 3, [2, 2, 0, 0, 0] 4, [3, 1, 2, 0]
pannumérique 5, [1, 3, 3, 1] 6, [1, 0, 0, 0] 7, [4, 2,
6] 8, [3, 3,
0] 9, [2, 6,
0] 10, [2, 1,
6] 11, [1, 8,
7] |
12, [1, 6,
0] 13, [1, 3,
8] 14, [1, 1,
6] 15, [14,
6] 16, [13,
8] 17, [12, 12] 18, [12,
0] 19, [11,
7] 20, [10,
16] 21, [10,
6] |
22, [9,
18] 23, [9, 9] 24, [9, 0] 25, [8,
16] 26, [8, 8] 27, [8, 0] 28, [7,
20] 29, [7,
13] 30, [7, 6] 60, [3,
36] |
17, [12,
12] 23, [9, 9] 26, [8, 8] 35, [6, 6] 53, [4, 4] 71, [3, 3] 107, [2,
2] 215, [1,
1] |
Voir Bases
/ Brésiliens
![]()
|
Retour Suite |
|
|
Voir |
|
|
Voir |
![]()