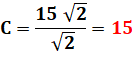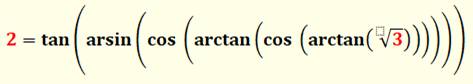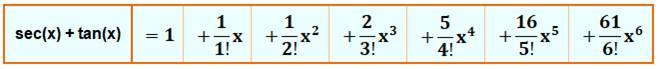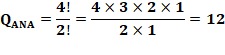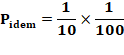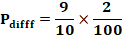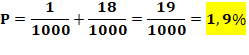NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 22

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

420. Prix Wolfskehl
Paul Wolfskehl, mathématicien né en 1856 à Darmstadt, promet une récompense à quiconque pourrait retrouver la preuve de Fermat (environ un million d'euros, mais devenu 30 000 euros pour Wiles du fait de l'inflation en Allemagne après la première guerre mondiale). Pourquoi cette générosité? La raison est controversée. Est-ce l’attachement de Wolfskehl à une mystérieuse jeune femme, jamais identifiée. La femme le repoussa. De désespoir, il décida de se suicider d'une balle dans la tête à minuit pile. En attendant, il se rendit dans sa bibliothèque et commença à feuilleter des documents de mathématiques.		Il tombe sur le travail d'Ernst Kummer (1810-1893), qui avait démontré qu'il y avait une erreur dans la preuve du dernier théorème d'Augustin Cauchy (1789-1857). Piqué au vif, il tente de prouver que Kummer avait tort et que la preuve de Cauchy nécessitait simplement une légère mise au point. Il travaille jusqu'à l'aube pour constater que Kummer avait bel et bien raison. La conjecture de Fermat résiste. Le délai de minuit est passé! Wolfskehl est tellement enthousiasmé par les mathématiques qu'il abandonne l'idée du suicide et décide de créer le fameux prix.
*Une autre source* explique que Wolfskehl, forcé de rester en chaise roulante, ne pourra pas être docteur. Alors, il s'est tourné vers les mathématiques. Le prix aurait été créé en hommage à cette nouvelle vie.		*Une autre source* dit qu'on l'aurait obligé à épouser une garce et que le prix ainsi mis en jeu échappait à sa succession.
Brèves associées	>>> Théorème de Fermat-Wiles		>>> Les 23 problèmes de Hilbert
Pour en savoir plus	>>> Théorème de Fermat-Wiles – Historique

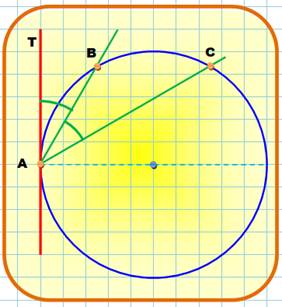
421. Tangente sans le centre
Construction Arc de cercle (bleu; ici cercle complet). *Le centre est non connu* Point A quelconque. Point B et C tel que arc AB = arc BC. Angle BÂT tel que BÂT = BÂC. AT est la tangente en A au cercle. Cette construction est souvent intéressante même si le centre est connu. Explications Les angles BÂT et BÂC sont égaux (construction). Ils interceptent des arcs égaux. Pour BÂC, c'est l'arc BC. Pour BÂT, c'est forcément AB (= BC). L'angle qui intercepte l'arc AB est formé du segment AB et l'autre côté est nécessairement la tangente en A.
Brèves associées	>>> Construction de la médiatrice	>>> Cercle de Ford
Pour en savoir plus	>>> Construction de la tangente	>>> Tracé du cercle sans le centre

422. Logarithme et âge du chien
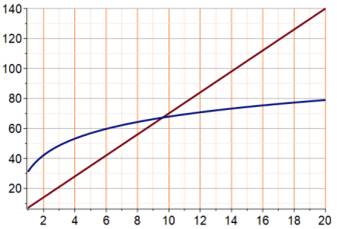
Une étude récente (2019) a montré que le facteur sept pour calculer un âge équivalent du chien est un mythe. On aurait C = 15 ans pour le chien qui serait équivalent H = 7 x 15 = 150 ans des hommes. L’Université de Californie à San Diego (États-Unis), après étude de l’influence de l’ADN sur l’âge des Labradors (épigénétique), propose une formule comprenant un logarithme : H = 16 ln C + 31		Graphe : âge équivalent humain du chien On donnait 2 x 7 = 14 ans à un chien de 2 ans ; il faudrait plutôt lui attribuer 42 ans.
Brèves associées	>>> Logarithme – Un aperçu		>>> Épigénétique
Pour en savoir plus	>>> Logarithme – Introduction, développements		>>> Âge de Diophante

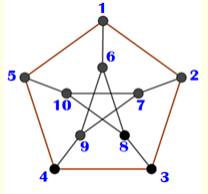
423. Colorier le graphe pentagonal
Énigme Le défi consiste à colorier chacun des dix sommets de ce graphe de sorte que deux sommets réunis par un segment soit de couleur différente. Défi Trouver d'autres solutions.
Brèves associées	>>> Hexagone magique	>>> Le fortin et ses gardes
Pour en savoir plus	>>> Colorier le graphe – Méthode	>>> Le problème des quatre couleurs

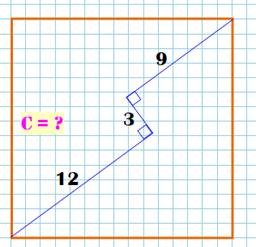
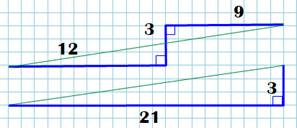
424. Diagonale brisée
Énigme On connait les dimensions de cette diagonale brisée à angles droits. Trouver la longueur du côté du carré. Solution Tracer la diagonale (verte) et translater deux segments de sorte que l'on retrouve un triangle rectangle. Avec Pythagore: D² = 21² + 3² = 450 D = 15 Encore Pythagore pour le côté: C² + C² = D² = 2 C²		Carré avec diagonale brisée Détail pour solution
Brèves associées	>>> Carré et deux triangles équilatéraux		>>> Périmètre du rectangle divisé
Pour en savoir plus	>>> Carré est ses propriétés		>>> Géométrie – Index

425. Formule pour passer de 3 à 2
Formule trigonométrique qui transforme les nombres entiers. Tout nombre n est égal à cette fonction en y injectant n² – 1 à la place du 3.		2 = F(3 ) = F(2² – 1) 10 = F(10² – 1) = F(99) n = F(n² – 1)
Brèves associées	>>> Lignes trigonométriques		>>> Valeurs trigonométriques principales
Pour en savoir plus	>>> Nombres entiers trigonométriques		>>> Trigonométrie en première

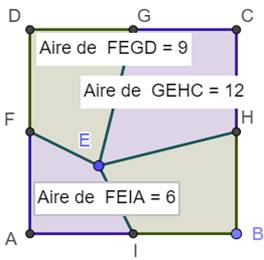
426. Aire dans le carré divisé
Énigme ABCD est un carré. Les points F, G, H et I sont les milieux des côtés. Le point E est quelconque. Quelle est l'aire du quatrième quadrilatère ? Solution On montre assez facilement la propriété suivante sur une telle figure: Aire verte = aire violette 1 2 + 6 = 9 + x x = 9
Brèves associées	>>> Rectangle divisé – Périmètre	>>> Carrés et dominos en périphérie
Pour en savoir plus	>>> Explication de cette énigme	>>> Carré – Index

427. Nombre premier et Constante e
Le quatre plus petits nombres premiers formés à partir des chiffres de e = exp(1) 2, 271, 2 718 281, 27182 8182845904 5235360287 4713526624 9775724709 3699959574 9669676277 2407663035 3547594571 = 0,27183 10⁸⁵ (84 chiffres) DicoNombre: nombre 2, 271, 2 718 281		Facteurs pour les dix premiers nombres formés avec e 2, 2, 2 7, 27, 3³ 1, 271, 271 8, 2718, 2 x 3² x 151 2, 27182, 2 x 13591 8, 271828, 2² x 67957 1, 2718281, 2718281 8, 27182818, 2 x 13 x 1045493 2, 271828182, 2 x 3 x 45304697 8, 2718281828, 2² x 97 x 179 x 39139
Brèves associées	>>> Constante e = 2,7 1828 1828		>>> Premiers en 6k+1 et 6k+5
Pour en savoir plus	>>> Constante e et nombres premiers		>>> Fonction exponentielle

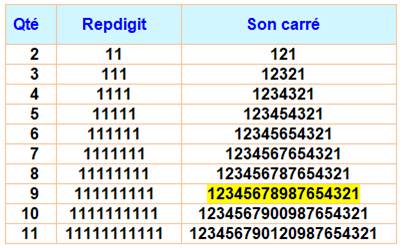
428. Repunits et palindromes
Les carrés des repunits de 2 à 9 sont palindromes et forment un nombre en vague avec les nombres successifs à partir de 1. Celui en jaune est pannumérique: il utilise tous les chiffres de 1 à 9. On note ce produit de carrés: 11111² = 41² x 271² = 123454321		Un repunit est aussi un repdigit particulier
Brèves associées	>>> Palindromes		>>> Pépites numériques
Pour en savoir plus	>>> Repunits et palindromes		>>> Pannumériques

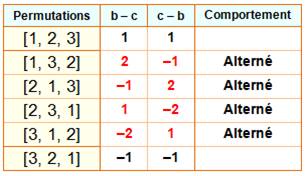
429. Permutations alternées
Le mathématicien français Désiré André en 1879 travaille sur les permutions des nombres. Il ne retient que celles en rouge sur ce tableau. Faisant la différence entre les chiffres successifs, il ne garde que les cas où le signe alterne.		Exemple de permutation alternée pour [1 à 8] Quantité Pour les permutations qui commencent par un signe positif, la quantité de permutations est: [3, 2], [4, 5], [5, 16], [6, 61], [7, 272], … Ex: avec 7 chiffres, il y en a 272. Désiré André a trouvé la formule qui permet de calculer ces nombres. Ce sont les numérateurs de la relation indiquée ci-dessous. Il s'agit d'un développement en série d'une fonction trigonométrique simple: sécante (x) + tangente (x). Un relation magique pour un mathématicien !

Brèves associées	>>> Factorielle		>>> Triangle de Pascal
Pour en savoir plus	>>> Permutations alternées d'Euler >>> Permutations		>>> Nombres à motifs – Index >>> Polynômes générateurs

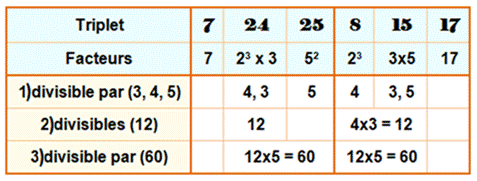
430. Divisibilité des triplets de Pythagore
Il existe une infinité de triplets de Pythagore; (3, 4, 5) est le plus petit. Nombreuses propriétés de divisibilité: deux sont impairs et un est pair; divisibilité par 3, 4 et 5; et divisibilité du produit par 60. Le triplet (3, 4, 5) est représentatif.		Deux exemples
Brèves associées	>>> Triplets de Pythagore: a² + b² = c²		>>> Triplets doublement carré
Pour en savoir plus	>>> Propriétés des triplets de Pythagore		>>> Triplet (3, 4, 5) et triangle

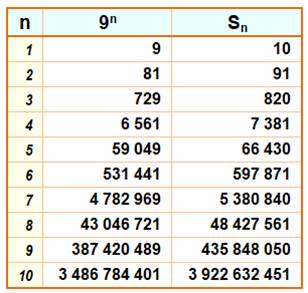
431. Somme des puissances de 9

Énigme

9⁰ + 9¹ + 9² + … + 9²⁰²⁰ = …u ? (chiffre des unités)

Unités des puissances et de leur somme

Les puissances de 9 se terminent alternativement par 1 et 9.

Leur somme (1 + 9^1 + 9^2 + …+ 9^n) se termine alternativement par 1 et 0.

L'unité vaut 1 pour n pair.

Réponse à l'énigme: n = 2020 (pair) => u = 1

Valeur de la somme

Explication du calcul: voir Somme des puissances de 9

La somme est un nombre triangulaire, soit la somme des entiers jusqu'à m, avec la valeur de m:

Exemple

S₅ => m = (3⁵⁺¹ – 1) / 2 = 364

Somme des entiers de 1 à 364:

364 x 365 / 2 = 66 430

Vérification

Une puissance de 9 se termine par 9 ou 1.

La somme des puissances se termine par 0 ou 1.

Brèves associées

>>> Somme des carrés des entiers

>>> Somme de chiffres et divisibilité par 9

Pour en savoir plus

>>> Somme des puissances de 9

>>> Nombres triangulaires

>>> Somme des entiers

>>> Puissances de 3 et de 9

432. 2-Repdigits au cube
Tous les 2-repdigits (nombres avec "2" uniquement) au cube jusqu'au sixième ne contiennent pas de "2". Record des cas où un k-repdigit ne contient pas le chiffre k.		Rang, Nombre, Son cube, Chiffres non utilisés 2, 22, 10648, {2, 3, 5, 7, 9} 3, 222, 10941048, {2, 3, 5, 6, 7} 4, 2222, 10970645048, {2, 3} 5, 22222, 10973607685048, {2} 6, 222222, 10973903978085048, {2, 6} 7, 2222222, 10973933607682085048, {}
Brèves associées	>>> Repunits et palindromes >>> 3- Repdigits au cube		>>> Nombres uniformes – Repunits
Pour en savoir plus	>>> k-repdigit et le chiffre k		>>> Repdigits

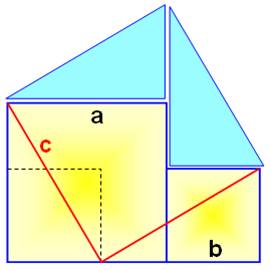
433. Théorème de Pythagore
L'aire du grand carré oblique est égale l'aire des deux carrés jaunes. Construire les deux carrés jaunes de côtés a et b. En reportant le petit carré dans le moyen (pointillés), on trace la ligne rouge qui engendre deux triangles rectangles identiques de côtés a, b et c. Ces deux triangles déplacés en position bleue forment le grand carré oblique de côté c. En exprimant les aires: c² = a² + b²
Brèves associées	>>> Triangle et les nombres 3, 4, 5, 6	>>> Triplets de Pythagore: a² + b² = c²
Pour en savoir plus	>>> Théorème de Pythagore	>>> Triangle rectangle

434. Retournés proportionnels

Nombres dont un multiple est son retourné (les mêmes chiffres lus à l'envers).

Tous les cas de 2 à 9 chiffres.

4	×	2 178	=	8 712
9		1 089		9 801
4		21 978		87 912
9		10 989		98 901
4		219 978		879 912
9		109 989		989 901
4		2 199 978		8 799 912
9		1 099 989		9 899 901

4	×	21 999 978	=	87 999 912
9		10 999 989		98 999 901
4		21 782 178		87 128 712
9		10 891 089		98 019 801
4		219 999 978		879 999 912
9		109 999 989		989 999 901
4		217 802 178		871 208 712
9		108 901 089		980 109 801

Brèves associées

>>> Nombres pannumériques

>>> Pépites numériques

Pour en savoir plus

>>> Retournés proportionnels

>>> Nombres retournés

435. Anagrammes des nombres
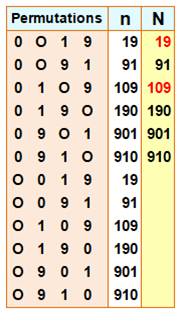
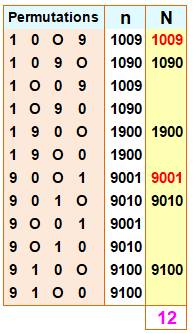
Comment compter les anagrammes en cas de présence de chiffres répétés ? Même si les "0" sont omis dans l'écriture des nombres, ils sont présents implicitement et la méthode générale s'applique. Avec le nombre 1009, il a quatre chiffres dont deux répétés: En rouge les quatre nombres premiers: 19, 109, 1009, 9001. Le nombre 1009 est multi-premier.		Exemple de dénombrement des anagrammes de 1009 Notez que les deux "0 " sont différenciés pour le recensement.
Brèves associées	>>> Factorielle		>>> Arrangements – Tiercé
Pour en savoir plus	>>> Nombres multi-premiers		>>> Anagrammes de Mississippi

436. Anagrammes entre deux nombres

Quelle est la probabilité que deux nombres à deux chiffres (de 0 à 99) soient anagrammes ?

Décompte par logiciel

0 à 9	10	sur	100
10 à 99	162		8 100
0 à 99	190		10 000

Soit une probabilité de 190 /10000 = 1,9%

Pourquoi pas la somme ?

On observe: 190 et 10 + 162 = 172.
Une différence de 18. Pourquoi ?

Parce que l'on compte les cas comme 20 et 02 et inversement, soit 2 x 9 = 18 cas en plus.

Avec deux chiffres (de 1 à 9)

Il y a 161 sur 7 921 possibilités: 2,33%

Avec trois chiffres (de 0 à 999)

Il y a 5 140 sur 10⁶ possibilités: 0,514%

Avec quatre chiffres (de 0 à 9999)

Il y a 175 870 sur 10⁸ possibilités: 0,175%

Calcul de probabilité pour deux chiffres

Il y a 100 nombres à deux chiffres y compris ceux en 00, 01, 02 …

Il y a 10 possibilités que les nombres soient avec chiffres identiques.

Probabilité:

On peut dire aussi qu'il y a 100 cas favorables pour 10 000 tirages, soit 1 / 1000.

Il reste 9 possibilités sur 10 que les nombres soient à deux chiffres différents, chacun existant deux fois:

Les cas sont exclusifs, les probabilités s'additionnent:

Brèves associées

>>> Anniversaire le même jour

>>> Combinaisons de 7 parmi 15

Pour en savoir plus

>>> Calcul de probabilités

>>> Anagramme numériques

437. Cubes et 1, 2, 3, 4, 5, 6
Association de ces six premiers nombres pour former des opérations avec les cubes. On connait le célèbre triplet de Pythagore dit, triplet isiaque: 3² + 4² = 5². Avec le même triplet de nombres au cube, on obtient le nombre suivant (6) au cube. Remarquable!		En prime, le nombre de Platon: (3 x 4 x 5)⁴ = 60⁴ = 6³ x 60 000
Brèves associées	>>> Triplets de Pythagore 3² + 4² = 5²		>>> Nombre 3
Pour en savoir plus	>>> Nombre 216 = 6³ >>> Nombre de Platon		>>> Triplet Isiaque

438. Divisibilité par 8
Critères Le critère classique de divisibilité par 8 dit qu'un nombre est divisible par 8, si ses trois derniers chiffres le sont. Il existe plus simple ! Les trois derniers chiffres du nombre sont notés cdu (centaines, dizaines et unités). Prendre cd et ajouter u/2. Si cette somme est divisible par 4, le nombre initial est divisible par 8 Exemples avec la moitié des unités (u/2) 123 416 => 41 + 3 = 44 = 11 x 4 => divisible par 8 456 984 => 98 + 2 = 100 = 25 x 4 => divisible par 8		Explications cdu = 100c + 10d + u = 8k On retire un maximum de multiples de 8: = (80c + 20c) + (8d + 2d) = 80c + 8d + 20c + 2d + u = 8(10c + d) + 2(10c + d) + u = 8k Le premier terme étant divisible par 8, le second doit l'être lui-aussi: 2(10c + d) + u = 8k 10c + d + u/2 = 4h
Brèves associées	>>> Divisibilité par 11	>>> Divisibilité de 123456789 – Critères
Pour en savoir plus	>>> Divisibilité par 8	>>> Crières de divisibilité

439. Somme 30
Énigme Choisir trois balles parmi les huit proposées pour satisfaire cette égalité. La somme de ces trois nombres doit être égale à 30. *Vous réaliserez rapidement que c'est infaisable, mais il y a un truc !* Voir Solution
Brèves associées	>>> Pesée des neuf billes	>>> Brèves et énigmes – Index
Pour en savoir plus	>>> Toutes les solutions de cette énigme	>>> Le bonhomme et les chaussures

Retour	Brèves de maths – Page 21
Suite	Brèves de maths – Page 23
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve22.htm

Solution

Solution proposée par une petit astucieux qui retourne la boule 9 pour en faite un 6.

Retour / Autres solutions

420. Prix Wolfskehl

421. Tangente sans le centre

422. Logarithme et âge du chien

423. Colorier le graphe pentagonal

424. Diagonale brisée

425. Formule pour passer de 3 à 2

426. Aire dans le carré divisé

427. Nombre premier et Constante e

428. Repunits et palindromes

429. Permutations alternées

430. Divisibilité des triplets de Pythagore

431. Somme des puissances de 9

432. 2-Repdigits au cube

433. Théorème de Pythagore

434. Retournés proportionnels

435. Anagrammes des nombres

436. Anagrammes entre deux nombres

437. Cubes et 1, 2, 3, 4, 5, 6

438. Divisibilité par 8

439. Somme 30