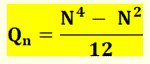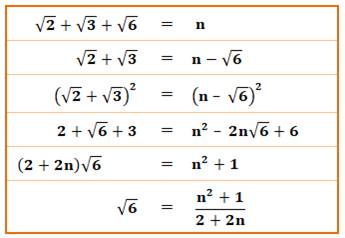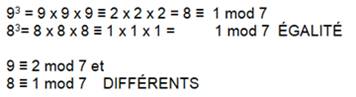|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 48 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
940. Table d'additions "magique" |
|
|||
|
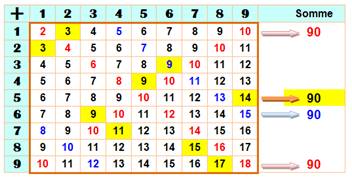
Additions dans le
table d'additions Soit la table d'addition des nombres de 1 à 9. Sur chaque
ligne, prenez un nombre dans une colonne différente et ajoutez-les. Propriété La somme de ces neufs nombres est toujours 90. Explication Aucun mystère ! Chaque nombre du tableau est l'addition de deux
nombres:
Chaque somme partielle (1 + 2 + … + 9 = 45)
contribue à la somme totale: 2 × 45 = 90. |
Table d'addition
Exemples de sommes À droite, on montre quatre exemples:
|
|||
|
Brèves associées |
>>>
Addition de nombres entiers |
>>>
Brèves Calcul – Index |
||
|
Pour en savoir plus |
>>>
Sommes avec les additions >>>
Carrés latins |
>>>
Calcul – Index |
||
941. Aire du triangle avec le cercle inscrit |
|
|||
|
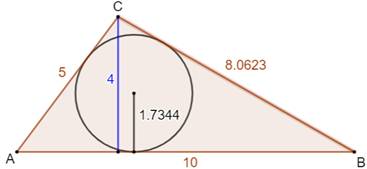
Formule pour tout triangle A = ½ r · P r rayon
du cercle inscrit et P périmètre Exemple Demi-périmètre = ½ (10 + 5 + 8,0623)
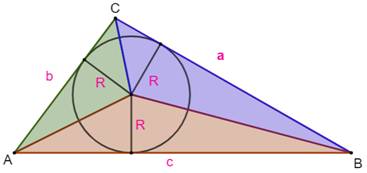
= 11,53115 Aire du triangle = 11,53115 × 1,7344 = 19,999 Calcul classique: ½ 10 × 4 = 20 Démonstration (figure du bas) L'aire du triangle est égale à la somme des aires des trois triangles
colorés. Leur hauteur est le rayon du cercle inscrit. Les bases sont les côtés a, b et c. Avec l'aire = base × hauteur, on a: A = ½ ar + ½ br + ½ cr = ½ r (a + b + c) |
|
|||
|
Brèves associées |
>>>
Triangle
rectangle inscrit et points |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Aire du triangle quleconque |
>>>
Triangle – Index |
||
942. Carrés dans grille carrée |
|
|||
|
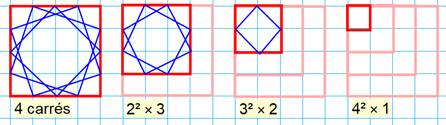
Types de carrés
Dénombrement Les carrés droits prennent toutes les tailles de 1 à n et il en existe
autant que de possibilités de déplacements du carré dans la grille. Il y a autant de carrés obliques inscrits dans une grille rouge que de
cases par côté, en comptant le rouge. Formule La quantité totale Qn
de carrés dans une grille de N points par côté est:
|
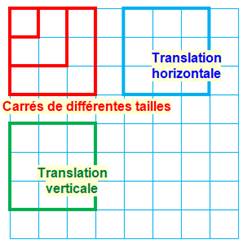
Principe du dénombrement
Principe du déplacement (ou translation)
Exemple pour une grille de 4×4, soit N = 5 points par côté Qn
= (54 – 52) / 12 = (625 – 25) / 12 = 600 / 12 =
50 |
|||
|
Brèves associées |
>>>
Rectangles
dans un quadrillage |
>>>
Brèves Dénombrement – Index |
||
|
Pour en savoir plus |
>>>
Calcul détaillé des carrés dans une grille |
>>>
Jeux de grile – Index |
||
943. Énigme virale sur le Net |
|
||
|
"Si vous réussissez à résoudre cette énigme
vous êtes un génie ! " Ces appels sont destinés à augmenter le nombre de
vues sur les pages de l'annonceur. Les énigmes de ce type sont nombreuses sur
Internet. Une sorte de marketing du site. Énigme typique avec ses pièges ! –
Solution en un seul tableau
Source: Si
vous réussissez cette énigme mathématique en moins de 30 secondes, vous
... - 59 Hardware |
|||
|
Brèves associées |
>>>
Énigme virale |
>>>
Brèves Énigmes – Index |
|
|
Pour en savoir plus |
>>>
Énigme virale – 2020 et suite |
>>> Équations du premier degré |
|
944. Nombres palindromes-facteurs |
|
|||
|
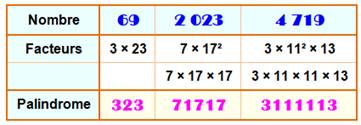
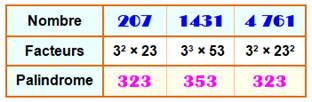
Définition PF Un nombre palindrome-facteurs (PF)
est un nombre dont les chiffres de TOUS les facteurs concaténés forment un
palindrome. Exemple
|
Définition PJF Un nombre palindrome-jeu de facteurs
(PJF) est un nombre dont les chiffres du jeu de facteurs (sans les exposants)
concaténés forment un palindrome. Exemple
|
|||
|
Brèves associées |
>>>
Palindromes
|
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Palindrome-Facteur |
>>>
Palindrome |
||
945. Suite des "1" désignés |
|
|||
|
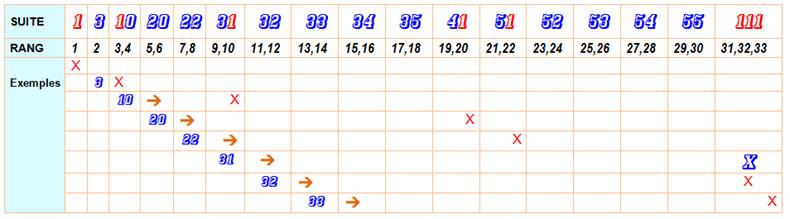
Définition Cette suite de nombres indique la position des
chiffres "1" dans cette même suite. Suite 1, 3, 10, 20,
22, 31, 32, 33, 34, 35, 41, 51, 52, 53, 54, 55, 111, 112, 200, 210, 220, 222,
… |
Exemple Le nombre 20 indique qu'il existe un chiffre"1"
en vingtième position, comme le montre le
tableau ci-dessous. |
|||
|
|
||||
|
Brèves associées |
>>>
Suite de
Sherlock Holmes |
>>>
Brèves Suites – Index |
||
|
Pour en savoir plus |
>>>
Suite des "1" |
>>>
Suites |
||
946. Somme de nombres |
|
||||
|
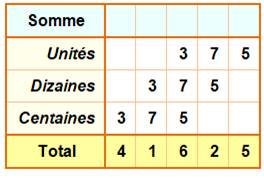
Question Nombres à trois chiffres formés avec les seuls
chiffres 1, 2, 3, 4 et 5 qui peuvent être répétés. Combien ? Quelle est leur somme ? |
Réponse Il y a 125 tels nombres Somme 41 625 |
||||
|
Somme (S) Le chiffre des unités de S est égal à 25 fois
chaque chiffre. Leur somme est égale à: Idem pour le deuxième comme pour le troisième. |
|
||||
|
Brèves associées |
>>>
Somme
paradoxale de Ramanujan |
>>>
Brèves Opérations – Index |
|||
|
Pour en savoir plus |
>>>
Somme de nombres (explications) |
>>> Jeux
avec les chiffres |
|||
947. Somme irrationnelle |
|
|||
|
Sommes d'irrationnels Nous savons que En revanche,
Somme de racine de 2, racine de
3 et racine d 6.
La démonstration (à droite) montre que cette
somme est effectivement irrationnelle. Notez que l'on a profité du fait que: |
Démonstration par contradiction: on suppose n rationnel.
D'un côté de l'égalité, on a un irrationnel et de l'autre un
rationnel. Contradiction ! La somme n est irrationnelle. |
|||
|
Brèves associées |
>>>
Sommes
des premiers – Goldbach |
>>>
Brèves Théorie – Index |
||
|
Pour en savoir plus |
>>>
Somme de nombres irrationnels |
>>>
Racine de 2 est irrationnelle |
||
948. Babbage et Ada Lovelace |
|
|||
|
Charles Babbage (1791-1871) Polymathe,
mathématicien et inventeur visionnaire britannique. Sa machine analytique ou machine
à calculer est créée en 1834. Elle fait suite à sa machine à différences qui établit les
tables de calculs sans erreur. Cette nouvelle machine sera programmable au
moyen de cartes perforées. Son fils construira une machine qui fonctionne et
qui est toujours exposée au Sciences Museum de Londres. Ada Lovelace (1815-1852) Elle apporte son aide pour programmer la machine
de Babbage. Pionnière de la programmation ! Non seulement elle a écrit les premiers
programmes mais elle a entrevu et décrit certaines possibilités offertes par
les calculateurs universels, bien au-delà de ce qu'imaginaient Babbage et ses
contemporains. |
Première machine analytique (1840)
|
|||
|
Brèves associées |
>>>
Tissus –
Géométrie des tissus |
>>>
Brèves Sciences – Index |
||
|
Pour en savoir plus |
>>>
Charles Babagge >>>
Ada Lovelace |
>>>
Ordinateurs – Historique |
||
949. Microprocesseurs – Gravure |
|
||
|
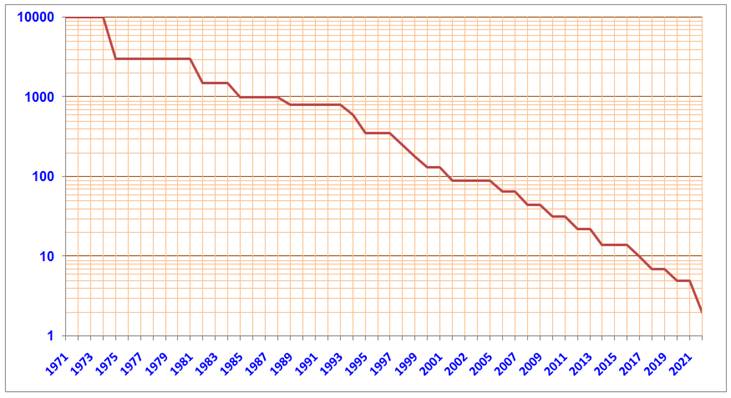
Évolution de la l'épaisseur en nanomètres de la gravure des microprocesseurs Facteur 5 000 en 50 ans (de 10 µm à 2 nm)
Anecdote personnelle: en 1971, en
tant que chef de projet et avec toute une équipe, nous avions conçu et
réalisé un ordinateur 24 bits qui tenait dans le volume d'un four à
micro-onde d'aujourd'hui. Quand, en fin de cette année là, un représentant
de la société Intel m'apprend que tout cela va tenir dans une simple puce ! C'était le microprocesseur 4 bits nommé 4004 (Illustration). |
|||
|
Brèves associées |
>>>
Nanotechnologies |
>>>
Brèves Sciences – Index |
|
|
Pour en savoir plus |
>>>
Microprocesseur – Gravure |
>>> Loi
de Moore |
|
950. Partage du carré en trois |
|
|||
|
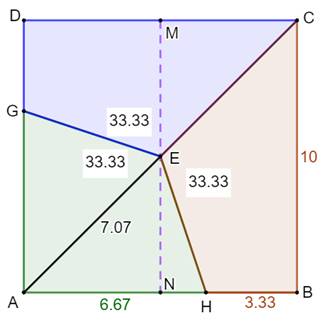
Partage du carré en trois Soit un carré de 10 cm de côté. Comment le
partager en trois parties de même aire ? Construction Diagonale AC du carré. Médiatrice MN Tiers sur les côtés: DG et BH. Les quadrilatères colorés ont la même aire. |
|
|||
|
Brèves associées |
>>>
Carré
penché sur trois carrés |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Partage du carré (calcul des aires) |
>>>
Doubler le carré |
||
951. Rectangle en carré |
|
|||
|
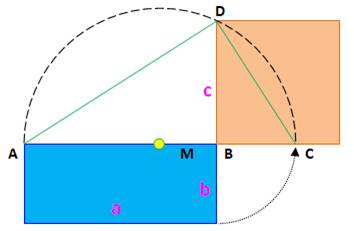
But Comment effectuer la quadrature du rectangle ? Construction à la règle et au compas d'un carré
de même aire que le rectangle. Construction: Un rectangle (bleu). Les deux côtés de même sommet B sont prolongés. Report de la largeur b sur l'autre côté pour
former le segment BC. Milieu M du segment AC. Cercle de centre M et de rayon MA. Intersection avec un prolongement du côté en D. BD est l'un des côtés du carré de côté c, de même
aire que le rectangle. Ce procédé est utilisé pour réaliser la
quadrature du polygone quelconque. |
Carré et rectangle de même aire
Justification La hauteur (BD = c) du triangle rectangle est
liée aux segments découpés sur l'hypoténuse par:
|
|||
|
Brèves associées |
>>>
Quadrature
du cercle |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Quadrature
du polygone |
>>>
Hauteur
d'un triangle rectangle |
||
952. Retrouver les activités |
|
|||
|
Énigme Abel, Babette, Cricri et Dany ont des passions.
Ils peuvent cuisiner, faire du kayak, de l’escalade et de la tyrolienne. Chaque enfant a une activité préférée différente. 1.
L’activité préférée d'Abel n’est pas l’escalade. 2.
Babette a peur des hauteurs. 3.
Cricri ne peut pas faire son activité préférée sans porter un harnais. 4.
Dany aime avoir les deux pieds sur terre en tout temps. Retrouvez l'activité de chacun. |
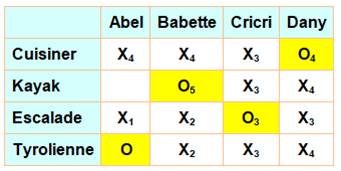
Solution Un tableau simple aide à résoudre l'énigme.
|
|||
|
Brèves associées |
>>>
Le soldat
épargné – Pb de Josèphe |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Énigme
semblables – Intégrammes |
>>> Logique – Index |
||
953. Vitesse de la lumière |
|
|||
|
Pourquoi la
vitesse de lumière est constante ?
D'après Heino Falcke |
||||
|
Brèves associées |
>>>
Relativité:
sa formule |
>>>
Brèves Sciences – Index |
||
|
Pour en savoir plus |
>>> Vitesse de la
lumière |
>>> Sciences – Index |
||
954. T-shirt troué |
|
|||
|
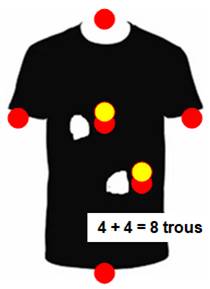
Énigme Combien de trous dans ce T-shirt ? Attention ce n'est pas deux !
|
Solution
Oui, on voit à travers les trous. Chaque tache
blanche représente deux trous. Oups! Si le dos est ajouré, il reste 7 trous ! |
|||
|
Brèves associées |
>>>
Séquence
miroir |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Énigme
classiques 2022 |
>>>
Tests te
défis – Index |
||
955. Carré magique et retourné |
|
|||
|
Prenez ce carré magique 3x3. Formez un nombre avec trois de ces chiffres. Formez les deux autres possibles.
La somme des carrés de ces nombres
et égale à la somme des carrés des mêmes nombres, mais retournés. Exemple: 492 est le
retourné de 294 |
Six configurations parmi douze
ayant la propriété d'égalité des sommes des carrés
|
|||
|
Brèves associées |
>>>
Carré
magique 3x3 – Permutations |
>>>
Brèves Carrés maiques – Index |
||
|
Pour en savoir plus |
>>>
Carré
magique et retourné (détails) |
>>>
Carrés
magiques – Index |
||
956. Sommes partielles d'entiers |
|
||
|
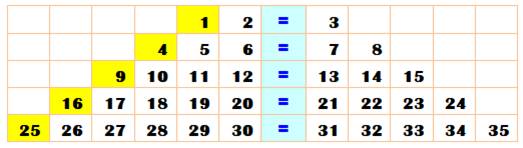
Propriété étonnante: égalité sans fin de sommes
d'entiers consécutifs
Notez que le nombre
en-tête (en jaune) est un carré; on trouve les carrés successifs. Pas si mystérieux !
L'indice
derrière le crochet indique la quantité de termes. Formule
pour la somme: k3 + k² + k(k + 1) / 2;
Pour k = 5: 125 + 25 + 5 × 3 = 165 En bleu
dans le formule, la somme
des entiers de 1 à k. Théorème La somme de k + 1 nombres successifs à partir de k² est égale à la somme des k suivants.
|
|||
|
Brèves associées |
>>>
Sommes
particulières avec 200 |
>>>
Brèves Opérations – Index |
|
|
Pour en savoir plus |
>>>
Égalité
de sommes d'entiers |
>>>
Énigme
des cinq pots |
|
957. Calcul des puissances – Un truc |
|
||
|
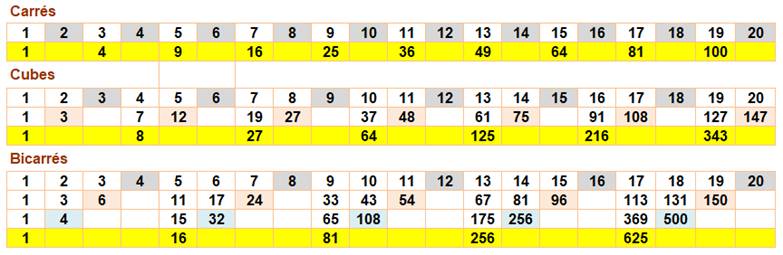
Pour trouver la suite des carrés:
Pour trouver la suite des cubes:
|
|||
|
Brèves associées |
>>>
Puissances
en folie |
>>>
Brèves Opérations – Index |
|
|
Pour en savoir plus |
>>>
Calcul
des puissances – Un truc |
>>>
Calculs – Index |
|
958. Triangle invariant |
|
|||
|
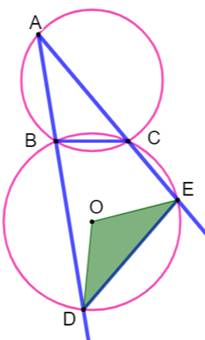
Construction Deux cercles sécants. Des sécantes issues d'un point A quelconque situé
sur un des cercles. Elles passent par les points d'intersection des
cercles. Elles engendrent les point d'intersection D et E Propriété Quelle que soit la position du point A sur le
cercle, le triangle
isocèle DOE est invariant. La corde DE conserve la même longueur. |
|
|||
|
Brèves associées |
>>>
Triangle
inscrit dans le rectangle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Démonstration de cette propriété |
>>>
Deux cercles dans un carré |
||
959. Congruence des puissances |
|
|||
|
Propriété Si deux nombres, divisés par m, ont le même
reste, alors les puissances k de ces nombres, divisées par m, auront même
reste (un autre). On note (deux façons)
On lit Si a et b sont "égaux" (noté avec trois traits) modulo m alors ak
et bk sont aussi congruents (ont le même reste) modulo m, quelle que soit la valeur de k. Exemples
|
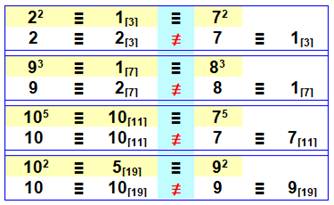
RÉCIPROQUE Si les puissances sont congruentes, les nombres
eux-mêmes ne sont pas forcément congruents modulo m. Cas détaillé montrant que la
propriété ne s'inverse pas
Autres exemples de congruences avec
des puissances (dont celui ci-dessus).
|
|||
|
Brèves associées |
>>>
Consécutifs
– Divisibilité de la somme |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Congruences – Formules |
>>>
Structures algébriques |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()