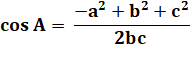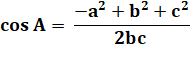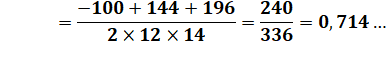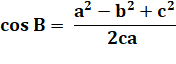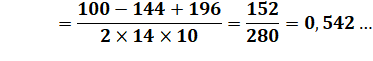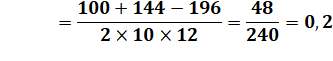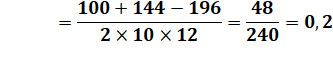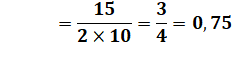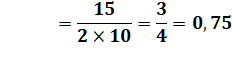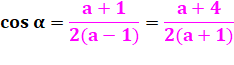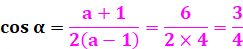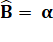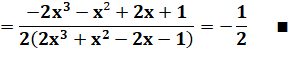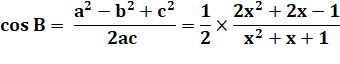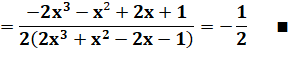![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For this page,
refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Résolution LLL des triangles
Cas
où la longueur des trois côtés
est connue. La loi des cosinus permet de calculer la valeur
des angles. Exemples
de calculs. |
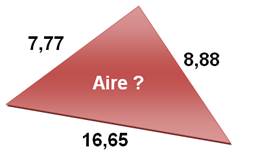
Énigme
|
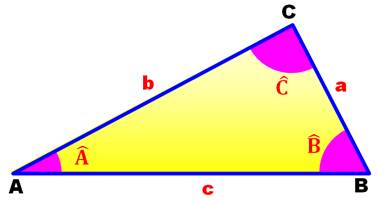
Si on connait la longueur des côtés du triangle, on
connait son aire en utilisant la formule
de Héron. Bonus, on connait aussi les angles
par la formule
de l'aire: |
Voir Exemple d'application dans le défi des trois cercles tangents
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
A = Arccos (0,714 ) = 44, 415… ° |
|
|
|
B = Arccos (0,844 ) = 57, 122… ° |
|
|
|
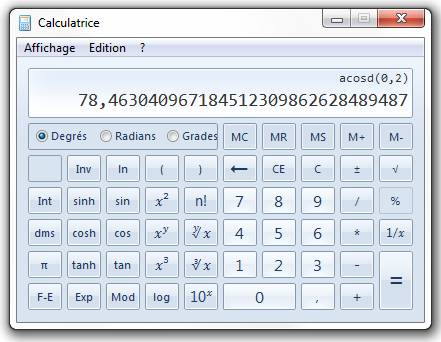
C = 180 – 44,415 – 57,122 = 78,463 … °
B = Arccos (0,2 ) = 78,463… ° |
|
|
|
|
|
|
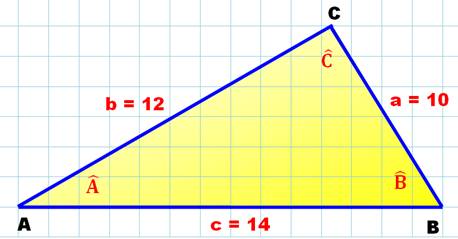
Notez la beauté du carré (3456). |
s = ½ (10 + 12 + 14) = 18 A² = s
(s – a) (s – b) (s – c) A² = 18
x 8 x 6 x 4 = 3 456 A = 58,787 |
|
|
|
||
|
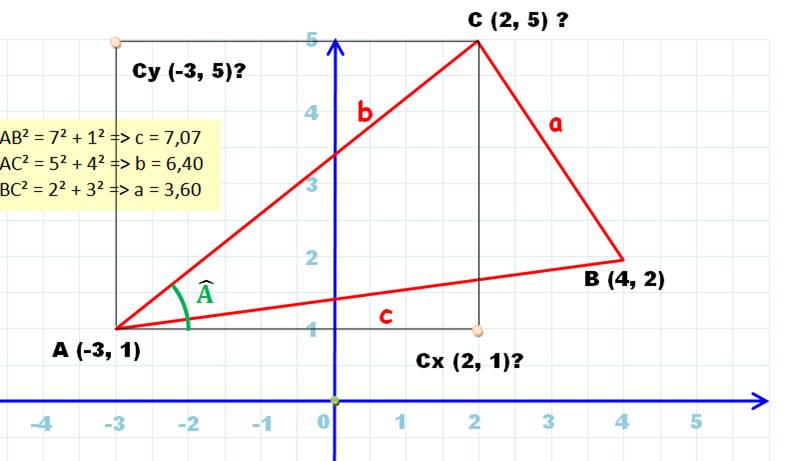
Problème Le triangle ABC
est connu par la longueur des trois côtés (a = 3,6; b = 6,4 et c = 7,07). Il est
positionné dans le plan par la donnée de deux de ses sommets A (-3, 1) et B
(4, 2). Trouvez les
coordonnées du troisième sommet C. Figure Elle est construite a priori, en connaissant les coordonnés des trois
points. On a calculé les longueurs a, b et c avec le théorème de Pythagore.
Ceci, afin de pouvoir vérifier les résultats du calcul.
Méthode 1. On calcule l'angle A, composé de deux angles dont l'un est un angle du
triangle. On le calcule à l'aide de la
loi des cosinus. 2. AC est la diagonale d'un rectangle dont on calcule les dimensions. Ce
sont les coordonnées de C par rapport au point A. 3. Calcul des coordonnées de C à partir de l'origine des axes. Calculs |
||
|
|
cos A1 = (b2 + c2 − a2) / 2bc =
(6,4²+7,07²-3,6²) / 2 x 6,4 x 7,07 =
0,862… A1
= 0,532… rad = 30,48…° |
|
|
|
tan A2 = 1/7 = 0,1428… A2 = 0,1419… = 8,13 ° |
|
|
|
A = A1 + A2 = 0,674… = 38,62…° |
|
|
|
CCy = b cos(A) = 6,4 x 0,781 … =
5,00… |
|
|
|
x de C = 5 + (-3) = 2 |
|
|
|
CCx = b sin(A) = 6,4 x 0,624 … =
3,99.. |
|
|
|
y de C = 4 + 1 = 5 |
|
|
|
||
|
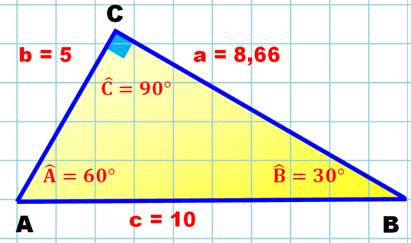
Seule la
connaissance de deux côtés suffit puisque nous connaissons un des angles, l'angle droit. Ce cas est un
cas particulier des cas LAL ou LLA. Dans le cas où
trois côtés seraient donnés, il faudrait vérifier que a² + b² = c² pour être
sur que le triangle est rectangle. |
Dans le cas de ce triangle rectangle, un côté est
le double de l'hypoténuse. Les deux autres angles sont égaux à 30° et 60°. On vérifie que 10² – 5² = 75 et sa racine vaut
8,66025… Aire = 21,6506… |
|
|
|
||
|
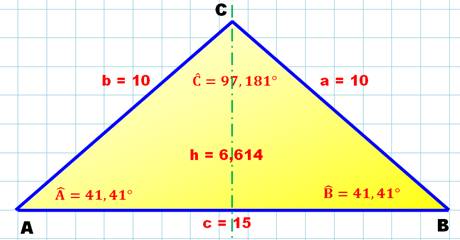
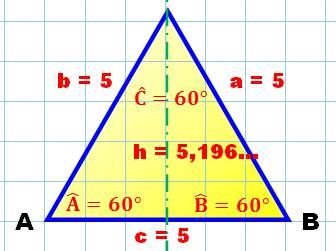
Cas particulier
de notre cas LLL avec deux côtés de même longueur. La loi des cosinus n'est à
appliquer qu'une seule fois. Notez comment se
simplifie la formulation de la loi du cosinus. |
A = B = Arccos (0,75 ) = 41, 4096… ° Aire = 49,6078… |
|
Voir Triangle 456 avec
angle de 41,41°
|
|
||
|
Dans ce cas, il
suffit d'une seule mesure: la longueur du côté. |
Aire = 15,5884… |
|
|
|
||
|
Exemple
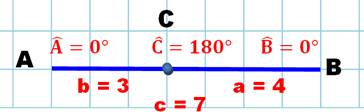
avec triangle 347 L'inégalité
triangulaire nous apprend que la somme de deux longueurs ne peut pas être
inférieure à la troisième. Si
la somme est égale au troisième côté, le triangle est réduit à un segment de
longueur égale à 7. Cas
du triangle 123. La
somme de deux côté est égale au troisième. Le triangle est réduit à un
segment de longueur égale à 3. |
C'est un triangle dégénéré en segment. L'angle en C est un angle plat et les deux autres sont nuls. |
|
|
|
||||
|
On
connaît le triangle
rectangle remarquable de côté 3, 4 & 5. Ici,
on cherche, un triangle
Résolution |
|
|||
|
|
|
|||
|
Calcul |
|
|||
|
Bilan |
|
|||
|
|
||||
|
Calcul |
|
|||
|
Égalité
entre les deux valeurs du cosinus |
|
|||
|
Calculs |
(a + 1)² a² + 2a + 1 2a + 1 a |
= (a + 4) (a – 1) = a² + 4a – a – 4 = 4a - a - 4 = 5 |
||
|
Solution |
b = a – 1 a c
= a + 1 |
= 4 = 5 = 6 |
||
|
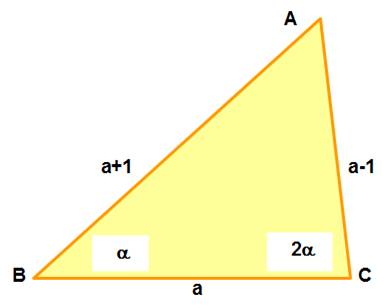
Extraordinaire |
Le triangle 4, 5 & 6 est remarquable. Il a un angle double de l'autre. Quelle est
sa valeur ? |
|||
|
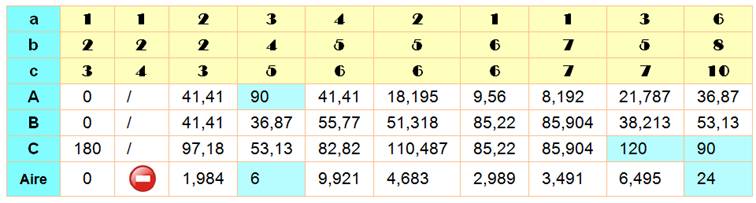
Valeur
des angles et
calcul de l'aire |
Aire = 9,92156… |
|||
|
|
|||
|
|
a = x² + x + 1 b = 2x + 1 c = x² – 1 |
||
|
|
|
||
|
|
cos 120° = -1/2 |
||
|
|
|
||
|
|
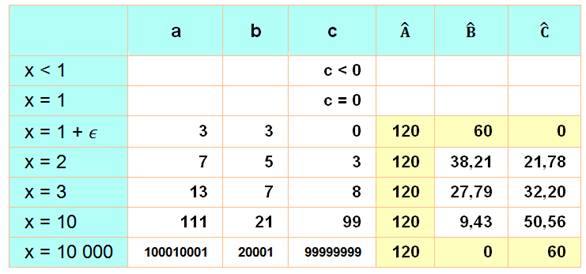
Ces formes conduisent à des angles non
remarquables |
||
|
|
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()