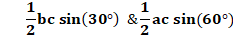énigme du carré et triangle équilatéral

Édition du: 18/12/2024

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Carré en 8, 10
	Carré oblique	Carré et triangle équil.	Défis divers
	Cercle et demi-cercle	Trois cercles tangents	Triangles dans triangle
	Triangle dans carré	Carré divisé	Deux carrés barrés

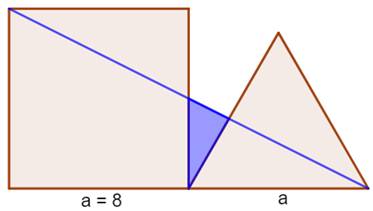
Carré et triangle équilatéral

Quelle est l'aire du triangle intermédiaire ? Comment aborder ce problème ? Identification des pistes.

Sommaire de cette page

>>> Carré et triangle équilatéral (général)

>>> Carré et triangle équilatéral (numérqiue)

Débutants

Géométrie

Glossaire

Géométrie

Carré et triangle équilatéral (général)		haut
*Une figure simple, un raisonnement pas évident à trouver. Sauf à se souvenir de la formule de* *l'aire du triangle quelconque* *connaissant deux côtés et l'angle qu'ils forment.*
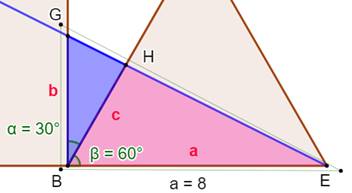
Construction Un carré de côté a et un triangle équilatéral aligné de côté également a. L'oblique bleue délimite le triangle bleu. Quelle est l'aire de ce triangle ? Piste L'angle en B du triangle bleu vaut: 90° – 60° = 30° L'aire du triangle bleu est égale à: A = ½ BH × BG × sin 30° = ¼ BH × BG Comment calculer ces deux longueurs ? Calcul de BH Le point B est le milieu du segment AE et le segment BH est parallèle au segment AD. Les triangles ADE et BHE sont semblables: BH = a / 2. Soit l'aire cherchée et les calculs qui s'ensuivent.	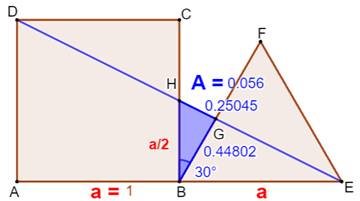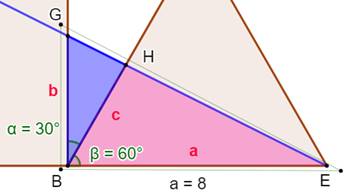Figure initiale Le côté du carré est coupé en son milieu. Figure avec notations Triangle rectangle BHE: aire connue; Triangle BNG: angle et côté connu; Triangle BGE: angle et côté connu; Application du calcul de l'aire avec le sinus de l'angle pour ces deux derniers triangles. Figure cotée avec a = 1

Carré et triangle équilatéral (numérique)		haut
*Même démonstration avec application numérique directe (a = 8 cm)*
Problème Un carré de côté a = 8 cm et un triangle équilatéral aligné de 8 cm de côté L'oblique bleue délimite le triangle bleu. Quelle est l'aire de ce triangle ? Piste Théorème de Pythagore? Pourquoi pas dans les triangles rectangles. Identification de triangles semblables? Toujours avec les triangles rectangles. Ces deux pistes laissent de côté l'intersection de l'oblique bleue avec le côté du triangle. Plus prometteur: Du fait que l'angle du triangle équilatéral vaut 60°, l'angle bas du triangle bleu vaut 30°. Bonne pioche ! Exploitons cette idée. Les trois triangles Aire de BGH = Aire de BGE – Aire de BHE Parmi leurs côtés a est connu (8 cm). Quant à b, on verra que sa valeur est 4. On sait que l'aire du triangle rectangle BGH: vaut: ½ ab = 16. Pour les deux autres, un des angles est connu leurs aires peuvent être calculées avec: Voyons le détail.	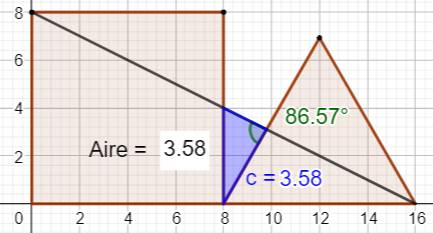Quelle est l'aire du triangle bleu ? 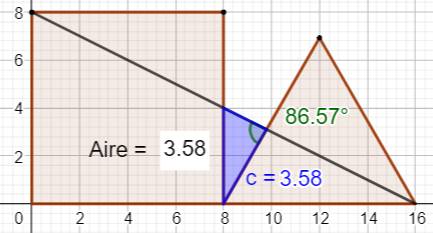Identification des trois triangles Notez que l'angle en H n'est pas un angle droit ! Il vaut 86,57°
Calcul de l'aire du carré bleu

Validation avec GeoGebra

Voir GeoGebra

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x⁴ Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Site	Find area of Green shaded Triange / Square and Equilateral triangle – Premath.com
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CarreTrg.htm