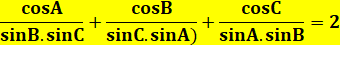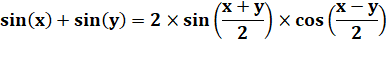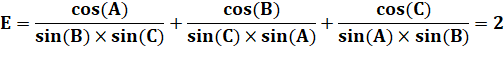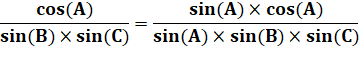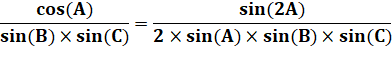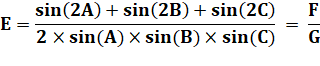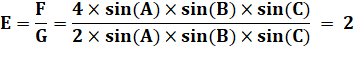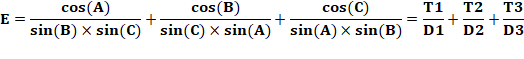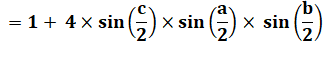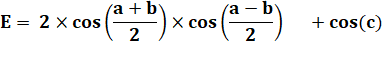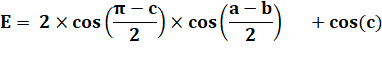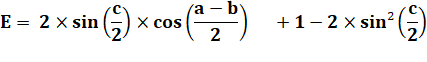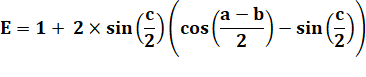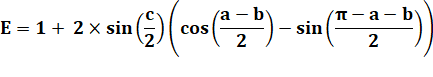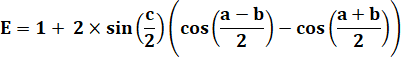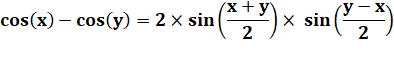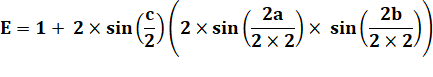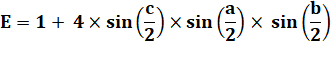NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/08/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TRIANGLES
Débutants Triangle	Résolution					Glossaire Triangle
INDEX Résolution Triangle	Résolution	Trois côtés (LLL)		Deux côtés (LAL)	Un côté (ALA)
	Formules	Trois angles (AAA)		Deux côtés (LLA)	Un côté (AAL)
	Formules avancées			T 13 14 15
	Terminale		Sommaire de cette page >>> Trigo dans le triangle quelconque (1) >>> Trigo dans le triangle quelconque (2) >>> Trigo dans le triangle quelconque (2bis) >>> Trigo dans le triangle quelconque (3)

Formules avancées dans

le TRIANGLE QUELCONQUE

Plusieurs formules démontrées.

La première permet la démonstration de la seconde, et la seconde montre que tout triangle quelconque recèle le nombre 2.

Forme texte: (cos(A))/(sin(B)×sin(C))+(cos(B))/(sin(C)×sin(A))+(cos(C))/(sin(A)×sin(B))=2

Trigo dans le triangle quelconque (1)
Prouvez que dans un triangle quelconque:
Formules d'addition.
Avec x = 2A et y = 2B
Avec 2C =:
Angles du triangle.
Angles supplémentaires.
Revenons à T:
Mise en facteurs:
Angles du triangle.
Formules d'addition
Finalement:

Merci à Claude M. pour sa relecture attentive

Trigo dans le triangle quelconque (2)
Prouvez que dans un triangle quelconque:
Premier terme multiplié par sinA.
Formule angle double.
Remplacement:
Idem pour les deux autres termes et remplacement dans E.
On s'intéresse à F pour démontrer qu'il vaut 2G.
Formule déjà démontrée.
Finalement:

Trigo dans le triangle quelconque (2 bis) Démonstration avec les mesures des côtés
Prouvez que dans un triangle quelconque:
Démarche	Calcul des sinus et cosinus en fonction des côtés et de R. Calcul de R en fonction de S, puis de S en fonction des côtés.
Formule des sinus avec R rayon du cercle circonscrit
Expression des sinus (écriture simplifié)
Expression des cosinus
Expression des dénominateurs
Expression de E
Passage à l'aire S
Retour à E réduite
Retour à E développée (tous calculs faits et profitant de a²b²c² au numérateur)
Avec la valeur de l'aire, on calcule S²
S² développé (tous calculs faits)
Cette valeur dans E

Pour les formules de bases voir: Relations dans le triangle quelconque / Formules trigonométriques

Trigo dans le triangle quelconque (3)
Prouvez que dans un triangle quelconque:
Formule d'addition.
Angle dans le triangle (180°).
Angle moitié.
Mise en facteur:
Angle dans le triangle.
Angles complémentaires.
Addition trigo.
avec x = (a-b)/2 et y = (a+b)/2:
Finalement:

Merci à Michel S. pour l'idée de cette page

Retour	Relations fondamentales dans le triangle quelconque
Suite	Résolution du triangle LLL (trois côtés connus) Formule de Héron Aire de la projection des triangles Relations trigonométriques – Formulaire Calculs trigonométriques – Exercices
Voir	Cercle Géométrie Polygone Triangle - Index Triangle – Introduction Trigonométrie
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/RelQuelA.htm