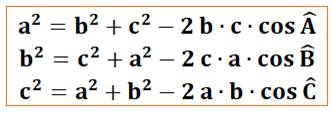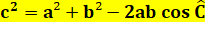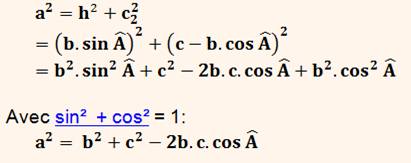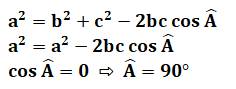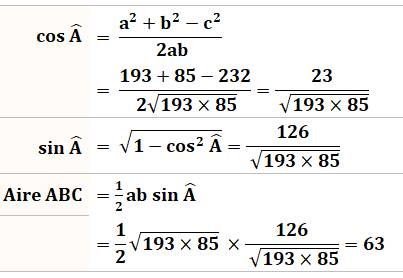Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 27/08/2023 M'écrire Brèves de Maths

INDEX Résolution Triangle	Triangles – Relations
	Résolution	Formules	Loi des sinus	Loi des cosinus
	Formules avancées		Hypoténuse

Triangles – Loi des COSINUS Formule d'Al Kashi Généralisation du théorème de Pythagore Belles proportions entre les longueurs des côtés du triangle et les cosinus de ses angles.
	Sommaire de cette page >>> Loi des cosinus >>> Démonstration >>> Réciproque du théorème de Pythagore >>> Exemple: deux côtés et leur angle >>> Exemple avec triangle en racines	Débutants Triangles Glossaire Triangles

Loi des cosinus			haut
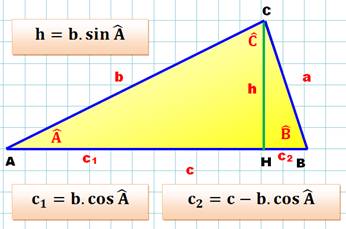
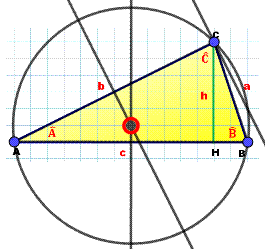
Triangle Un triangle quelconque ABC. Notations usuelles des angles et des côtés. Une des hauteurs h qui crée les segments AH = c1 et HB = c2. Loi des cosinus
Applications	Pratique pour calculer Le troisième côté en connaissant deux côtés et leur angle; ou les angles lorsqu'on connaît les trois côtés.

Démonstration		haut
Démonstration avec Pythagore Théorème de Pythagore dans le triangle rectangle BCH:

Pour info: Triangle rectangle ?

Jean-Marc signale que le triangle jaune ci-dessus est sans doute un triangle rectangle. Vérifions, en supposant qu'il est rectangle:

a² = 6² + 2² = 40 => a = 6,324 …

b² = 6² + 12² = 180 => b = 13,416…

c² = 6,324² + 13,416² = 220 => 14,832…

Or le valeur mesurée sur la figure est 14

Le triangle n'est pas exactement rectangle, mais pas loin.

Effectivement la perpendiculaire en C à AC coupe AB à une unité plus loin avec AB = 15. En reprenant le calcul ci-dessus, on trouve bien AB = 15.

Le cercle circonscrit au triangle ABC a son centre (rouge) une unité au-dessus de AB et la distance de ce centre aux sommets est de 7,07… unités (= racine de 50).

Voir Construction d'un triangle quelconque, pas si évident!

Démonstration (Suite)		haut
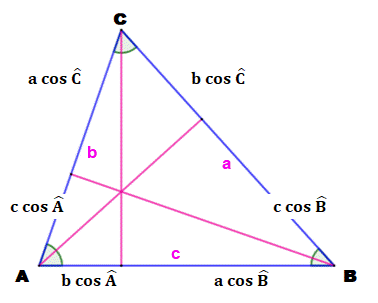
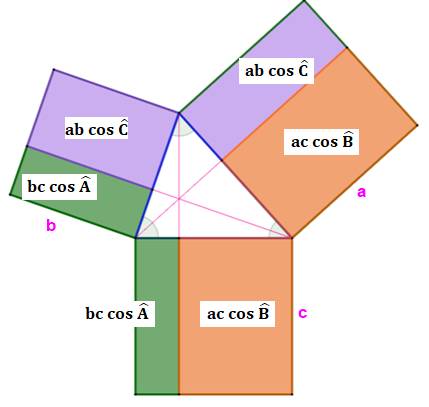
Démonstration sans Pythagore La figure du haut montre le triangle avec ses hauteurs. On indique la longueur des segments découpés par les pieds des hauteurs. Sur la figure du bas, on a flanqué des carrés sur les côtés du triangle. Lesquels sont coupés en deux parties inégales par le prolongement des hauteurs. L'aire de chacun des rectangles est répertoriée: c'est le segment de hauteur multiplié par le côté du carré. On se retrouve avec des couples de rectangles avec aires identiques (repérés par une couleur). Comparons le carré du bas aux deux autres: Aire carré bas = Aires carrés haut – Aires des deux rectangles violets. C'est le théorème de Pythagore généralisé au triangle quelconque. On retrouve bien l'identité classique pour le triangle rectangle pour lequel le cosinus de l'angle droit est nul.

Réciproque du théorème de Pythagore		haut
Réciproque du théorème de Pythagore On sait démontrer la loi des cosinus sans le théorème de Pythagore. Alors, il est légitime de démontrer que: si a² = b² + c² alors, le triangle est rectangle (angle de 90°).	Si a² = b² + c² Loi des cosinus:

Voir Calcul de l'aire des quadrilatères / Al Kashi

Calcul d'une formule donnant 2 comme invariant dans le triangle quelconque

Inverse du théorème de Pythagore

Exemple: deux côtés et leur angle		haut
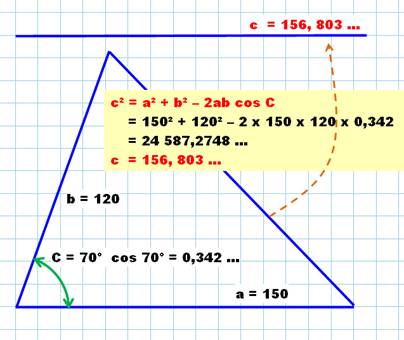
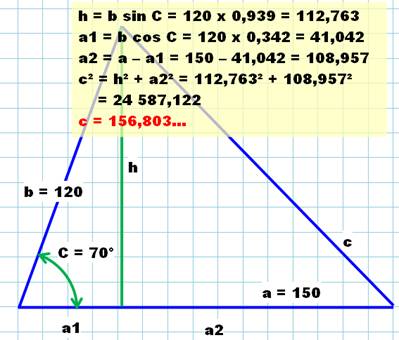
On connait: a = 150 cm, b = 120 cm, et C (angle) = 70°. Première solution en appliquant la loi des cosinus. La figure est à l'échelle (10 cm = 1 carreau). Le segment "c" est recopié en haut et mis à l'horizontale. Sa mesure permet de vérifier le calcul. Seconde solution avec trigonométrie et Pythagore. Calcul de proche en proche pour atteindre "c"

Voir Résolution générale de ce cas (LAL)

Exemple avec triangle en racines		haut
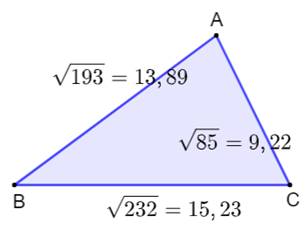
Construction Un triangle quelconque dont on connait les longueurs des côtés exprimées avec les radicaux. Calculer l'aire du triangle. Pistes La formule de Héron conduit à des calculs un peu longs. Il y a mieux: calculer le cosinus de l'un des angles (A par exemple), et utiliser la formule en sinus de l'aire du triangle.
Calculs

Haut de page

Retour	Formules dans le triangle Théorème de Pythagore sur d'autres figures que le triangle Formule du triple quad
Suite	Loi des cosinus Application au partage du cercle Formules avancées dans le triangle quelconque Formule de Héron et sa démonstration
Voir	Aire de la projection des triangles Cercle Géométrie Polygone Quadrilatère et diagonale inconnue Relations trigonométriques – Formulaire Résolution du triangle LLL (trois côtés connus) Triangle - Index Triangle – Introduction Trigonométrie
Sites	Loi des cosinus – Wikipédia The Law of Cosines – Cut-the-knot – A. Bogomolny Law of Cosines – Wolfram MathWorld Proof of the Law of Cosines – Math Open Reference
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/LoiSinus.htm