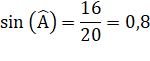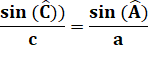Résolution du triangle LLA, deux côtés et un angle

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/05/2017 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TRIANGLES
Débutants Triangle	Résolution				Glossaire Triangle
INDEX Résolution Triangle	Résolution	Trois côtés (LLL)	Deux côtés (LAL)	Un côté (ALA)
	Formules	Trois angles (AAA)	Deux côtés (LLA)	Un côté (AAL)
		Sommaire de cette page >>> Méthode pour le triangle quelconque >>> Exemple >>> Triangles rectangle >>> Triangle isocèle >>> Triangle équilatéral >>> Tableau d'exemples

Résolution LLA des triangles

Sont connus deux côtés et un angle.

Méthode et exemples de calculs.

Ce cas est particulier par le fait qu'il peut induire deux solutions.

Méthode pour le triangle quelconque

La loi des sinus pour le calcul d'un deuxième angle

La somme de 180° pour trouver le troisième angle.

La loi des sinus pour le calcul du troisième côté

Exemple: LLA = {10, 40°, 15}
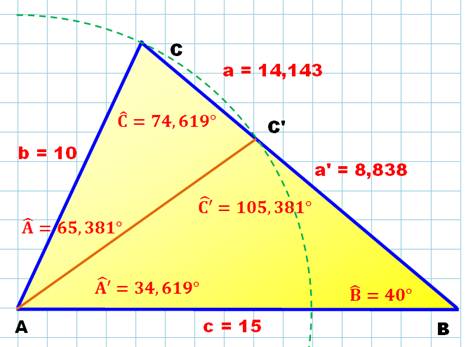
On connait: b = 10 c = 15 Angle en B = 40° La construction de la figure montre que deux triangles sont possibles. Le cercle en pointillé vert indique une distance de 10 à partir du point A. La droite BC, à 40° par rapport à AB, coupele cercle en deux points C et C'. Soit les deux triangles ABC et ABC'.
Loi des sinus pour l'angle en C C'est ici qu'apparaît la seconde solution. Les angles C et C', son supplémentaire, ont le même sinus. Le meilleur moyen de s'en rendre compte est de faire la figure à l'échelle, même approximative.	= arcsin(0,964) = 74,61856… = 180° – C = 105,381…°
Troisième angle	= 180 – 40 – 74,6186 = 65,3814…°
Loi des sinus pour le côté a
Calcul de l'aire avec la formule de Héron, s étant le demi-périmètre.	s = ½ (10 + 15 + 14,143) = 19,571 A² = s (s – a) (s – b) (s – c) A = 68,18258…

Triangle rectangle
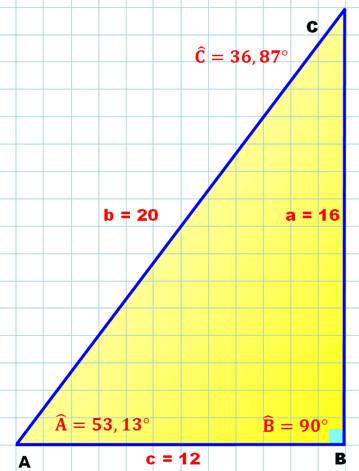
Cas particulier où l'angle est droit. Nous connaissons: b = 20 c = 12 angle en B = 90° Nous sommes typiquement dans le cadre d'application du théorème de Pythagore: connaissant deux côtés, le troisième s'en déduit immédiatement
Longueur du troisième côté	a² = b² - c² = 400 – 144 = 256 a = 16
Angle en A	= arcsin(0,8) = 53,1301 …
Angle en C	= 180 – 90 – 53,1301 = 36,869897 …
Aire du triangle rectangle	A = ½ (12 x 16) = 96

Triangle isocèle
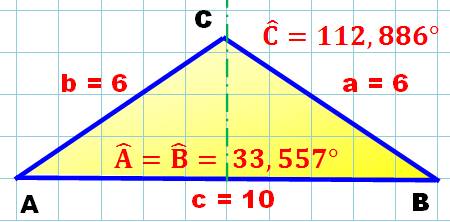
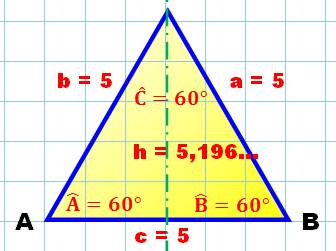
Pour résoudre le triangle isocèle, la connaissance d'un côté et d'un angle suffit. Nous connaissons: c = 10 Angle en B = 33,557°
Angles	= 180 – 2 x 33.557 = 112,886°
Loi des sinus pour le côté c
Hauteur issue de C	h² = 6² - 5² = 11 h = 3,316…
Aire	A = ½ c . h = 5 x 3,316 16,5831…