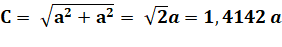|
||||||||||||||||||||||||||||||||||||||||
|
TRIANGLES RECTANGLES LONGUEUR de l'HYPOTÉNUSE Méthode TAMOULE |
|
|
Nous
allons voir trois méthodes de calcul avec:
|
Tu as
sans doute raison, Pythagore. Mais, tout le monde va rire si tu l'appelles hypoténuse. |
Hypoténuse:
du grec hypo, préfixe signifiant: sous; et
teinousa, participe présent de tendant.
Anglais: hypotenuse; Italien: ipotenuzo
Quelques
triangles rectangles typiques et leur hypoténuse
Voir Triangles
rectangles typiques
|
|
|||
|
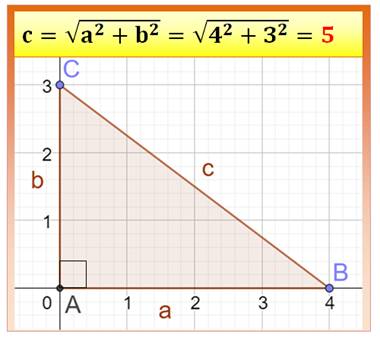
La
longueur de l'hypoténuse d'un triangle rectangle est calculée facilement si
on connait la longueur des deux autres côtés (dits base et hauteur). Il
suffit d'appliquer le théorème
de Pythagore. Ce calcul
implique le calcul d'une
racine carrée. Simple avec les moyens actuels (calculette);
plus compliqué autrefois. Il se
trouve qu'avec les nombres de la figure (3 et 4), l'hypoténuse est mesurée
par un nombre entier. De telles
situations sont fréquentes; il s'agit des triplets
de Pythagore. |
|
||
|
Évidemment, le
calcul est tout aussi faisable avec des longueurs non entières. Les mesures notées à droite sont celles relevées
sur un dessin réalisé avec le logiciel gratuit Geogebra. |
|
||
|
|
||
|
La définition du
sinus est appliquée. On aurait pu
faire la même chose avec les cosinus |
|
|
|
Résolution
générale du triangle dans le cas particulier où il est rectangle. Voir pages
spéciales >>> |
||
Méthode sans calcul de racine
carrée (approximation)
|
|
||
|
Texte Tamoul Odum
Neelam Thanai Ore Ettu Kooru thaaki Koorilae Ondrai Thalli Kundrathil
Paadhiyai Saerthal Varuvathu Karnam Thane. Le texte est un quatrain rédigé par
Bothainayanar, sage et mathématicien tamoul (information à vérifier). Tamouls: peuple de l'Inde du sud et Sri Lanka. La langue tamoule, apparue il y a plus de 2500
ans, est l'une des plus anciennes langues du monde encore parlées
aujourd'hui. Traduction
|
Avec les
notations classiques
|
|
|
Théorème de
Pythagore La valeur
exacte est obtenue avec cette formule attribuée à l'école de Pythagore, mais
connue des Babyloniens. |
|
|
|
|
|||
|
Triangle rectangle (8, 6) La formule
Tamoule donne 10 cm alors que la valeur exacte obtenue avec le théorème de
Pythagore est 10 cm. Avec ce triplet
de Pythagore classique (3,4, 5 multiplié par 2), la formule Tamoule évalue exactement la longueur de l'hypoténuse. Le rapport entre
longueurs des côtés: 6/8 = 3/4. Nous verrons que ce rapport est important pour
caractériser la précision de la formule. |
|
||
|
Triangle rectangle (16, 8) La formule
tamoule donne 18 cm alors que la valeur exacte obtenue avec le théorème de
Pythagore est 17,88 cm. Erreur relative
de:
Le rapport entre
longueurs des côtés: 16/8 = 2. |
|
||
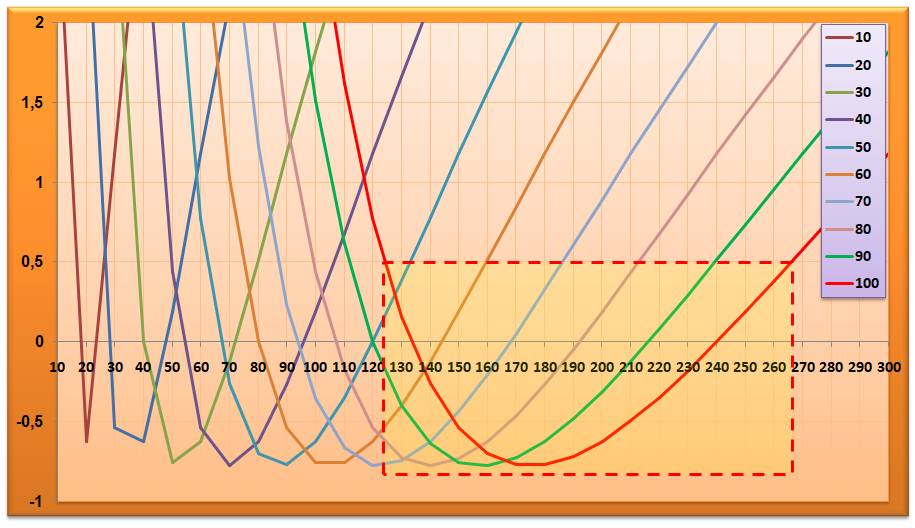
Précision
relative en % en fonction de a et selon diverses valeurs de b (de 10 en 10)
Abscisse a; réseau de
courbes pour b et rapport en ordonnées
|
|
|||||
|
Calcul Prenons a
comme proportion de b: a = kb avec k > 1. On
calcule le rapport R entre les deux évaluations de la longueur de
l'hypoténuse. |
|
||||
|
Cas où a = b En cas de
triangle rectangle isocèle (a = b), la précision de la formule tamoule n'est
que de 2,8%. Cela revient à prendre une approximation de racine de 2 valant 11/8. |
|
||||
|
Développement
en série de R Avec ce développement,
il est curieux d'y retrouver les deux fractions de la formule tamoule. |
|
||||
|
Résolution de
l'équation Quelle
est la relation entre a et b pour que le rapport soit exactement égal à 1.
Autrement-dit: que la formule tamoule donne la valeur exacte de la longueur
de l'hypoténuse. Par le
calcul, nous retrouvons les valeurs expérimentales que nous avons observées plus haut. Et ce
sont les paires engendrant deux triplets de Pythagore |
|
||||
|
Conclusion |
La méthode tamoule donne la longuer exacte de
l'hypoténuse pour toutes les longueurs du type: b = 3/4 a et b
= 5/12 a. |
||||
|
Justification Triplets
de Pythagore génériques exprimés avec la formule tamoule. Selon ce
calcul La
méthode tamoule est rigoureuse pour les triplets de Pythagore en m = 3n et
m = 5n |
m² + n², m² – n² et 2mn m² + n² = 7/8 (m² – n²) + mn m² – 8mn + 15n² = 0 (m – 3n)(m – 5n) = 0
|
||||
|
On trouve
bien nos deux triplets en calculant a, b et c avec les valeur de m et n: |
|
||||
|
La méthode est astucieuse et assez
précise surtout au voisinage des deux rapports a/b = 4/3 ou 12/5. Le graphe du rapport en fonction de k
montre les deux coupures à 100 à 4/3 et 12/5. Le rectangle en pointillés
rouges montre la plage de précision à 0,5%.
Graphe rapport
entre les longueurs en fonction de k = a/b
Exemples proches
des racines et valeurs de plus de plus éloignées
La formule tamoule est efficace pour des
triangles rectangles bien proportionnés (a et b peu différents) |
Merci
à Jean-Paul Mercier pour sa contribution
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/Hypotenu.htm
|
