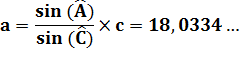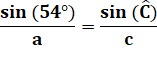Résolution du triangle AAL, deux angles et un côté

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/05/2017 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TRIANGLES
Débutants Triangle	Résolution				Glossaire Triangle
INDEX Résolution Triangle	Résolution	Trois côtés (LLL)	Deux côtés (LAL)	Un côté (ALA)
	Formules	Trois angles (AAA)	Deux côtés (LLA)	Un côté (AAL)
		Sommaire de cette page >>> Méthode pour le triangle quelconque >>> Exemple >>> Triangles rectangle >>> Triangle isocèle >>> Triangle équilatéral >>> Tableau d'exemples

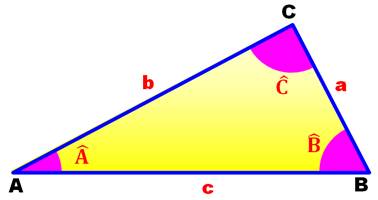
Résolution AAL des triangles

Sont connus deux angles et un côté.

Exemples de calculs.

Méthode pour le triangle quelconque

La somme égale à 180° pour trouver le troisième angle.

La loi des sinus pour le calcul des deux autres côtés.

Exemple: AAL = {25°, 55°, 15}
On connait: c = 15 Angle en B = 25° Angle en C = 55°
Troisième angle	= 180 – 25 – 55 = 100°
Loi des sinus pour le côté b
Loi des sinus pour le côté a
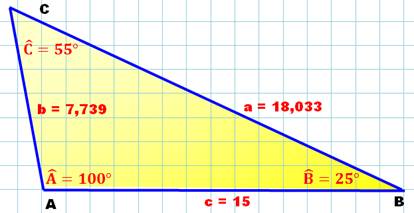
Calcul de l'aire avec la formule de Héron, s étant le demi-périmètre.	s = ½ (15 + 7,739 + 18,033) = 20,386 A² = s (s – a) (s – b) (s – c) A² = 3267,1979 A = 57,15940…
Calcul de l'aire avec la trigonométrie (Calculs exécutés avec la précision suffisante).	A = ½ a.b sin (C) = ½ x 18,0334 x 7,739 x 0,819 = 57,15940… A = ½ b.c sin (A) = ½ x 7,739 x 15 x 0,984 = 57,15940… A = ½ a.c sin (B) =1/2 x 18,0334 x 15 x 0,422 = 57,15940…
Calcul de la hauteur issue de C (exemple; idem pour les deux autres).	h = b . sin(180° – 100° ) = 7,7388 x 0,9848 = 7,6212…

Triangle rectangle
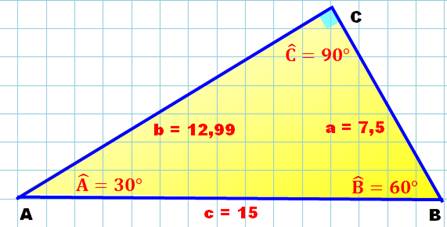
Cas particulier où l'angle est droit. Nous connaissons: c = 15 Angle en B = 60° Angle en C = 90° Nous sommes typiquement dans le cadre d'application du théorème de Pythagore: connaissant deux côtés, le troisième s'en déduit immédiatement
Troisième angle	= 180 – 90 – 60 = 30°
Côté a
Côté b
Aire du triangle rectangle	A = ½ (12,99 x 7,5) = 48,71392898…

Triangle isocèle
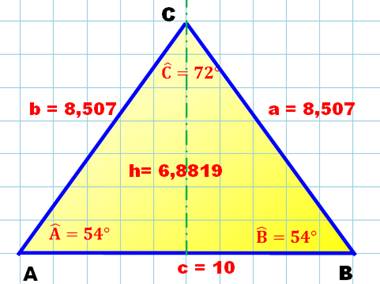
Pour résoudre le triangle isocèle, la connaissance d'un côté et d'un angle suffit. Nous connaissons: c = 10 Angle en B = 54°, ou Angle en C = 72°
Loi des sinus pour le côté a et le côté b
Hauteur issue de C	h = tan(54°) x 5 = 6,8819…
Aire	A = ½ c . h = 5 x 6,8819 = 34,4095 …