|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
HÉLICE CIRCULAIRE ou CYLINDRIQUE Longueur d'une forme hélicoïdale Calcul de la longueur d'une
hélice par la méthode du développement
de l'hélice sur un plan. |
|
|
||
|
L'hélice
est une courbe dans l'espace dont la tangente en tout point forme un angle constant avec une droite fixe. C'est
aussi le plus court chemin entre deux points sur un cylindre (hors deux points sur le même
axe). Développée à plat, l'hélice est une droite. On trouve
cette courbe sur:
|
|
|
|
Longueur de l'hélice H: longueur de l'hélice; l: la longueur d'une spire; h: hauteur du cylindre; p: le pas de l'hélice; n: la quantité de spires (h = np); r: rayon du cylindre; D son diamètre et P son périmètre (P = L'approximation est valable pour n grand ou h petit. Plus le nombre de
spires est grand sur une petite hauteur, plus la longueur de l'hélice se
rapproche de n fois le périmètre du cercle. |
Pour n spires
Pour une spire
|
|
|
Équation paramétrique Équation basée sur le fait que x et y définissent un point sur le
cercle, pendant que z lui imprime un mouvement vertical uniforme. Lorsque t = 2 |
x = r cos t y = r sin t z = c t Voir Trigonométrie |
|
|
Projections La projection d'une hélice sur un plan perpendiculaire à l'axe est un cercle. |
La projection d'une hélice sur un plan parallèle à l'axe est une sinusoïde. |
|
|
|
|
|
L'hélice
est enroulée sur un cylindre. La
méthode consiste à dérouler le fil de la spire sur un plan et appliquer le théorème
de Pythagore. Développement du
cylindre
|
|
Suite …
|
Comment
justifier le calcul indiqué ci-dessus? Prenons le cas simple d'une seule
spire et voyons ce que cela donne pour plusieurs spires. |
|
|
||
|
Sur un cylindre, une spire d'hélice
régulière. Elle part
d'un point sur le cercle du bas pour arriver au point sur le cercle d'en haut
situé sur la même verticale. De sorte que la spire fait exactement un tour. La
résolution de ce type de problème
consiste à pratiquer une coupe sur une verticale
et à développer la surface latérale du cylindre sur un plan. Imaginez que vous coupiez le cylindre le long
d'une verticale et que vous le dérouliez. Vous obtiendrez un rectangle avec
un trait oblique représentant la spire. La spire
(régulière) devient une droite et le théorème de Pythagore est
appliqué. |
Une spire sur un cylindre
L² = 10² + (6 L = 21, 33 cm |
|
|
|
||
|
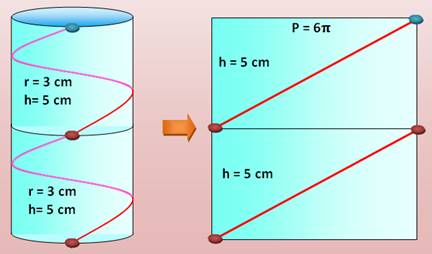
Deux spires sur deux cylindres En
empilant deux cylindres de ce type, la longueur de l'hélice (deux spires sur
20 cm) devient évidemment: 2 x 21,33 = 42,66 cm |
|
|
|
Deux spires sur un seul cylindre Si on
conserve le cylindre initial (10 cm) pour y placer deux spires, il faut
reprendre le calcul avec deux
cylindres de chacun 5 cm. Pour une spire: S² = 5² + (6 Pour deux spires: L = 2 x 19,5 = 39 cm |
|
|
|
Problème équivalent En
translatant le rectangle du haut, nous pouvons former une ligne droite
continue qui représente les deux spires de l'hélice complète. La droite
est inscrite dans un rectangle dont:
|
|
|
|
Nous
venons de montrer avec quelques dessins géométriques que la longueur de
l'hélice peut se calculer soit en calculant n fois la longueur d'une spire ou
en calculant globalement la longueur avec la formule
indiquée. |
|
|
||
|
Plusieurs spires sur un seul
cylindre La
formule de calcul devient:
Approximation
valable si n grand et h petit. Avec h =
10 cm et r = 3 cm, on obtient une bonne approximation dès n = 5 spires. Notre exemple numérique (graphes
=>) La
formule devient:
|
Courbe pour L (verte) et son
approximation (rouge)
Pour n = 5, L = 94,778 et
l'approximation vaut 94,248, soit un écart de 0,5%. |
|
|
|
|||
|
Helix; plural: helixes or helices; Sometimes: coil. |
A curve on the surface of a cylinder or cone such that its angle to a
plane perpendicular to the axis is constant; the three-dimensional curve seen
in a screw or a spiral staircase. |
||
|
Problème Un
cylindre: rayon 4 cm et hauteur 8 cm. Une
fourmi avance sur la surface du cylindre. Elle parcourt le plus court chemin
depuis un point du haut jusqu'à un point du bas, à
l'opposé. Quelle est la distance parcourue par la fourmi ? Le
cylindre peut être imaginé comme un rectangle enroulé avec une longueur de 8
cm et une largeur égale à la circonférence du cercle, soit 2 La
distance parcourue est donc:
|
Problem A
cylinder with height 8 and radius 4. An ant walks across this cylinder along
the shortest path on the curved surface from the top corner to the bottom
corner on the other side (opposite side of the cylinder). What is the
distance that the ant travels ? Your
cylinder can be thought of as a rolled up rectangle, with height 8 and width
8 |
||
Voir Anglais,
le bagage minimum
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()