somme des chiffres des nombres à une puissance

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/05/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Chiffres
Débutants Nombre	Chiffres et opérations				Glossaire Chiffres
INDEX Narcissiques Somme-Produit Ch Formes et motifs Nombres en chiffres Chiffres Sommes de nombres Types de nombres Jeux et énigmes	Somme des chiffres		Produit des chiffres	Somme + Produit
	Somme = Produit		Somme + Produit	Somme x Produit
	Somme Chiffres ^K		(Somme Chiffres) ^K	Somme Chiffres ^1,2,3…
			Couples puissants CH	Couples puissants NB
		Sommaire de cette page >>> Cas d'égalité >>> Carrés >>> Cubes >>> Bicarrés >>> Puissances 5 >>> Puissances d'un même nombre >>> Bilan

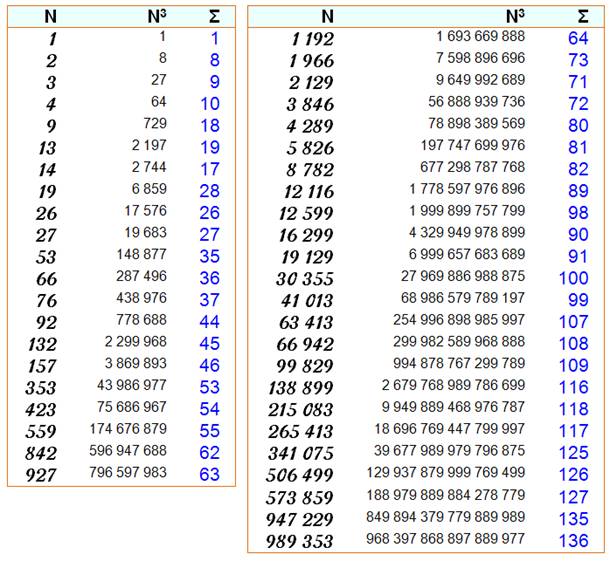
Nombres portés à une puissance.

Somme de leurs chiffres.

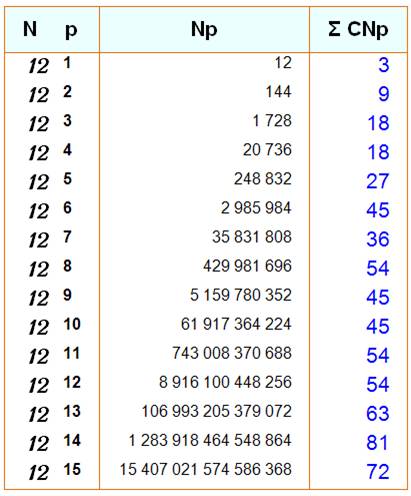
Deux types de questions concernant la somme S des chiffres d'un nombre N porté à une puissance k:

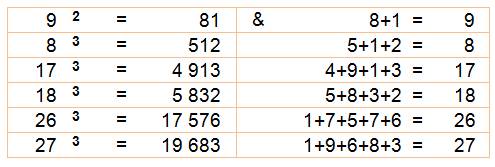
1) S = N Nombres digipuissants

Exemple: 8³ = 512 & 5+1+2 = 8

2) Quelles sont les valeurs successives de S. Ou, autrement dit: quels sont les nombres qui sont somme des chiffres de l'une de leur puissance?

Exemples: Avec les carrés: 1, 4, 7, 9, 13 …

Avec les cubes: 1, 8, 9, 10, 18 …

Voir Tous les types de nombres cousins avec ceux-ci

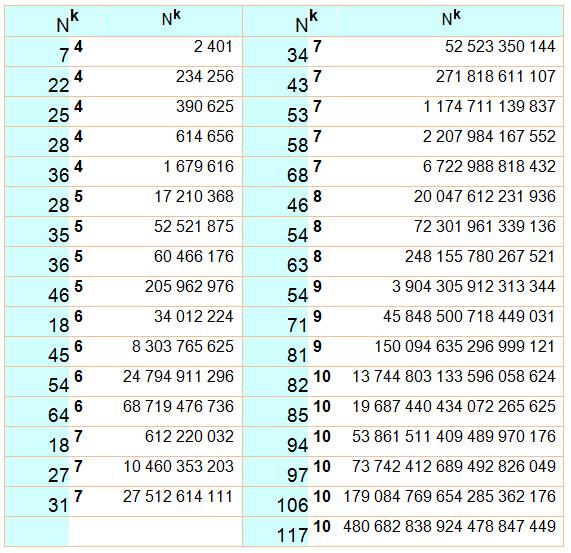
Table des nombres ayant la même somme des chiffres de leurs puissances

1) Égalités

Cas d'égalité

Nombre Égal à la Somme des Chiffres d'une de ses Puissances (NESCHIP).

Alors, il n'existe qu'un seul cas pour les carrés et cinq cas pour les cubes. Le cas trivial du 1 est éliminé (1³ =1 & 1 = 1).

Voici les 33 cas pour les puissances de 4 à 10:

Voir Les cousins / Somme de cubes / Carrés doublement carré / Cas de 27

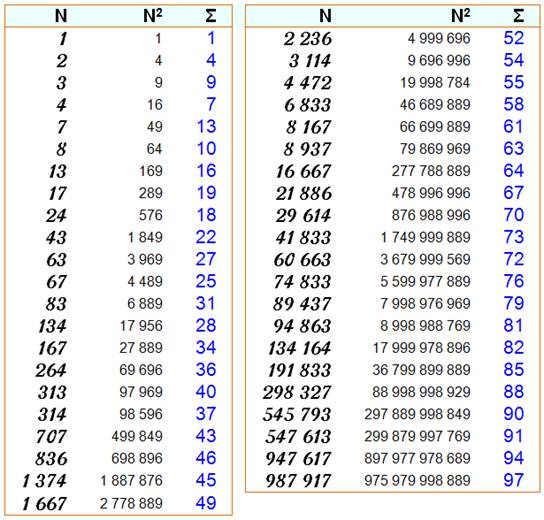
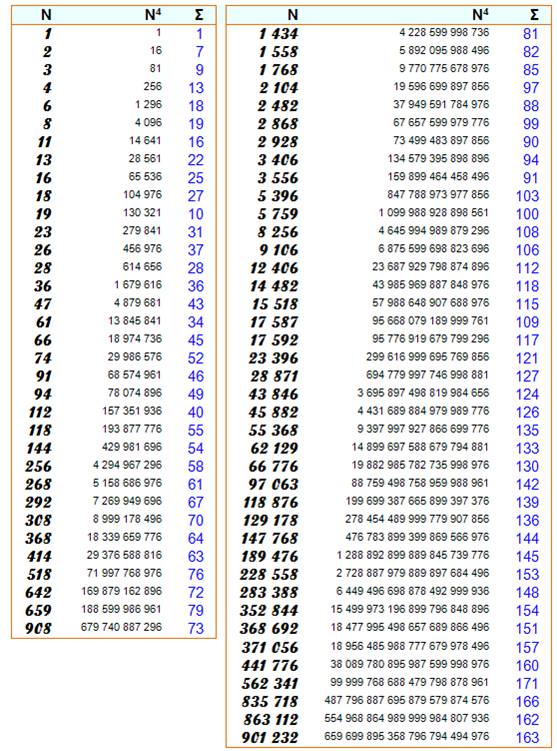
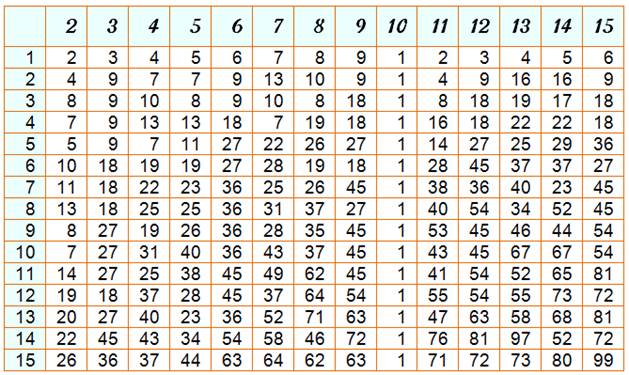
2) Valeurs successives de la somme selon la puissance

CARRÉS
Tableau donnant la liste de tous les nombres somme des chiffres d'un carré jusqu'à un million.	Exemple 2 236² = 4 999 696 4+9+9+9+6+9+6 = 52
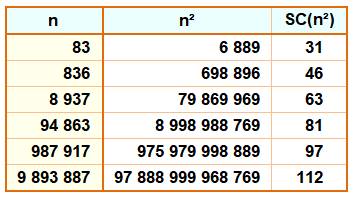
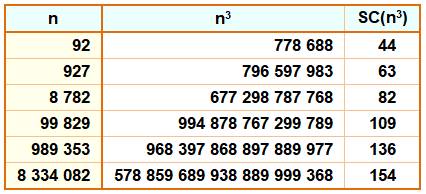
Note: une fois une somme trouvée, elle n'est pas répétée pour des nombres plus grands. Exemple: 5² = 25 & 2 + 5 = 7 qui est déjà dans le tableau avec 4² = 16 & 1 + 6 = 7. Liste ordonnée: 1, 4, 7, 9, 10, 13, 16, 18, 19, 22, 25, 27, 28, 31, 34, 36, 37, 40, 43, 45, 46, 49, 52, 54, 55, 58, 61, 63, 64, 67, 70, 72, 73, 76, 79, 81, 82, 85, 88, 90, 91, 94, 97, 99, 100, 103, 106, 108, 109, 112 jusqu'à 10⁷. Somme des chiffres du carré = 100: n = 1 643 167, n² = 2 699 997 789 889
Somme maximale par puissances de 10 Exemple: pour les nombres à trois chiffres, c'est 836 qui offre la plus grande somme de chiffres (46) avec son carré.

CUBES
Tableau donnant la liste de tous les nombres somme des chiffres d'un cube jusqu'à un million.	Exemple 13³ = 2 197 et 2+1+9+7 = 19
Voir Égalité de cubes en couples – Tableau des nombres donnant la somme 18
Somme maximale par puissances de 10 Exemple: pour les nombres à trois chiffres, c'est 836 qui offre la plus grande somme de chiffres (46) avec son carré.

BICARRÉS (Puissance 4)
Tableau donnant la liste de tous les nombres somme des chiffres d'une puissance quatrième jusqu'à un million.	Exemple 4⁴ = 256 et 2+5+6 = 13

Puissance 5
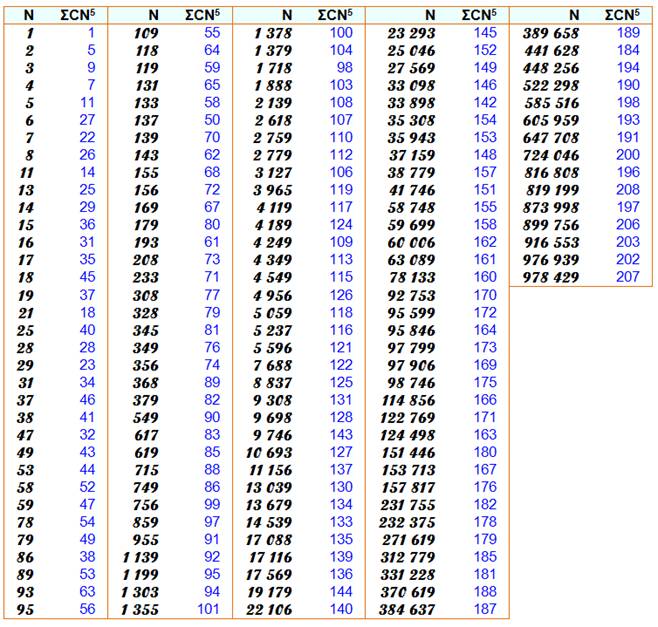
Tableau donnant la liste de tous les nombres somme des chiffres d'une puissance cinquième jusqu'à un million.	Exemple 8⁵ = 32 768 et 3+2+7+6+8 = 26
Toujours pour un million: Avec la puissance 6 le maximum est 234. Avec la puissance 7 le maximum est 279.

Puissances du même nombre

Voici le tableau des puissances de 12 avec la somme de leurs chiffres.

Ces sommes sont toutes des multiples de 9 à partir du carré.

Voici le tableau des sommes pour tous les nombres de 2 à 15 (en colonnes) et pour les puissances de 1 à 15 (en lignes). On retrouve en colonne du 12 les valeurs indiquées dans le tableau ci-dessus.

Les colonnes pour les multiples de 3 sont toutes en multiples de 9, à partir du carré.
Explication: dès que l'on multiplie 3 x 3, on obtient un 9. Dans les produits suivants (comme 3 x 3 x 3), il y a un 9 "inside". Or, la somme des chiffres des multiples de 9 sont des multiples de 9.

Bilan

Somme des chiffres d'une puissance de N égale à N: il en existe une en quantité infinie, mais les cas sont limités pour chaque puissance: 6 cas pour les carrés et les cubes.

La somme des chiffres des nombres portés à une puissance reste confinée dans un petit nombre de possibilités de 1 à M. Par exemple pour les nombres jusqu'à 1 million, la valeur du maximum M est, selon la puissance (indiquée en indice):

97₂ 136₃ 163₄ 207₅ 234₆ 279₇ …

Mais, tous les nombres de 1 à M ne sont pas atteints par une telle somme. Pour les carrés, seules 43 valeurs sur M = 97 correspondent à une telle somme.

La somme des chiffres d'un multiple de 3 porté à une puissance quelconque est divisible par 9 (effet de la preuve par neuf).

Suite	Somme des chiffres des nombres en couple Sommes des chiffres pour 666 Somme-Produit des chiffres – Index Partition des nombres en somme de puissance Table des nombres ayant la même somme des chiffres de leurs puissances
Voir	Addition Allumettes et nombres Bases de numération Chiffres à barre – Comparaison Chiffres en lettres Nombres à barres en lettres Nombres en toutes lettres Numération - historique Pannumérique Permutation des chiffres et puissances Produit repdigit Somme des chiffres de 0 à 1 million Unité des puissances
DicoNombre	Nombre 9 Nombre 12 Nombre 97
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/Somme.htm