|
Édition du: 18/11/2021 |
|
INDEX |
Types de Nombres – Motifs |
|||
![]()
|
Skinny numbers Nombres qui ne
produisent pas de retenues lorsqu'ils sont portés au carré. |
||
|
|
Sommaire de cette page >>> Définition et propriétés >>> Liste >>> Programmation |
Débutants Glossaire |
Anglais: skinny = maigre,
filiforme, fluet
Additions
et multiplications des chiffres ne produisant pas de retenue
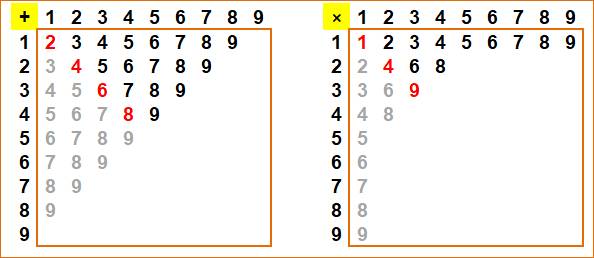
Voir Addition
/ Multiplication
|
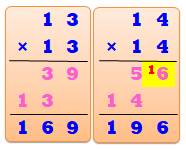
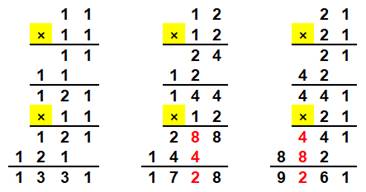
Définition classique Un nombre
fluet (skinny number) est un nombre sans création de retenue dans la multiplication par lui-même,
c'est-à-dire, lorsqu'il est mis au carré. |
|
|
|
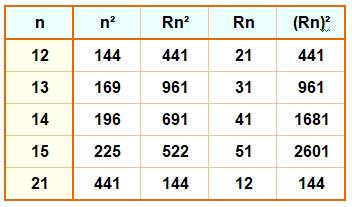
Définition équivalente Ce sont
les nombres qui sont carrément
retournés: Le retourné du carré est égal au carré du retourné R(n²) = ( R(n) )² Le tableau montre l'effet sur les nombres 12, 13
et 21 qui sont fluets et sur les nombres 14 et 15 qui ne le sont pas. |
|
|
|
Chiffres 0, 1, 2, 3 Tous les nombres fluets sont composés de [0, 1,
2, 3]. Un nombre avec des "2" ne comporte pas
de "3" et inversement. |
Le chiffre 4 On comprend facilement que le 4 est exclu de ces
nombres car 4 x 4 = 16 et occasionne
une retenue. |
|
|
Le chiffre 3 Le "3" est unique dans un nombre fluet. 30003 = 3 104 + 3 30003² = (3 104)² + (2 x 3 x 3 104) + (3²) Quelle que soit la taille d'un tel nombre, le
produit central engendre une retenue. En effet: 30003² = 900 180 009 |
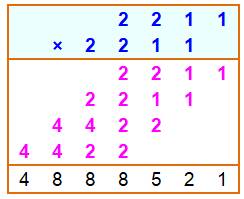
Le chiffre 2 Le "2" se présente seul ou en doublet. 2200022 = 22 105 + 22 2200022² = (22 105)² + (2 x 22 x 22
105) + (22²) Quelle que soit la taille d'un tel nombre, le
produit central engendre une retenue. En effet: 2200022² = 4 840 096 800 484 |
|
|
Il
y a 253 nombres fluets jusqu'à 100 000 1, 2, 3, 10, 11,
12, 13, 20, 21, 22, 30, 31, 100,
101, 102, 103, 110, 111, 112, 113, 120, 121, 122, 130, 200, 201, 202, 210,
211, 212, 220, 221, 300, 301, 310, 311,
1000, 1001,
1002, 1003, 1010, 1011, 1012, 1013, 1020, 1021, 1022, 1030, 1031, 1100, 1101,
1102, 1103, 1110, 1111, 1112, 1113, 1120, 1121, 1122, 1130, 1200, 1201, 1202,
1210, 1211, 1212, 1220, 1300, 1301, 2000, 2001, 2002, 2010, 2011, 2012, 2020,
2021, 2022, 2100, 2101, 2102, 2110, 2111, 2120, 2121, 2200, 2201, 2202, 2210,
2211, 3000, 3001, 3010, 3011, 3100, 3101, 3110, 3111, 10000, 10001,
10002, 10003, 10010, 10011, 10012, 10013, 10020, 10021, 10022, 10030, 10031,
10100, 10101, 10102, 10103, 10110, 10111, 10112, 10113, 10120, 10121, 10122,
10130, 10200, 10201, 10202, 10210, 10211, 10212, 10220, 10221, 10300, 10310,
11000, 11001, 11002, 11003, 11010, 11011, 11012, 11013, 11020, 11021, 11022,
11030, 11031, 11100, 11101, 11102, 11103, 11110, 11111, 11112, 11113, 11120,
11121, 11122, 11130, 11200, 11201, 11202, 11210, 11211, 11220, 11300, 12000,
12001, 12002, 12010, 12011, 12012, 12020, 12100, 12101, 12102, 12110, 12111,
12120, 12200, 12201, 12202, 13000, 13001, 13010, 13011, 20000, 20001,
20002, 20010, 20011, 20012, 20020, 20021, 20022, 20100, 20101, 20102, 20110,
20111, 20112, 20120, 20121, 20122, 20200, 20201, 20210, 20211, 20220, 20221,
21000, 21001, 21002, 21010, 21011, 21020, 21021, 21100, 21101, 21102, 21110,
21111, 21200, 21201, 21210, 22000, 22001, 22002, 22010, 22011, 22020, 22100, 22101,
22102, 22110, 22111, 30000, 30001,
30010, 30011, 30100, 30101, 30110, 30111, 31000, 31001, 31010, 31011, 31100,
31101, 31110, 31111, 100000 |
|
|
Il
y a parmi eux 63 nombres comportant un "3" Remarquez
que le "3" est unique et l'absence de "2". 3, 13, 30, 31,
103, 113, 130, 300, 301, 310, 311, 1003, 1013,
1030, 1031, 1103, 1113, 1130, 1300, 1301, 3000, 3001, 3010, 3011, 3100, 3101,
3110, 3111, 10003, 10013,
10030, 10031, 10103, 10113, 10130, 10300, 10310, 11003, 11013, 11030, 11031,
11103, 11113, 11130, 11300, 13000, 13001, 13010, 13011, 30000, 30001,
30010, 30011, 30100, 30101, 30110, 30111, 31000, 31001, 31010, 31011, 31100,
31101, 31110, 31111 |
|
|
Il
y a parmi eux 156 nombres comportant des "2" Remarquez
l'absence de "3". Les "2" peuvent être doublés mais
jamais triplés. 2, 12, 20, 21,
22, 102, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221, 1002,
1012, 1020, 1021, 1022, 1102, 1112, 1120, 1121, 1122, 1200, 1201, 1202, 1210,
1211, 1212, 1220, 2000, 2001, 2002, 2010, 2011, 2012, 2020, 2021, 2022, 2100,
2101, 2102, 2110, 2111, 2120, 2121, 2200, 2201, 2202, 2210, 2211, 10002,
10012, 10020, 10021, 10022, 10102, 10112, 10120, 10121, 10122, 10200, 10201,
10202, 10210, 10211, 10212, 10220, 10221, 11002, 11012, 11020, 11021, 11022,
11102, 11112, 11120, 11121, 11122, 11200, 11201, 11202, 11210, 11211, 11220,
12000, 12001, 12002, 12010, 12011, 12012, 12020, 12100, 12101, 12102, 12110,
12111, 12120, 12200, 12201, 12202, 20000, 20001, 20002, 20010, 20011, 20012,
20020, 20021, 20022, 20100, 20101, 20102, 20110, 20111, 20112, 20120, 20121,
20122, 20200, 20201, 20210, 20211, 20220, 20221, 21000, 21001, 21002, 21010,
21011, 21020, 21021, 21100, 21101, 21102, 21110, 21111, 21200, 21201, 21210,
22000, 22001, 22002, 22010, 22011, 22020, 22100, 22101, 22102, 22110, 22111 |
|
|
Il
y a parmi eux 32 nombres comportant des "1" sans "2" et
sans "3" Remarquez
que le "1" peut être répéter à loisir. 1, 10, 11, 100,
101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001,
10010, 10011, 10100, 10101, 10110, 10111, 11000, 11001, 11010, 11011, 11100,
11101, 11110, 11111, 100000 |
|
|
Il
y a parmi eux 39 nombres sans "0" 1, 2, 3, 11, 12,
13, 21, 22, 31, 111, 112, 113, 121, 122, 211, 212, 221, 311, 1111, 1112,
1113, 1121, 1122, 1211, 1212, 2111, 2121, 2211, 3111, 11111, 11112,
11113, 11121, 11122, 11211, 12111, 21111, 22111, 31111 |
|
|
|
Commentaires Réinitialisation générale. Procédure de retournement des nombres avec
extraction des chiffres de n à l'aide de l'instruction convert en base 10. Procédure de comparaison des nombres retournés. Programme principal qui engendre la suite (seq) des nombres fluets de 1 à 100. |
|
Voir Programmation – Index
|
Cube calculé sans retenue Outre les nombres en 1000… ou 200… (à partir de: 13
= 1 et 23 = 8), le seul nombre au cube sans retenue est 113
= 1331. Dés que l'on passe à 12 ou 21, il existe une
retenue dans la somme. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/Fluets.htm
|