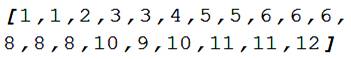|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITE Q d'HOFSTADTER Une suite originale sur le
modèle de celle de Fibonacci. Elle a été introduite par Hofstadter dans son livre célèbre:
Gödel, Bach et Escher. Nous traitons de la suite Q; il en existe d'autres
comme la suite G (Voir les références in fine). |
Douglas Richard Hofstadter (né en 1945)
|
"Tous
les vingt ou trente ans un auteur inconnu nous offre un livre dont la
profondeur, la clarté, la portée, l'humour, la beauté et l'originalité le
font immédiatement reconnaître comme un événement littéraire majeur. Gödel
Escher Bach est l'un de ces livres." Martin
Gardner, Scientific American Loi de
Hofstadter ou du glissement de
planning Il faut toujours plus
de temps que prévu, même en tenant compte de la Loi de Hofstadter. Très souvent exacte en recherche et
développement, notamment de logiciel. Voir
Loi de Murphy / Loi de Pareto |
|
|
||
|
Définition Q(1) = Q(2) = 1 Pour n > 2 : Q(n) = Q{ n – Q(n – 1) } + Q{ n – Q(n – 2) } Principe Suite du même type que celle de Fibonacci,
mais au lieu d’appeler les nombres précédents, celle-ci fait appel à un
calcul sur les rangs précédents. En fait, on ne connait pas grand-chose du
comportement de cette suite. Elle semble assez erratique ; plutôt
croissante, mais avec de nombreux retours en arrière. |
Formation Q(3)
= Q(3 – Q(2)) + Q(3 – Q(1)) = Q(3 – 1) + Q(3 – 1) = Q(2) + Q(2) = 2 Q(4)
= Q(4 – Q(3)) + Q(4 – Q(2)) = Q(4 – 2) + Q(4 – 1) = Q(2) + Q(3) = 3 |
|
|
Programme Maxima
|
Commentaires La
suite H est initialisée avec les deux premières valeurs. Boucle
d’itération en i des calculs. Calcul
des indices r1 et r2. Calcul
du nouveau nombre h. Introduction
d ce nouveau nombre dans la liste H. Impression Note : la boucle for se termine doublement avec une
parenthèse fermée et le symbole $ Résultat du traitement. Voir Programmation – Index
|
|
|
Les 200 premiers nombres de la suite Q d’Hofstadter [1, 1, 2, 3, 3, 4, 5, 5, 6, 6, 6, 8, 8, 8, 10, 9, 10, 11, 11, 12, 12, 12, 12, 16, 14, 14, 16,
16, 16, 16, 20, 17, 17, 20, 21, 19, 20, 22,
21, 22, 23, 23, 24, 24, 24, 24, 24, 32, 24, 25, 30,
28, 26, 30, 30, 28, 32, 30, 32, 32, 32, 32, 40,
33, 31, 38, 35, 33, 39, 40, 37, 38, 40, 39, 40, 39, 42, 40, 41, 43, 44, 43,
43, 46, 44, 45, 47, 47, 46, 48, 48, 48, 48, 48, 48, 64, 41, 52, 54, 56, 48,
54, 54, 50, 60,
52, 54, 58, 60, 53, 60, 60, 52, 62, 66, 55, 62, 68, 62, 58, 72, 58, 61, 78,
57, 71, 68, 64, 63, 73, 63, 71, 72, 72, 80,
61, 71, 77, 65, 80, 71, 69, 77, 75, 73, 77, 79, 76, 80, 79, 75, 82, 77, 80,
80, 78, 83, 83, 78, 85, 82, 85, 84, 84, 88, 83, 87, 88, 87, 86, 90, 88, 87, 92, 90, 91, 92, 92, 94, 92, 93, 94, 94,
96, 94, 96, 96, 96, 96, 96, 96, 128, 72, 96, 115, 100,
84, 114, 110, 93] Liste des non-Q-Hofstadter jusqu’à 100 [7,
13, 15, 18, 27, 29, 34, 36, 49, 51, 59, 67, 70,
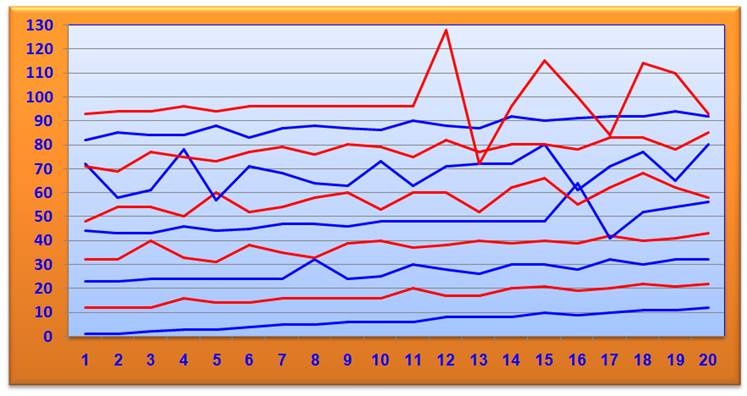
74, 81, 89, 95, 97, 98, 99] Comportement – Chaque courbe représente une tranche de 20 valeurs
|
||

![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Hofstadt.htm
|
![]()