NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Général	Formes retournées				Glossaire Général
INDEX Nombres Jeux avec les nombres	Général	Opérations palindromes		Séquences
	Proportions	Premiers		Division
	Puissances	Carré magique		Différence de carrés
	Strobogrammatique	Magie renversante		Premiers de Luhn
	Palintiple	Soustraction 99
	Carré magique	Nombres sommes de retournés
	Sommaire de cette page >>> Approche >>> Motifs complets >>> Motifs pseudo-complets >>> Résolution avec k = 4 >>> Résolution avec k = ?

Nombres retournés en proportions

Multiples complètement retournés

Nombres tels que ABC … = …CBA x k

Le nombre est divisible par son propre retourné (ou inversé).

Ils ne sont pas si nombreux !

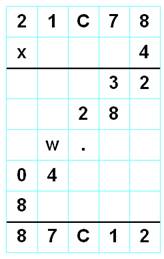
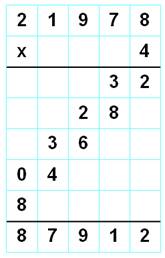
Lorsque seuls les chiffres de tête et de queue sont inversés, ce sont les nombres parasites.
Cas avec signification (alphamétique):

4 × ECART = TRACE => 4 × 21 798 = 87 912

Allez directement au problème classique avec ces nombres >>>

Devinette

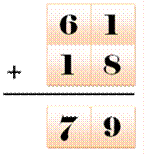
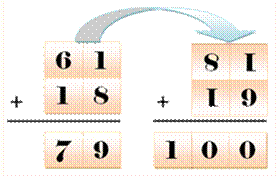
Avec ces 4 chiffres on forme une somme de 79.

Avec les mêmes chiffres, faire une somme égale à 100.

Solution

Amusement

Approche

Il s'agit de trouver des nombres tels que 8712 = 2178 x 4 Ce motif est complet car le nombre est divisible par son retourné. Ce type de motif est rare. En fait, il en existe deux familles dont les parents sont 8 712 et 9 801. 540 = 45 x 12 Ce motif pseudo-complet car c'est dix fois le nombre qui est divisible par son retourné. Ce type de motif est assez répandu. 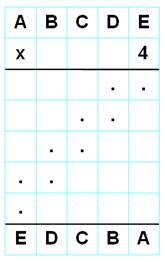Ce type de motif se retrouve dans certaines énigmes du type: ABCDE x 4 EDCBA Voir Résolution / Cryptarithme Curiosité: seuls trois nombres à trois chiffres échangent leurs unités et leurs centaines avec un de ses multiples: 208 x 4 = 832; 218 x 4 = 872; 109 x 9 = 981 Ils sont 36 à inverser les deux chiffres avec quatre chiffres: 2008 x 4 = 8032; 2018 x 4 = 8072; 2028 x 4 = 8112; 2038 x 4 = 8152; 2048 x 4 = 8192; 2058 x 4 = 8232; … 1089 x 9 = 9801; 1099 x 9 = 9891; 1109 x 9 = 9981. Ils sont 361 à inverser les deux chiffres avec cinq chiffres: 20008 x 4 = 80032; … 11109 x 9 = 99981 Suite, voir Table complète Peu de nombres inversent tous les chiffres; objet de la suite de cette page.

Seuls motifs complets
2 chiffres	Aucun
3 chiffres	Aucun
4 chiffres	Deux cas 8712 = 2178 x 4 9801 = 1089 x 9
5 chiffres	Deux cas. Les mêmes avec un 9 intercalé. 87912 = 21978 x 4 98901 = 10989 x 9

Voir Tableau en Brève de maths 434

6 chiffres	Deux cas. Un nouveau 9 intercalé. 879912 = 219978 x 4 989901 = 109989 x 9
7 chiffres	Deux cas. Un nouveau 9 intercalé. 8799912 = 2199978 x 4 9899901 = 1099989 x 9
8 chiffres	Quatre cas. Les deux cas nouveaux cas sont identiques à ceux à quatre chiffres, mais avec ces chiffres doublés. 87999912 = 21999978 x 4 98999901 = 10999989 x 9 87128712 = 21782178 x 4 98019801 = 10891089 x 9
9 chiffres	Quatre cas. 879999912 = 219999978 x 4 989999901 = 109999989 x 9 871208712 = 217802178 x 4 980109801 = 108901089 x 9

Motifs pseudo-complets (avec facteur 10)
2 chiffres	9 cas triviaux car la proportion est 10 On donne successivement N, son retourné R et le facteur multiplicatif k = N/R. 10, 1, 10 20, 2, 10 30, 3, 10 40, 4, 10 50, 5, 10 60, 6, 10 70, 7, 10 80, 8, 10 90, 9, 10
3 chiffres	Trois cas, hors triviaux (désormais omis de la liste) 510, 15, 34 540, 45, 12 810, 18, 45
4 chiffres	Onze cas, dont certains pseudo avec facteur 100, comme 2100 et son retourné 0012 devenant 12. 2100, 12, 175 4200, 24, 175 5200, 25, 208 5610, 165, 34 5700, 75, 76 En bleu, les motifs remarquables. 5940, 495, 12 6300, 36, 175 8400, 48, 175 8910, 198, 45 8712, 2178, 4 En jaune, les motifs complets. 9801, 1089, 9 Le cas de 5 700 est remarquable car le R = 75 et k = 76, deux nombres consécutifs.

5 chiffres	23100, 132, 175 27000, 72, 375 46200, 264, 175 51510, 1515, 34 Motif à 2 chiffres seulement 52200, 225, 232 52800, 825, 64 54540, 4545, 12 56610, 1665, 34 57200, 275, 208 59940, 4995, 12 65340, 4356, 15 69300, 396, 175 81810, 1818, 45 87912, 21978, 4 89910, 1998, 45 98901, 10989, 9
6 chiffres	Limité à k < 100 217800, 8712, 25 Nouveau motif 510510, 15015, 34 Idem ci-dessus, avec 0 intercalé 540540, 45045, 12 Idem ci-dessus, avec 0 intercalé 566610, 16665, 34 Idem ci-dessus, avec 0 intercalé 575700, 7575, 76 Nouveau motif 599940, 49995, 12 Idem ci-dessus, avec 9 intercalé 659340, 43956, 15 Idem ci-dessus, avec 9 intercalé 810810, 18018, 45 Idem ci-dessus, avec 0 intercalé 879912, 219978, 4 Idem ci-dessus, avec 9 intercalé 899910, 19998, 45 Idem ci-dessus, avec 9 intercalé 989901, 109989, 9 Idem ci-dessus, avec 9 intercalé
7 chiffres	2197800, 87912, 25 5100510, 150015, 34 Motifs en couple 5151510, 151515, 34 Ici avec 51 et 15 5400540, 450045, 12 5454540, 454545, 12 5604390, 934065, 6 5615610, 165165, 34 5641020, 201465, 28 5666610, 166665, 34 5705700, 75075, 76 5945940, 495495, 12 5999940, 499995, 12 6599340, 439956, 15 8100810, 180018, 45 8181810, 181818, 45 8799912, 2199978, 4 8918910, 198198, 45 8999910, 199998, 45 9899901, 1099989, 9

8 chiffres

21997800, 879912, 25 51000510, 1500015, 34 51561510, 1516515, 34 52852800, 825825, 64 54000540, 4500045, 12 54594540, 4549545, 12 56094390, 9349065, 6 56105610, 1650165, 34 56461020, 2016465, 28 56666610, 1666665, 34 56923020, 2032965, 28 57005700, 750075, 76 57575700, 757575, 76 59405940, 4950495, 12 59999940, 4999995, 12 65999340, 4399956, 15 81000810, 1800018, 45 81891810, 1819818, 45 87128712, 21782178, 4 87999912, 21999978, 4 89108910, 1980198, 45 89999910, 1999998, 45 98019801, 10891089, 9 98999901, 10999989, 9

9 chiffres

219997800, 8799912, 25 510000510, 15000015, 34 510510510, 15015015, 34 515151510, 15151515, 34 515661510, 15166515, 34 528052800, 8250825, 64 528600600, 6006825, 88 540000540, 45000045, 12 540540540, 45045045, 12 545454540, 45454545, 12 545994540, 45499545, 12 560994390, 93499065, 6 561005610, 16500165, 34 561515610, 16515165, 34 564661020, 20166465, 28 566156610, 16651665, 34 566666610, 16666665, 34 569743020, 20347965, 28 570005700, 7500075, 76 594005940, 49500495, 12 594545940, 49545495, 12 599459940, 49954995, 12 599999940, 49999995, 12 653465340, 43564356, 15 659999340, 43999956, 15 810000810, 18000018, 45 810810810, 18018018, 45 818181810, 18181818, 45 818991810, 18199818, 45 871208712, 217802178, 4 879999912, 219999978, 4 891008910, 19800198, 45 891818910, 19818198, 45 899189910, 19981998, 45 899999910, 19999998, 45 980109801, 108901089, 9 989999901, 109999989, 9

Résolution du cas classique avec k = 4

Énigme

Remplacer les lettres par des chiffres de 1 à 9 tous différents pour satisfaire la justesse de la multiplication.

Cette énigme est posée sachant que
la seule solution est 21 978 x 4 = 87 912. Le but est de trouver cette solution par le raisonnement.

Solution

Tous les produits des chiffres par 4

1	2	3	4	5	6	7	8	9
4	8	12	16	20	24	28	32	36

Tous les produits sont pairs; 4xE donne un produit pair. A est pair.

Or 4xA = E (plus retenue éventuelle). E est un nombre sans dizaines. De notre table, nous tirons que 4xA = 4 ou 8 (plus retenue éventuelle). Et A vaut 1 ou 2. Or A est pair, A vaut 2.

Du côté gauche: 4A = 8, ou 9 si retenue.

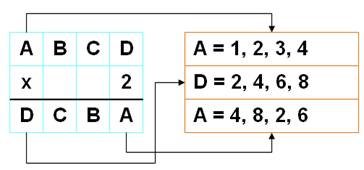
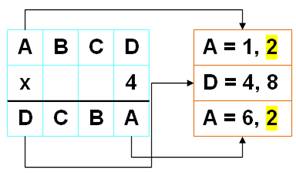
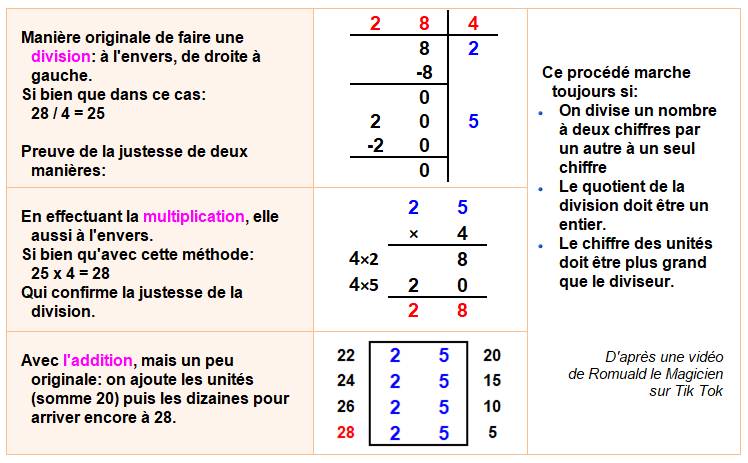
Du côté droit: 4x8 = 32 ou 4x9 = 36. Seul 32 qui se termine par A = 2 est bon.

Ce que nous savons

1	2	3	4	5	6	7	8	9
4	8	12	16	20	24	28	32	36

A est pair

A = 1 ou 2

A = 2

E = 8

Du côté gauche: 4xB ne doit pas produire de retenue pour conserver le 8 final. B = 1.

La somme 3 + v => unité 1, implique que v = 8 et que le produit 4xD se termine par v = 8; soit, 7 x 4 = 28. ce qui donne la valeur de D = 7.

1	2	3	4	5	6	7	8	9
4	8	12	16	20	24	28	32	36

La valeur pour w + 4 => unité 7, implique que w = 3

Alors 4xC = 36 seule valeur disponible dans les trentaines. Donc, C = 9.

Solution finale.

La résolution n'est pas très compliquée.
Elle aurait été un plus dure en laissant découvrir le facteur 4. On sait qu'alors, il y aurait eu deux solutions.

Notez que la recherche des solutions est grandement facilitée en posant les produits intermédiaires (cases bleues).

Résolution du cas k = ?
Nous nous contenterons de 4 chiffres; le principe est le même pour plus de chiffres. k = 1 n'est évidemment pas possible k = 2 est vite éliminé. Le principe s'appuie sur le fait que D est un nombre à un seul chiffre; ce qui limite les possibilités pour A. Alors: on dispose les valeurs possibles de A en dessous, les valeurs de D = kA puis, encore en dessous, les valeurs de kD, dont l'unité est égale à A. On cherche les cas d'égalité entre le A de départ et le A d'arrivée. k = 3, avec le même principe, ce cas est éliminé.	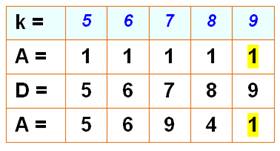D est un nombre à un seul chiffre. A ne dépasse pas 4. On compare les valeurs de A à gauche et A à droite. Aucune égalité. k = 2 est à rejeter. 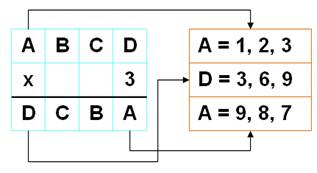Aucune égalité entre A haut et A bas; k = 3 ne marche pas.
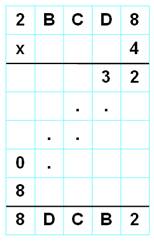
k = 4, c'est faisable La solution complète est données ci-dessus.	Bingo! A = 2 et D = 8 sont propices à une solution. On trouve: 2178 x 4 = 8712
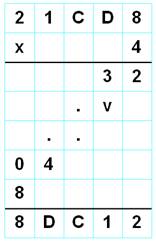
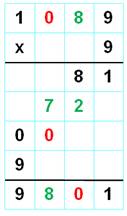
k = 5, pour conserver D à un seul chiffre A vaut 1 et D vaut 5. Alors kD = 5x5 = 25, soit A = 5. Le tableau ci-contre donne les valeurs de A initiales et finales pour k de 5 à 9. Seul le cas A= 1 et D = 9 est propice à une solution.	Avec k = 9, A = 1 et D = 9. on trouve la solution 1089 x 9 = 9801. Résolution dans l'ordre: noir, rouge et vert.

Famille qui grandit

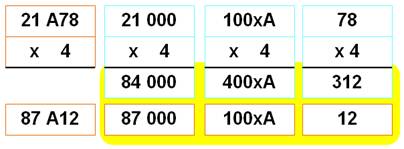
Existe-t-il un nombre A qui, placé au milieu du nombre N = 2178 et de son retourné R = 7812, conserve la même propriété de proportion: 87A12 = 21A78 x 4 Mettons cela en équations: en développant 21 A78 en bleu et 87 A12 en rouge puis en comparant les deux expressions qui doivent être égales; 84 000 + 400xA + 312 = 87 000 + 100xA + 12 300 A = 3 000 – 300 A = 10 – 1 = 9 Il existe bien une solution et elle est égale à 9. Et nous avons que la famille se poursuit indéfiniment. Ex: 2199999999999999978 x 4 = 8799999999999999912

ENGLISH CORNER
A five-digit number that, when it is quartered, gives an answer which is its digits in reverse order.

Devinette – Solution

Retour / Autres énigmes

Suite	Tables des nombres multiples à chiffres particuliers Palintiples – Compléments sur le même sujet Nombre 1089 et magie Nombres en 4 fois 4 Procédé de Kaprekar Puissances de 2 retournées Séquences avec des retournés
Voir	Factorielle Multiplication ABCDE = F x GGGGGG Nombres de Friedman Puissance Puzzles – Index
DicoNombre	Nombre 24 Accès aux autres nombres
Site	Math is fun forum (anglais)
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/RetoDiv.htm