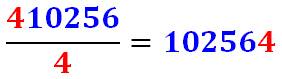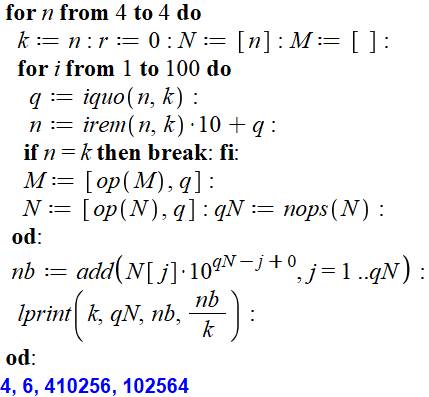|
Édition du: 24/11/2021 |
|
INDEX Division |
Itérations – Cycles |
||
![]()
|
MULTIPLICATION ou DIVISION qui retourne
Nombres
tels que divisés par le chiffre de tête produit un quotient identique, le
chiffre de tête passant en queue. Présentation
avec la multiplication: 102 564 x 4 = 410 256. |
||
|
|
Sommaire de cette page >>> Approche – Division par 4 >>> Procédé – Division par 2 >>> Divisions par k de 2 à 9 >>> Programmation >>> Retournement avec diviseur quelconque >>> Retournement inverse |
Débutants Glossaire |
|
Division Soit le nombre 410 256 et sa division par 4. Le quotient reprend les mêmes chiffres avec une permutation circulaire
plaçant le 4 de tête en queue. |
Tête
en queue
|
||
|
Observations En posant
la division, on constate que les chiffres du quotient
sont ceux qui sont abaissés lors de la division élémentaire suivante. Dit autrement et si nous ne connaissons pas ce
nombre:
|
Division
posée
|
||
http://diconombre.fr/NombDico/N1000/N400000.htm#N410000
|
But On se propose de trouver un nombre N commençant par 2 qui, divisé par
2 produit exactement les mêmes chiffres mais avec le 2 reporté en fin de
nombre. |
|
|||||
|
Procédé Sur la ligne N, inscrire le 2. Sur la ligne M, indiquer le quotient de 2 par 2,
soit 1. Le 1 est reporté sur la ligne N. Répéter ces opérations en tenant compte des restes
(R). Arrêt lorsqu'on retrouve le chiffre initial en M. Exemples 1 / 2 = 0 reste 1, le 0 est adjoint à N (=>
210); le reste est reporté en D sous la forme 10
(en rose).. 10 / 2 = 5, le 5 est adjoint à N (=> 2105). 5 / 2 = 2 reste 1, d’où le reste mentionnée en D
sous la forme du 12. Etc. |
Tableau
de formation du nombre de gauche à droite
Bilan
|
|||||
|
2 |
18 |
210526315789473684
105263157894736842 |
Avec 2,
le nombre comporte 18 chiffres. Solution
primitive unique. |
||
|
315789473684210526 157894736842105263 |
Il existe
neuf solutions pour lesquelles le nombre transféré n'est pas le diviseur (ici
3 au lieu de 2). Ce sont: Primitive
fois k/2 avec k de 1 à 9. |
||||
|
3 |
28 |
3103448275862068965517241379
1034482758620689655172413793 |
|||
|
2068965517241379310344827586 689655172413793103448275862 |
Avec chiffres
différent du diviseur, toujours neuf solutions. Ici dans le rapport k / 3. |
||||
|
4 |
6 |
Voir solutions avec chiffres différents. |
|||
|
5 |
42 |
510204081632653061224489795918367346938775 102040816326530612244897959183673469387755 |
|||
|
6 |
58 |
6101694915254237288135593220338983050847457627118644067796 1016949152542372881355932203389830508474576271186440677966 |
|||
|
7 |
22 |
7101449275362318840579
1014492753623188405797 |
|||
|
8 |
13 |
1012658227848 |
|||
|
9 |
44 |
91011235955056179775280898876404494382022471
10112359550561797752808988764044943820224719 |
|||
|
|
But Produire la liste ci-dessus. Commentaires Exploration avec n (ici uniquement 4). Initialisation des listes N et M. Boucle sans fin (ici limitée à 100). Calcul de q le quotient (iquo)
et de la valeur de R, en fait la nouvelle valeur de n le nombre à diviser. Si ce nombre est égal à la valeur de départ k,
arrêt de la recherche (break). Mise à jour des listes. En fin de traitement, calcul du nombre n en
décimal à partir de la liste N. Impression: chiffre examiné, quantité de chiffres
et nombre trouvé. |
|
Voir Programmation – Index
![]()
|
But On se propose de trouver un nombre N commençant par C qui, divisé par K
produit exactement les mêmes chiffres mais avec le C reporté en fin de
nombre. Les neuf solutions sont en fait des multiples de la première. On
retrouve la solution primitive avec k = 4. La première division est construite par le procédé
décrit ci-dessus. |
102564 / 4 = 25641 205128 / 4 = 51282 307692 / 4 = 76923 410256 / 4 = 102564 |
512820 / 4 = 128205 615384 / 4 = 153846 714285 / 5 = 142857 |
717948 / 4 = 179487 820512 / 4 = 205128 923076 / 4 = 230769 |
|
|
Création
de cycle Le procédé produit parfois un cycle. sur le reste. |
103448275862000… / 3 = 344827586206666,666… |
|||
|
Même procédé que précédemment, mais cette fois, c'est le chiffre de queue
qui passe en tête. |
157 894 736 842 105 263 / 2 = 3157 894 736 842 105 26 857142
/ 3 = 285714 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |