|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
Avec le carré: le nombre N à D chiffres est un nombre de Kaprekar si en partageant son carré en deux
nombres de D chiffres, la somme de ces deux nombres est égale à N. Généralisation à l'ordre k: si le nombre à la puissance k, partagé en k
nombres de D chiffres, leur somme est
égale à N.
Anglais: N is a Kaprekar number
if it has D digits, and if you take N2 and divide it into two
pieces each D digits in size and add them together, you get N. |
Voir Pépites
|
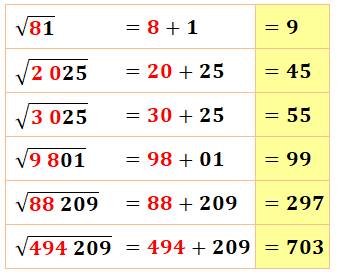
Racines carrés magiques Pour
ces nombres, la racine se calcule facilement:
Attention Cela
ne marche que pour les nombres de Kaprekar. |
|
||
|
Liste
des nombres de Kaprekar |
1,
81, 2025, 3025, 9801, 88209, 494209, 998001, 4941729, 7441984, 23804641, 24502500,
25502500, 28005264, 52881984, 60481729, 99980001, 300814336, 493817284,
1518037444, 6049417284, 6832014336, 9048004641, 9999800001, 20408122449,
21948126201, 33058148761, 35010152100, 43470165025, 101558217124,
108878221089, 123448227904, 127194229449, 152344237969, 213018248521,
217930248900, 249500250000, 250500250000, 284270248900, … |
||
|
Liste
des racines des nombres de Kaprekar |
1,
9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, 7272, 7777,
9999, 17344, 22222, 38962, 77778, 82656, 95121, 99999, 142857, 148149,
181819, 187110, 208495, 318682, 329967, 351352, 356643, 390313, 461539,
466830, 499500, 500500, 533170, … |
||
Voir Brève 59-1168
|
NOMBRES de KAPREKAR |
|
|
Nombre tel que son carré, dont on ajoute les parties, redonne le
nombre de départ. 297² = 88 209
& 088 + 209 = 297 Note: on ajoute des 0 à
gauche si nécessaire pour satisfaire la définition demandant D chiffres pour
chacun de nombres. Lorsqu'on élève au carré un nombre de Kaprekar à n chiffres et qu'on
ajoute les n chiffres de droite au n, ou n-1, de gauche, on retrouve le
nombre d'origine. Liste des nombres de
Kaprekar
Suite en Tables Les propriétés avec 999 … se
retrouvent avec 666 … et 333…
Curiosités avec repdigits
|
|
Voir Nombres
à motifs / Somme des
chiffres d'une puissance / Repdigits en 9
|
|
|
|
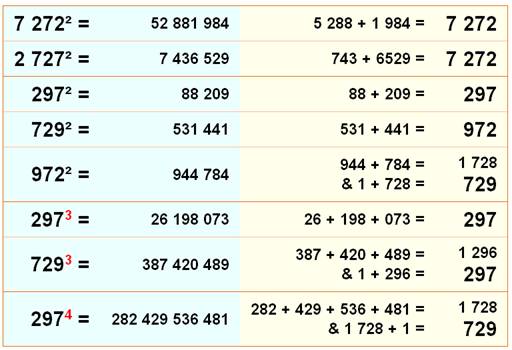
Repdigit en 9 Tous les repdigits en 9 sont des nombres de Kaprekar. 99² = 9801 & 98 + 1 = 99 999² = 99801 & 998 + 1 = 999 … 99…9² = 99…98 00…01 &
99...98 + 1 = 99…9 Permutations cycliques Si on élève au carré une permutation cyclique d'un nombre de Kaprekar et qu'on additionne les " moitiés ", on obtient
une permutation cyclique du nombre de départ. Avec les autres puissances le procédé de troncature fonctionne encore.
Avec la puissance n, il faut partager en n parts égales. Une addition
supplémentaire est parfois nécessaire lorsque le nombre final est trop grand.
|
|
SUPER-KAPREKAR: motifs Kaprekar
avec les puissances de 45 = 20 + 25

Voir Nombre 45 -
Kaprekar / Nombre 2025
|
|
|
|
The Kaprekar routine is an algorithm discovered in
1949 by D. R. Kaprekar for 4-digit numbers, but which can be generalized to
k-digit numbers. The Kaprekar numbers:
You may have to repeat
this procedure. The end result is always
6174, but there are no more than seven steps. A Kaprekar's famous
discoveries is the Kaprekar constant, or
6,174. Although this number may seem ordinary on the surface, it is actually
quite spectacular! Take any four digit number of your choice. Arrange the
digits in descending order and subtract the digits arranged in ascending
order. Keep doing this over and over and in no more than 7 tries, you will
have 6,174. |
|
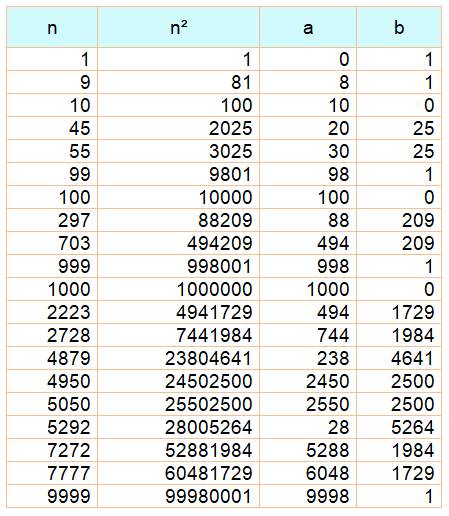
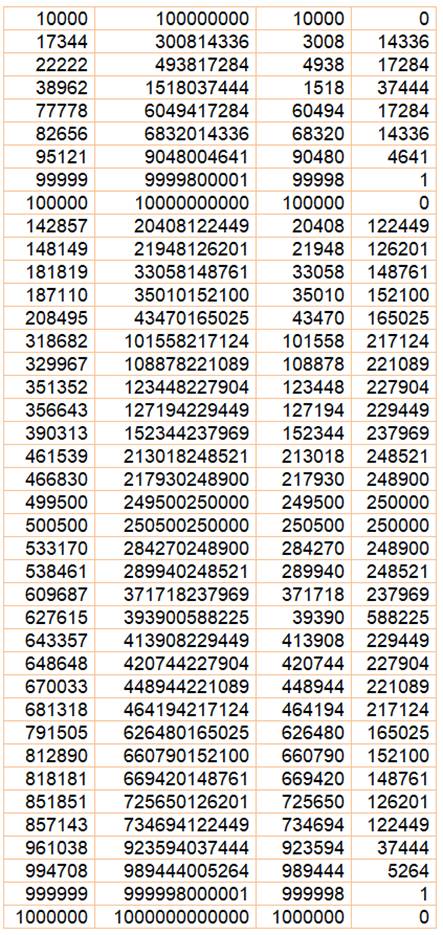
TABLE des nombres de Kaprekar généralisés avec des carrés
La césure n'est pas
forcément au milieu du nombre
Ex: 297² = 88 209 et 88
+ 209 = 297
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()