Itération: inverse chiffres et ajoute constante

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/11/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Suite de nombres
Débutants Général	Itérations – Cycles				Glossaire Suites et Séries
INDEX Itérations Rubriques	Algorithme de Kaprekar		RATS (Kaprekar avec tri)	RADD (inversion et somme)
	Racines numériques		Cycle des Carrés	Cycle de Syracuse
	Powertrain		De base en base	Autres – Index
		Sommaire de cette page >>> Approche avec RADD(1, 20) >>> S = RADD (n, k) >>> Exemples avec n = 1 puis n = 2 >>> RADD(1, k) – Trajectoires >>> Programmation

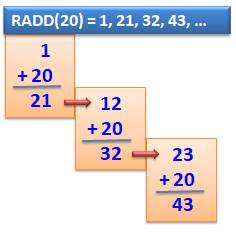
RADD (Reverse digits then ADD)

Retourne le nombre

et ajoute une constante

Le nombre de départ de la suite itérative: 1, par exemple;

Ajouter une constante: k = 20, par exemple;
Retourner le nombre: 21 devient 12; et

Poursuivre le procédé: 12 + 20 = 32 …

Approche avec RADD(1, 20)
Il existe de nombreux procédé itératifs comme celui de Kaprekar (suivant = précédent + son retourné). Avec le procédé RADD, le nombre est retourné et on lui ajoute une constante pour former le suivant		Radd(n+1) = Retourne(Radd(n)) + 1
Cas de k = 20 avec 1 comme valeur initiale	RADD(1, 20) pour les 75 premières valeurs 1, 21, 32, 43, 54, 65, 76, 87, 98, 109, 921, 149, 961, 189, 1001, 1021, 1221, 1241, 1441, 1461, 1661, 1681, 1881, 1901, 1111, 1131, 1331, 1351, 1551, 1571, 1771, 1791, 1991, 2011, 1122, 2231, 1342, 2451, 1562, 2671, 1782, 2891, 2002, 2022, 2222, 2242, 2442, 2462, 2662, 2682, 2882, 2902, 2112, 2132, 2332, 2352, 2552, 2572, 2772, 2792, 2992, 3012, 2123, 3232, 2343, 3452, 2563, 3672, 2783, 3892, 3003, 3023, 3223, 3243, 3443, 3463, 3663, 3683, 3883, 3903, 3113, 3133, 3333, 3353, 3553, 3573, 3773, 3793, 3993, 4013, 3124, 4233, 3344, 4453, 3564, 4673, 3784, 4893, 4004, 4024, 4224, …
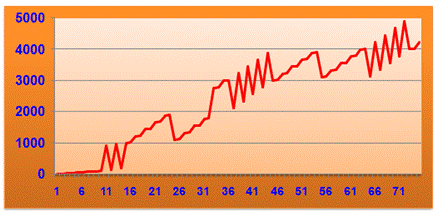
Trajectoire de la suite La suite semble irrémédiablement divergente En effet: Pour 1 000 : Radd = 93 882 Pour 10 000: Radd = 1 542 441

S = RADD (n, k)
La suite de nombres S est formée en partant de la valeur initiale n et en appliquant le procédé RADD: retournement du nombre et addition d'une constante k. Les zéros de têt dans un nombre sont ignorés (100 devient 1).		*Initialement proposé par Luc Stevens à J.A.Sloane, ce procédé itératif a été étudié par David Applegate, Klaus Brockhaus et autres.*
Trajectoires Elles sont de deux types:	Jamais de fin, ou Finissent par un cycle de longueur finie

Exemples avec n = 1 puis n = 2

RADD(1, 1)

Cycle de longueur 9 atteint à la première itération avec le nombre 2.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 3, 4,

Notation

RADD (1,1) = 2, 9, [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

RADD(1, 2)

Cycle de longueur 81 atteint à la première itération avec le nombre 3.

3, 81, [1, 3, 5, 7, 9, 11, 13, 33, 35, 55, 57, 77, 79, 99, 101, 103, 303, 305, 50 5, 507, 707, 709, 909, 911, 121, 123, 323, 325, 525, 527, 727, 729, 929, 931, 141, 143, 343, 345, 545, 547, 747, 749, 949, 951, 161, 163, 363, 365, 565, 567, 767, 769, 969, 971, 181, 183, 383, 385, 585, 587, 787, 789, 989, 991, 201, 104, 403, 306, 605, 508, 807, 710, 19, 93, 41, 16, 63, 38, 85, 60, 8, 10]

RADD(1, 3)

Cycle de longueur 3 atteint à la première itération avec le nombre 4.

4, 3, [1, 4, 7, 10]

RADD(1, 9)

Boucle sur 1 et 10

10, 2, [1, 10]

RADD(1, 10)

Cycle sans fin

929+, 101+, [1, 11, 21, 22, 32, 33, 43, 44, 54, 55, 65, 66, 76, 77, 87, 88, 98, 99, 109, 911, 129, 931, 149, 951, 169, 971, 189, 991, 209, 912, 229, 932, 249, 952, 269, 972, 289, 992, 309, 913, 329, 933, 349, 953, 369, 973, 389, 993, 409, 914, 429, 934, 449, 954, 469, 974, 489, 994, 509, 915, 529, 935, 549, 955, 569, 975, 589, 995, 609, 916, 629, 936, 649, 956, 669, 976, 689, 996, 709, 917, 729, 937, 749, 957, 769, 977, 789, 997, 809, 918, 829, 938, 849, 958, 869, 978, 889, 998, 909, 919, 929, …]

RADD(1, 11)

Cycle de longueur 9 atteint à la première itération avec le nombre 12.

12, 9, [1, 12, 32, 34, 54, 56, 76, 78, 98, 100]

RADD(1, 12)

Cycle de longueur 15 atteint à la deuxième itération avec le nombre 43.

43, 15, [1, 13, 43, 46, 76, 79, 109, 913, 331, 145, 553, 367, 775, 589, 997, 811, 130]

RADD(1, 13)

Cycle de longueur 18 atteint à la 31^e itération avec le nombre 80.

80, 18, [1, 14, 54, 58, 98, 102, 214, 425, 537, 748, 860, 81, 31, 26, 75, 70, 20, 15, 64, 59, 108, 814, 431, 147, 754, 470, 87, 91, 32, 36, 76, 80, 21, 25, 65, 69, 109, 914, 432, 247, 755, 570, 88, 101, 114, 424, 437, 747, 760]

RADD(2, 1)

Cycle de longueur 3 atteint à la deuxième itération avec le nombre 4.

2, 9, [2, 3, 4, 5, 6, 7, 8, 9, 10]

RADD(2, 2)

Cycle de longueur 80 atteint à la troisième itération avec le nombre 8.

8, 81, [2, 4, 6, 8, 10, 3, 5, 7, 9, 11, 13, 33, 35, 55, 57, 77, 79, 99, 101, 103, 303, 305, 505, 507, 707, 709, 909, 911, 121, 123, 323, 325, 525, 527, 727, 729, 929, 931, 141, 143, 343, 345, 545, 547, 747, 749, 949, 951, 161, 163, 363, 365, 565, 567, 767, 769, 969, 971, 181, 183, 383, 385, 585, 587, 787, 789, 989, 991, 201, 104, 403, 306, 605, 508, 807, 710, 19, 93, 41, 16, 63, 38, 85, 60]

RADD(1, k) – Trajectoires

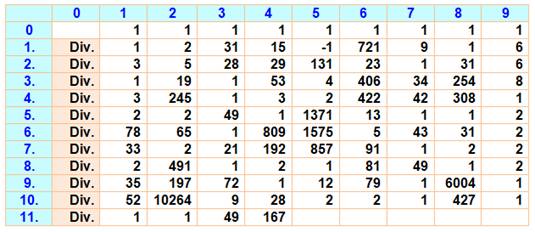
Ce tableau pour k de 1 à 114 indique la quantité d'itérations pour le départ d'un cycle avec Radd(1, k).

Les k divisible par 10 conduisent à une suite sans fin.

Ex: Radd(1, 13), le cycle commence à la 31^e itération.

Programmation

Programme Maple

But

Créer la suite des nombres RADD(n,k) en identifiant les cycles.

Commentaires

On utilise la procédure d'inversion d'un nombre. L'instruction irem retourne le reste de la division.

Le programme principal est initialisé avec les valeurs de n et k et prépare la liste L à éditer, de même que l'ensemble S des nombres qui vont être trouvés au fur et à mesure de la recherche.

Procédé RADD pour calculer la nouvelle valeur de n. Si le nouveau nombre est dans la liste S, arrêt et impression de n, de la taille de la liste et de la liste.

Ici, RADD(3, 3) s'arrête au nombre 12. On compte six itérations pour le cycle. En effet: 90 donne 9 + 3 = 12.

Si le deuxième chiffre est 101, c'est que le cycle dépasse 100 ou est infini.

L'instruction en bas peut être ajoutée en fin de programme pour identifier le rang du départ de cycle.

Voir Programmation – Index

Suite	Autres séquences de ce type Nombres narcissiques Retournés et premiers Cycle de Syracuse Autres en haut de page
Voir	Boucle infernale Calcul mental Division qui retourne le nombre Géométrie Nombre Harshad Nombres retournés Palindrome retard Preuve par neuf en pratique Récurrence Théorie des nombres
Sites	Sequences of RADD type – OEIS – Références pour atteindre toutes ces sortes de suites OEIS A117816 – Number of steps until the RADD sequence T(k+1) = n + R(T(k)), T(0) = 1 Reverse and Add Function – GeeksforGeeks – Programmation en Python et autres de la fonction inverse et ajoute; peut donner des idées pour programmer la fonction RADD.
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/RADD.htm