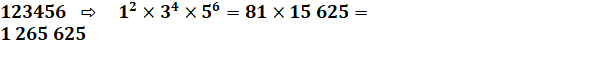Powertrain: un chiffre sur deux en puissance

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/02/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Suite de nombres
Débutants Général	Itérations – Cycles				Glossaire Suites et Séries
INDEX Itérations Rubriques	Suite de Fibonacci		Triangle de Pascal	Triangle de Leibniz
	Algorithme de Kaprekar		Cycle de Syracuse	Cycle des Carrés
	Nombres de Kaprekar		Cycle de Syracuse Géné.	Suite de Padovan
	Cycle-cube et 153		Nombres Chanceux	Suite de Steinhaus
	Cycle de Keith		Racines numériques	Somme x Produit
	Powertrain		De base en base	Suite Q d'Hofstadter
	Nombres de Gilda		Premier Maison
		Sommaire de cette page >>> Transformation powertrain >>> Liste des valeurs du powertrain >>> Racine powertrain >>> Nombres sans racine powertrain >>> Racine powertrain = 4

POWERTRAIN

Produit des chiffres avec puissances

Création d'un nouveau nombre à partir des chiffres d'un nombre: c'est le produit de chaque chiffre de rang impair élevé à la puissance du chiffre de rang pair.

Transformation powertrain

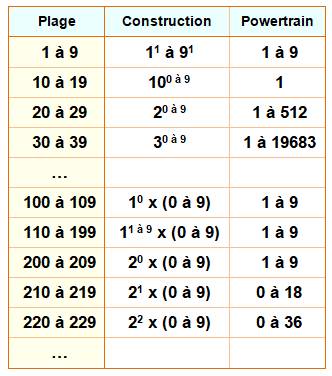
La transformation powertrain consiste à multiplier les couples des chiffres, le second étant un exposant.
1234567 devient 1²·3⁴·5⁶·7

La transformation powertrain des premiers nombres est particulièrement simple.

Les nombres qui commencent par 1, par exemple, contribuent pour un facteur 1, quel que soit le deuxième chiffre.

Table des powertrain

Liste des valeurs du powertrain

Pour n de 0 à 499

Ex: 499 donne
4⁹ x 9
= 262 144 x 9
= 2359296

0, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 1, 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1, 5, 25, 125, 625, 3125, 15625, 78125, 390625, 1953125, 1, 6, 36, 216, 1296, 7776, 46656, 279936, 1679616, 10077696, 1, 7, 49, 343, 2401, 16807, 117649, 823543, 5764801, 40353607, 1, 8, 64, 512, 4096, 32768, 262144, 2097152, 16777216, 134217728, 1, 9, 81, 729, 6561, 59049, 531441, 4782969, 43046721, 387420489]

100, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

200, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 0, 16, 32, 48, 64, 80, 96, 112, 128, 144, 0, 32, 64, 96, 128, 160, 192, 224, 256, 288, 0, 64, 128, 192, 256, 320, 384, 448, 512, 576, 0, 128, 256, 384, 512, 640, 768, 896, 1024, 1152, 0, 256, 512, 768, 1024, 1280, 1536, 1792, 2048, 2304, 0, 512, 1024, 1536, 2048, 2560, 3072, 3584, 4096, 4608]

300, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 0, 9, 18, 27, 36, 45, 54, 63, 72, 81, 0, 27, 54, 81, 108, 135, 162, 189, 216, 243, 0, 81, 162, 243, 324, 405, 486, 567, 648, 729, 0, 243, 486, 729, 972, 1215, 1458, 1701, 1944, 2187, 0, 729, 1458, 2187, 2916, 3645, 4374, 5103, 5832, 6561, 0, 2187, 4374, 6561, 8748, 10935, 13122, 15309, 17496, 19683, 0, 6561, 13122, 19683, 26244, 32805, 39366, 45927, 52488, 59049, 0, 19683, 39366, 59049, 78732, 98415, 118098, 137781, 157464, 177147]

400, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 0, 16, 32, 48, 64, 80, 96, 112, 128, 144, 0, 64, 128, 192, 256, 320, 384, 448, 512, 576, 0, 256, 512, 768, 1024, 1280, 1536, 1792, 2048, 2304, 0, 1024, 2048, 3072, 4096, 5120, 6144, 7168, 8192, 9216, 0, 4096, 8192, 12288, 16384, 20480, 24576, 28672, 32768, 36864, 0, 16384, 32768, 49152, 65536, 81920, 98304, 114688, 131072, 147456, 0, 65536, 131072, 196608, 262144, 327680, 393216, 458752, 524288, 589824, 0, 262144, 524288, 786432, 1048576, 1310720, 1572864, 1835008, 2097152, 2359296]

Racine powertrain
L'idée consiste à appliquer le procédé powertrain de manière itérative jusqu'à aboutir à un nombre à un seul chiffre. Avec l'exemple du nombre 55, la racine powertrain est 0, obtenue en cinq itérations. Voir Brève 802	Exemple 55, 5, [3125, 96, 531441, 500, 0]
Tous les nombres jusqu'à 23 se terminent en une seule itération: 17 => 1⁷ = 1.	Le plus petit nombre à deux itérations est 24: 2⁴ = 16 et 1⁶ = 1.
Liste des nombres de 1 à 100 avec calcul de la racine en plus de une étape 24, 2, [16, 1] 25, 2, [32, 9] 26, 5, [64, 1296, 531441, 500, 0] 27, 2, [128, 8] 28, 3, [256, 192, 2] 29, 3, [512, 10, 1] 33, 3, [27, 128, 8] 34, 2, [81, 8] 35, 5, [243, 48, 65536, 5832000, 0] 36, 5, [729, 441, 256, 192, 2] 37, 5, [2187, 4194304, 104976, 30840979456, 0] 38, 4, [6561, 46656, 191102976, 0] 39, 9, [19683, 5038848, 214990848, 17179869184, 1735247072139264, 19999187712, 102372436321763328, 8813365017182208, 0] 42, 2, [16, 1] 43, 5, [64, 1296, 531441, 500, 0] 44, 3, [256, 192, 2] 45, 3, [1024, 16, 1] 46, 4, [4096, 531441, 500, 0] 47, 6, [16384, 26244, 4096, 531441, 500, 0] 48, 3, [65536, 5832000, 0] 49, 5, [262144, 32768, 8470728, 1605632, 0] 52, 3, [25, 32, 9] 53, 2, [125, 5] 54, 3, [625, 180, 0] 55, 5, [3125, 96, 531441, 500, 0] 56, 3, [15625, 180, 0] 57, 3, [78125, 28824005, 0] 58, 2, [390625, 0] 59, 4, [1953125, 625, 180, 0] 62, 6, [36, 729, 441, 256, 192, 2] 63, 3, [216, 12, 1] 64, 4, [1296, 531441, 500, 0] 65, 4, [7776, 96889010407, 62412703137792, 0] 66, 3, [46656, 191102976, 0] 67, 3, [279936, 36150980669568, 0] 68, 8, [1679616, 1452729852, 1318305830625, 70312500, 96, 531441, 500, 0] 69, 2, [10077696, 0] 72, 6, [49, 262144, 32768, 8470728, 1605632, 0] 73, 6, [343, 243, 48, 65536, 5832000, 0] 74, 2, [2401, 0] 75, 2, [16807, 7] 76, 3, [117649, 30840979456, 0] 77, 5, [823543, 995328, 12397455648000, 191398476150000, 0] 78, 3, [5764801, 101250000, 0] 79, 2, [40353607, 0] 82, 5, [64, 1296, 531441, 500, 0] 83, 3, [512, 10, 1] 84, 4, [4096, 531441, 500, 0] 85, 4, [32768, 8470728, 1605632, 0] 86, 5, [262144, 32768, 8470728, 1605632, 0] 87, 4, [2097152, 9565938, 2677850419968, 0] 88, 3, [16777216, 40353607, 0] 89, 7, [134217728, 6272, 1764, 1296, 531441, 500, 0] 92, 2, [81, 8] 93, 5, [729, 441, 256, 192, 2] 94, 4, [6561, 46656, 191102976, 0] 95, 2, [59049, 0] 96, 3, [531441, 500, 0] 97, 3, [4782969, 5015306502144, 0] 98, 2, [43046721, 0] 99, 4, [387420489, 9291474468864, 5385144351531158470656, 0]

Nombres SANS racine powertrain

Nombre auto racine powertrain

Le seul nombre égal à son powertrain (au moins jusqu'à 1 000 000). Ce nombre est aussi appelé "faute de frappe".

Le nombre 642 qui produit 2 592 a un processus itératif sans fin, donc aucune racine à un chiffre. C'est le plus petit.

La suite des nombres qui ont une racine égale à 2592 figure à droite. Ils n'ont pas de racine à un chiffre.

Nombres sans racine powertrain

642, 2164, 2534, 2592, 3425, 6421, 9225, 10642, 11642, 12642, 13642, 14642, 15642, 16642, 17642, 18642, 19642, 20642, 21636, 21641, 22348, 22633, 22928, 23344, 23629, 23924, 24336, 24342, 24922, 25329, 25333, 25341, 25919, 25921, 30642, 31634, 32259, 32628, 33246, 33253, 33426, 34228, 34234, 34242, 34251, 34418, 34422, 34814, 40642, 41348, 41633, 41928, 42336, 42342, 42922, 50642, 60642, 61632, 62239, 62328, 62622, 62819, 62918, 63216, 63223, 63314, 63413, 63612, 64002, 64102, 64112, 64122, 64132, 64142, 64152, 64162, 64172, 64182, 64192, 64202, 64211, 64302, 64402, 64502, 64602, 64702, 64802, 64902, 70642, 80642, 81344, 81629, 81924, 90642, 91259, 91628, 92228, 92234, 92242, 92251, 92418, 92422, 92814, …

Voir Nombres faute de frappe pour d'autres nombres de ce type

Racine powertain = 4

Tous: 114 cas jusqu'à 10 000

4, 22, 41, 104, 114, 124, 134, 144, 154, 164, 174, 184, 194, 204, 212, 221, 249, 304, 404, 411, 429, 504, 604, 624, 704, 804, 904, 1022, 1041, 1122, 1141, 1222, 1241, 1322, 1341, 1422, 1441, 1522, 1541, 1622, 1641, 1722, 1741, 1822, 1841, 1922, 1941, 2022, 2041, 2121, 2200, 2210, 2211, 2212, 2213, 2214, 2215, 2216, 2217, 2218, 2219, 2220, 2230, 2240, 2250, 2260, 2262, 2270, 2280, 2290, 2432, 2491, 3022, 3041, 3224, 3242, 4022, 4041, 4100, 4110, 4111, 4112, 4113, 4114, 4115, 4116, 4117, 4118, 4119, 4120, 4130, 4140, 4150, 4160, 4162, 4170, 4180, 4190, 4232, 4291, 5022, 5041, 6022, 6041, 6222, 6241, 7022, 7041, 8022, 8041, 9022, 9041, 9124, 9142.

Racine en deux itérations jusqu'à 10 000

249, 429, 624, 2262, 2432, 2491, 3224, 3242, 4162, 4232, 4291, 6222, 6241, 9124, 9142.

Avec plus de deux itérations jusqu'à 100 000

37494, 37556, 37864, 38552, 38578, 45678, 46672, 47663, 49374, 55376, 55382, 55942, 57388, 57948, 63728, 65859, 66473, 67458, 67462, 67842, 72638, 84672, 85659, 86374, 94552, 94578

Record du nombre d'itérations jusqu'à 60 000 000

4, 1, [4]
249,2, [144, 4]

37 494, 3, [2293235712, 1822500000, 4]

63 728, 4, [84672, 2293235712, 1822500000, 4]

Suite	Autres séquences de ce type Nombres narcissiques Retournés et premiers Cycle de Syracuse Autres en haut de page
Voir	Boucle infernale Calcul mental Division qui retourne le nombre Géométrie Nombre Harshad Nombres retournés Palindrome retard Preuve par neuf en pratique Récurrence Théorie des nombres
Sites	OEIS A133500 – The powertrain or power train map OEIS A326737 – Numbers which converge to 4 under repeated application of the powertrain map
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Powertra.htm