|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres HARSHADS ou nombres de NIVEN ou nombres multinumériques Propriété
des nombres face à la somme
de ses chiffres. |

Harshad et Niven
|
Harshad Harshad = grande joie, en sanskrit (harṣa: joie et da: donner). Nom
donné par le mathématicien indien Kaprekar. On
doit donc écrire: nombres harshads
(adjectif, avec minuscule et marque du pluriel) – Merci à M.Hasler pour
cette remarque pertinente. Niven Lors
d'une conférence en 1977, Ivan Niven présente des nombres qui sont divisibles
par 2 fois la somme de leurs chiffres. En
1982, en son honneur, Kennedy baptise les nombres divisibles par la somme de
leurs chiffres nombres de Niven. |
|
|
|
|
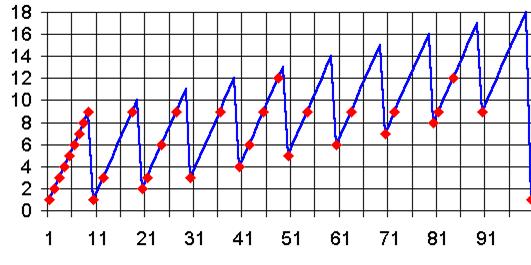
Qu'est-ce qu'un nombre
harshad Analysons la division des 100 premiers
nombres (N) par la somme des chiffres de chaque nombre (SC) Exemple N = 12 SC = 1 + 2 = 3 N / SC = 12 / 3 = 4 Lorsque la division tombe juste, comme ici:
N est un nombre harshad. Illustration En bleu : la courbe donnant N
/ SC en fonction de N En rouge : les nombres
harshads
|
|
Voir Nombres k fois la somme de ses chiffres
/ Nombres somme ou produit des chiffres
|
|
||
|
Définition |
Nombre
qui est divisible par la somme de ses chiffres. |
|
|
Exemple |
10
/ 1 = 10, 12 / 3 = 4, 18 / 9 = 2, 20 /
2 = 10, 21 /3 = 7, 24 / 6 = 4 … |
|
|
Liste |
1, 2, 3,
4, 5, 6, 7, 8, 9, 10, 12, 18, 20, 21, 24, 27,
30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70, 72, 80, 81, 84, 90, 100, 102,
108, 110, 111, 112, 114, 117, 120, 126, 132,
133, 135, 140, 144, 150, 152, 153, 156, 162, 171, 180, 190, 192, 195, 198,
200 … |
|
|
Chaine de harshads |
510,
511, 512, 513 1014,
1015, 1016, 1017 2022,
2023, 2024, 2025 3030,
3031, 3032, 3033 Chaines de
quatre: 510, 1014,
2022, 3030, 10 307, 12 102, 12 255, 13 110, 60 398, 31 215, 93 040, … Première chaîne de cinq
harshad consécutifs: 131
052, 131 053, 131 054, 131 055, 131 056 Suivante:
491 424 … Bilan La
première chaine de k nombres harshads consécutifs se rencontre pour: H2
= 20; H3 = 110; H4 = 510; H5 = 131 052; H6
= H7 = 10 000 095; H8 = H9 = 124 324 220 |
|
|
Trous harshads |
17
nombres consécutifs non harshads: 558
– 576, 666 – 684, 736 – 756, 846 – 864, 972 – 990 |
|
|
Années harshads |
1998,
2000, 2001, 2004, 2007, 2010, 2016, 2020, 2022, 2023, 2024… |
|
|
Harshad complet |
Nombre
qui est harshad dans toutes les bases. Ils ne sont que quatre. 1, 2, 4 et
6. Anglais: all-harshad |
|
|
Propriétés |
Il n'existe pas de séquence de plus de 20 nombres
harshads consécutifs. Grundman (1994)
La plus petite séquence de 20 nombres consécutifs contient
des nombres à 44 363 342 786 chiffres. Tous les nombres premiers supérieurs à 10 ne sont
pas harshads. Toutes factorielles jusqu'à 431! sont nombres
harshads. 432! ne l'est pas. |
|
|
Integer sequence |
Niven(or harshad) numbers:
numbers: numbers that are divisible by the sum of their digits. (Cette présente page y est citée) |
|
|
Recherche |
|
||
|
Nombre |
Exemple |
Règle |
|
|
101 : non |
Nombre
impair somme
paire. |
Aucun
nombre impair n'est divisible par un pair. |
|
|
109 : non |
Somme
10 |
N'est
divisible par 10 que si terminé par 0. |
|
|
104 : non |
Somme
5 |
N'est
divisible par 5 que si terminé par 0 ou par 5. |
|
|
Attention |
Les
critères de divisibilité doivent être appliqués
avec précaution! |
||
|
108: oui |
Somme
9 |
Divisible
par 9. Attention somme 9 rigoureusement et non pas la racine
numérique de la preuve
par 9. |
|
|
111: oui |
Somme
3 |
Divisible
par 3. Même remarque. |
|
|
112: oui |
Somme
4 |
et
12 divisible par 4. Même type de remarque. |
|
Voir Démonstration
que 108 = 12 (1+0+8) est le seul
divisible 12
|
|
|||
|
Deux méthode pour obtenir
les chiffres |
|
||
|
-------------------------------------------------------------
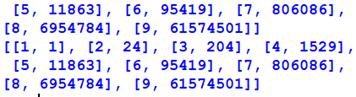
[8, 6 954 784] temps
calcul: environ 2 minutes. [9, 61 574 519] temps
supérieur à la demi-heure. Voir liste
ci-dessous |
Programme Python
– Commentaires Définition de la fonction de recherche des nombres harshads. Somme des chiffres de n (Sch)
initialisée à 0. Le nombre n va être itérativement tronqué de ses unités (nn). Tant que ce nombre tronqué reste positif, on ajoute l'unité à la somme
des chiffres. L'unité est donnée par nn mod
10 (nn % 10) . Le nombre nn suivant est le quotient (//)
de nn courant. Le programme courant constitue une liste des nombres harshads dans L. Le programme suivant établit la liste (S)
de la quantité de harshads pour les nombres jusqu'à 10k . Si n est un harshad on incrément le compteur kt. Si n est en 10k , on ajoute (append) la paire k et kt à la
liste S en cours. Impression ce cette liste en fin de programme. Ainsi, il y a 95 419 nombres harshads jusqu'à 1 000 000, sans compter
les 10 premiers nombres (0 à 9). Quantité de harshads de:
|
||
Quantité de nombres harshads
|
Selon
la puissance de 10k et à partir de 1 (et 103a en rose)
: 10,
33, 213, 1 538,
11 872, 95 428,
806 095, 6 954 793, 61 574 510, 553 007 106,
5 024 332 415, 45 975 917 532,
422 675 487 735, 3 902 487 368 735, 36 116 199 480
944, 335 270 244 411 437, 3 128 167 760 734 131, 29 410 615 796
612 778, 278 977 554 117 741
592, 2 664 295 247 105 153 610, 25 539 536 718
894 979 516, … |
Source: OEIS – De Koninck
|
|
Programme Maple
– Commentaires Boucle de recherche pour n de 10 à 30. La conversion en base 10 de n donne la liste des chiffres de n dans N.
La quantité de chiffres (nops) est mémorisée en q. S est l'addition des chiffres de n de rang 1 à q, chacun étant extrait
par N[i]. Q est le quotient de n par la somme de ses chiffres (définition du
nombre harshad). Si le quotient est un entier (integer), n est déclaré nombre harshad
et il est imprimé avec la valeur S, de la somme des chiffres et Q, la valeur
du quotient. L'affichage donne les huit nombres harshads compris entre 10 et 30. |
|
|
|||||||||||||||||||||||||
|
Somme d'un nombre harshad qui termine aussi ce nombre
harshad. Sandro Boscaro Exemples: avec les plus petits harshads (rien avant 910 sinon les unités) Les harshads morphiques sont notés en rouge.
Sans surprise, les suivants
sont: 2710, 2712, 2715, 2718, 3610 … 4510 … 5410 …6310… 7210 …811 …9010 … 9920 Propriété Il n'y a pas de nombre harshad morphique terminé par 11
(sauf 11). Premiers nombres
harshads morphiques Hm Hm jusqu'à 66 pour les harshads jusqu'à 108
|
|||||||||||||||||||||||||
Anglais: Harshad or Niven morphic numbers
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()