Triangles à même aire

Édition du: 24/10/2022

INDEX Triangle Géométrie	Triangles entiers
	Triangles	Entiers	Pythagore	Même aire
	Isiaque	Héron	Congruents	Entier équilatéral
		Fibonaci

Triangles ENTIERS

Même aire et
une dimension commune

Quels sont les triangles dont la longueur des côtés est un nombre entier.

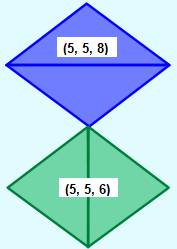
Propriétés avec l'aire et le périmètre, eux aussi des nombres entiers.

La figure montre deux triangles isocèles de même aire (12) et dont les longueurs des côtés sont des entiers. Les deux paires de côtés égaux de chaque triangle isocèle sont de même longueur (5).

Sommaire de cette page

>>> Triangles quelconques

>>> Triangles isocèles

>>> Triangles rectangles

Débutants

Triangle

Glossaire

Triangle

Triangles quelconques		haut
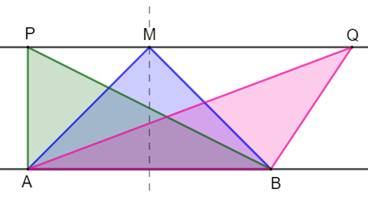
Propriété des triangles Tous les triangles ayant une côté commun et le sommet opposé situé sur une parallèle au côté commun ont la même aire. Cela du fait que l'aire est le demi-produit de la base par la hauteur.	Tous ces triangles ayant la même hauteur et un côté commun ont une aire identique.
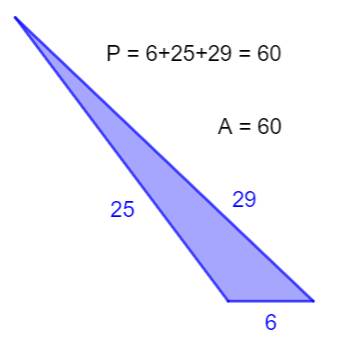
Triangles héroniens Deux triangles héroniens (côtés et aire sont des nombres entiers) répondent à la condition s'ils ont la même aire. Le tableau de la page consacrée à ces triangles donne les solutions. Exemples Il existe quatre triangles héroniens d'aire 60: Deux triangles isocèles: 13, 13, 60 et 13, 13, 10 Un triangle rectangle: 8, 15, 17 Un triangle quelconque: 6, 25, 29	Exemples pour aire = 60
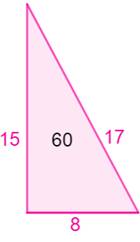
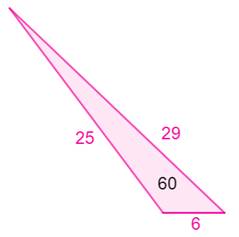
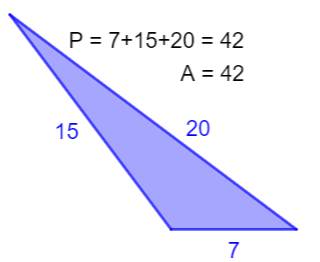
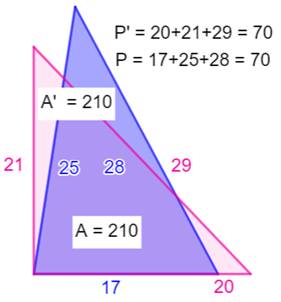
Aires et périmètres identiques Seuls cinq triangles à côtés entiers ont la même valeur pour le périmètre et l'aire: (6, 8, 10), (5, 12, 13), (6, 25, 29), (7, 15, 20) et (9, 10, 17).

Voir Triangles quelconques

Triangles isocèles		haut
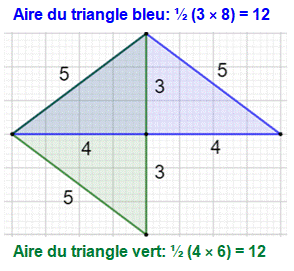
Avec le triangle (3, 4, 5) En assemblant trois de ces triangles comme sur la figure, on forme deux grands triangles isocèles: le bleu dont les dimensions sont: (5, 5, 8) et son aire est 12. le vert dont les dimensions sont: (5, 5, 6) et son aire est 12. Avec ce triplet de Pythagore (3² + 4² = 5²), on a formé deux triangles héroniens de même aire. Note: le triangle (5, 5, 8) est un triangle héronien de Fibonacci	Deux triangles de même aire Voir Triangles entiers
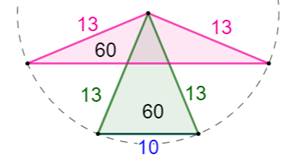
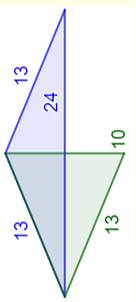
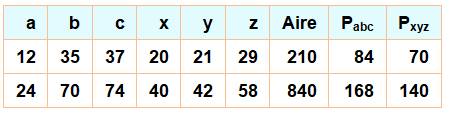
Généralisation à tout triplet *Le triplet qui suit (3, 4, 5) est (5, 12, 13). On peut créer deux triangles isocèles héroniens de même aire (figure):* le bleu dont les dimensions sont: (13, 13, 24) et son aire est 60. le vert dont les dimensions sont: (13, 13, 10) et son aire est 60. La table de droite montre les possibilités jusqu'à 50. Voir Triplets jumeaux pour table et formule des triplets suivants
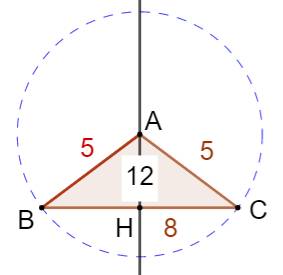
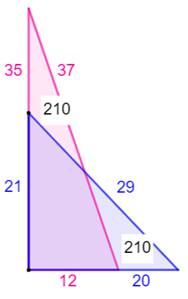
Construction Avec GeoGebra, il est possible de dessiner tous les triangles isocèles avec sa paire de côté de longueur constante. Il est alors possible d'observer l'évolution de la longueur de la base et celle de l'aire du triangle ABC. Point A; cercle (A, longueur des côtés, ici 5) Point B sur le cercle. Perpendiculaire en B à l'axe vertical. Intersection C Afficher les longueurs et l'aire

Triangles rectangles de mêmes aires		haut
Critère Deux triangles rectangles (a, b, c) et (x, y, z) ont la même aire si ab = xy Il faut donc trouver deus triplets de Pythagore ayant cette égalité de produit Exemple (Figure) Triangle (20, 21, 29): 20² + 21² = 29² = 841 et 20 x 21 = 420 Triangle (12, 35, 37): 12² + 35² = 37² = 1369 et 12 x 35 = 420
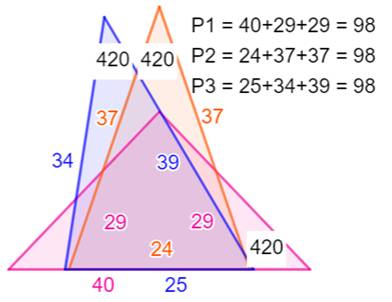
Listes des triangles rectangles de même aire: deux duos Même aire et même périmètre: un duo et un trio

Haut de page

Retour	*Voir* Haut de page
Suite	Triangles rectangles entiers – de Pythagore Triangles rectangles particuliers Triangle équilatéral
Voir	Losange Puzzle chinois Rectangle Triangle – Index Types de triangles
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TriaEgau.htm