|
||||||||||||||||||||||||||||||||||||
![]()
|
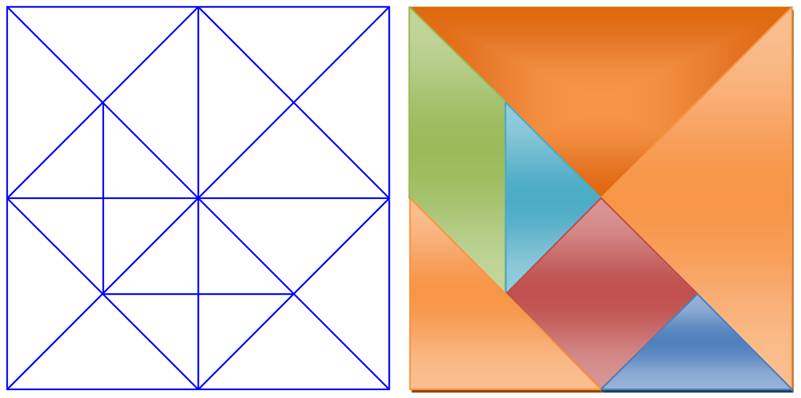
TANGRAM Dissection particulière du carré dont la disposition des pièces donne
lieu à des défis. Quelle est la géométrie de ce jeu? Quelles sont les autres possibilités
de dissections? Puzzle géométrique popularisé par Sam Loyd (1841-1911) dans son livre:
Le huitième livre de Tan (The Eight Book of Tan) publié en 1903. |
|
|
|
|
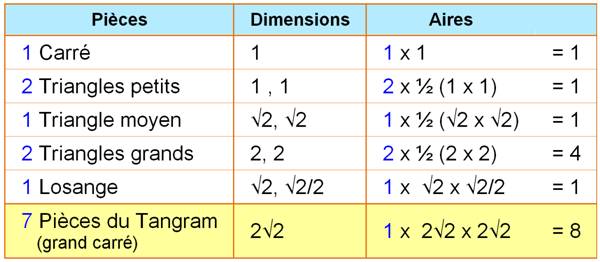
Les sept pièces |
|
|
|
|
|
|
|
|
|
|
|
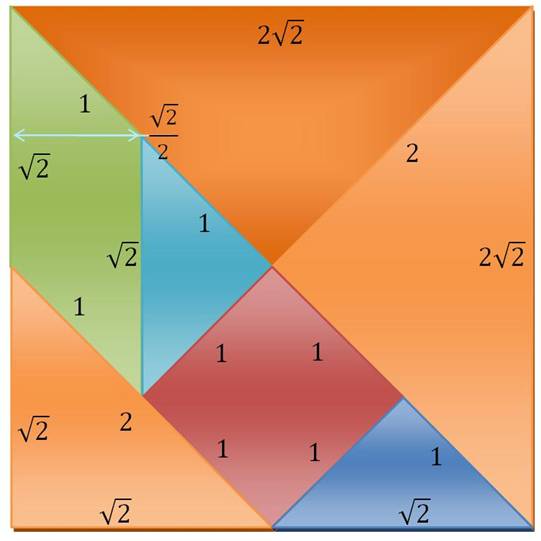
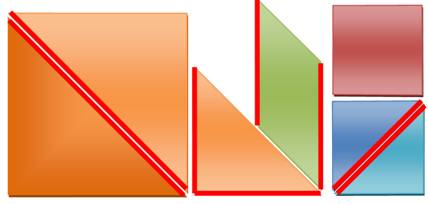
Carré:
c = 2 Rectangle:
L = 4 et l = 2.
Triangle:
4 Dans
les trois cas l'aire est égale à 8: Carré: (2 Rectangle: 4 x 2 ; Triangle: ½ x 2 |
|
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()