|
Édition du: 26/12/2024 |
|
INDEX |
GRAPHES, ARBRES & RÉSEAUX |
||
|
Graphes
– Index et vocabulaire |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
GRAPHES Index et vocabulaire
Liste des pages relatives aux graphes, aux arbres et aux réseaux.
Puis petit lexique des graphes.
|
||
|
|
Sommaire de cette page >>>
Rubriques – Graphes, arbres & réseaux >>>
Index graphes >>>
Vocabulaire des graphes |
Débutants Glossaire |
Anglais : Graph
Rubriques – GRAPHES, ARBRES &
RÉSEAUX
Anglais:
Graphs, trees and lattice paths
|
Graphes – Applications |
|||
|
Arbres |
|
|
|
INDEX VOISINS: Arbre / Graphe / Topologie / Dénombrement / Logique / Géométrie / Jeux et énigmes
|
Sommets
ou nœuds |
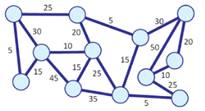
Ce genre de graphe est dit réseaux de points (sommets). |
|
|
Distance
entre deux sommets |
Longueur de la plus courte chaine qui relie ces deux sommets. |
|
|
Ordre
du graphe |
Quantité de sommets dans ce graphe. |
|
|
Diamètre
du graphe |
La plus grande des distances entre les paires de sommets du graphe. |
|
|
Rayon
du graphe |
La plus petite des distances entre les paires de sommets du graphe. |
|
|
Degré
d'un sommet |
Quantité d'arêtes présentes à ce sommet. >>> |
|
|
Arêtes
ou arcs |
Segment linéaire ou courbe joignant les sommets. Arc est plutôt utilisé lorsque l'arête est orientée. |
|
|
Adjacent
(sommets) |
Deux sommets sont adjacents s'ils sont reliés par une arête. |
|
|
Face
d'un graphe |
Chacune des régions délimitées par les arêtes, y compris la région
extérieure. Région délimitée par un chemin passant par trois sommets et ne
contenant aucun autre sommet. |
|
|
Graphe
connexe |
Graphe tels que toute paire de sommet peut être reliée par une chaine
(une suite d'arêtes). Ce graphe possède au moins n – 1 arêtes. |
|
|
Clique |
Sous-ensemble des sommets d'un graphe dont le sous-graphe induit est complet,
c'est-à-dire que deux sommets quelconques de la clique sont toujours
adjacents. |
|
|
Diagramme
sagittal |
Graphe qui représente les relations entre deux ensembles finis. Il
permet notamment de visualiser si une application est injective,
surjective ou bijective. |
|
|
Arbre |
Graphe qui ne contient aucun cycle (boucle). Ils sont donc planaires |
|
|
Graphe
complet |
Tous les sommets sont adjacents. Alors, chaque sommet est relié à tous
les autres. |
|
|
Graphe
de Grinder |
Voir exemples >>> |
|
|
Graphe
k-facteur |
Chaque sommet ne reçoit que k arêtes. |
|
|
K5 |
Graphe
complet à 5 sommets. Il n'est pas planaire. |
|
|
Graphe
biparti ou cyclique |
Les sommets sont divisés en deux groupes. Les sommets de l'un sont
reliés aux sommets de l'autre. |
|
|
K3,3 |
Graphe complet biparti de 3
+ 3 sommets. Il n'est pas planaire |
|
|
Graphe
planaire |
Un graphe planaire est
dessiné sur une feuille de papier, dans un plan, sans que les arêtes se
croisent. |
|
|
Nombre
chromatique |
Quantité maximale de couleurs pour colorier un graphe. >>> |
|
|
Graphe
planaire topologique |
Le graphe est dessiné dans une version qui montre que les arêtes ne se
croisent pas. Cette version du graphe est aussi appelée la carte du graphe
planaire. |
|
|
Graphe
planaire connexe |
Graphe qui n'a pas de sommets ou de sous-graphes isolés. Il existe toujours
un chemin pour relier deux sommets. |
|
|
Chemin
eulérien Chaine
eulérienne |
Le tracé en un seul trait est appelé chemin eulérien. La chaine contient toutes les arêtes et chaque arête n'est décrite
qu'une seule fois. |
|
|
Cycle
eulérien |
Chaine eulérienne fermée: le sommet de départ et celui d'arrivée sont
les mêmes. |
|
|
Graphe
eulérien |
Graphe que l'on peut dessiner sans jamais lever le crayon et sans
passer deux fois par la même arête. Un graphe est eulérien si et seulement si il contient une chaine
eulérienne ou un cycle eulérien. |
|
|
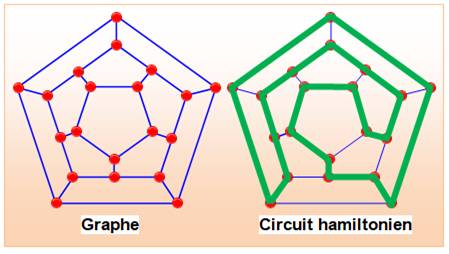
Chemin
hamiltonien |
Un tracé qui passe par tous les sommets (sans
forcément parcourir toutes les arêtes du graphe). Un graphe
hamiltonien est un graphe possédant au moins un cycle passant par tous les
sommets une fois et une seule. Un tel cycle élémentaire est alors appelé
cycle hamiltonien.
Exemples avec le problème de la table
ronde de Dudeney. Cycle hamiltonien dans le contexte du pavage d'Ammann-Beenker |
|
|
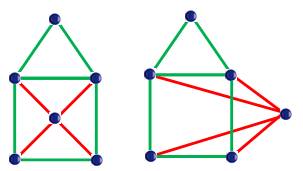
Graphes
isomorphes |
Graphes de mêmes caractéristiques: le degré des sommets est conservé.
La longueur des arcs et leur courbure n'influent pas sur les caractéristiques
du graphe. Exemple
Leur résolution en temps polynomial
est un problème ouvert. Voir Graphes
isomorphes |
|
Suite en Caractérisation des graphes
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/GrapheIX.htm
|