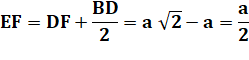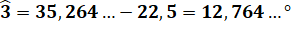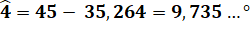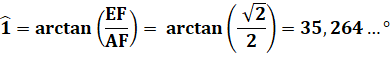|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Carré – Dissections Quelques exemples typiques de dissection du carré
puis le fameux exemple de trisection du carré par un mathématicien arabe de
la fin du premier millénaire, et tous les calculs associés. |
|
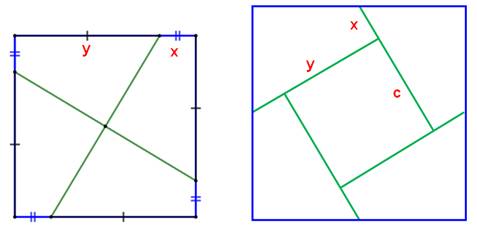
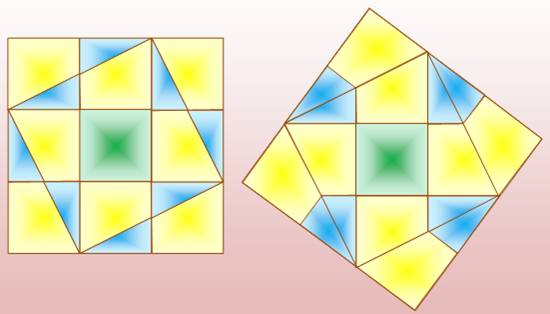
Construction Un carré est découpé en
quatre quadrilatères par deux sécantes (vertes) découpant chacun des segments
de longueur x et y sur les côtés. Ces quadrilatères sont
réassemblés en un carré formant un petit carré interne. Quelles sont les tailles de
ces deux carrés? Notez que Sur la figure de gauche, les
points d'intersection des sécantes est le centre du carré. Aussi, sur la figure de
droite les points d'intersection avec les côtés sont les milieux de ces
côtés. |
Figure initiale
|
|
|
Solution En portant les dimensions
sur les côtés des quadrilatères, il est facile de donner la taille du petit
carré: Pour le grand carré, son
côté a même longueur que chacun des deux segments obliques (verts) Un simple calcul avec le
théorème de Pythagore donne: |
Figure avec notations avec x = 2
|
|
Voir Défis en géométrie
|
|
||
|
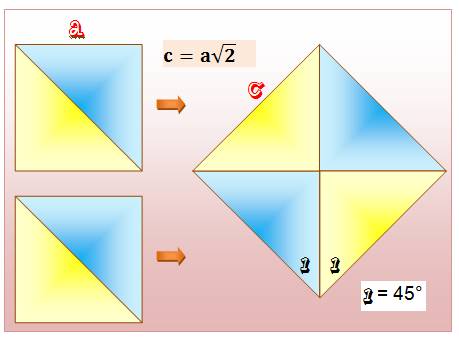
Deux carré en un Les
conditions d'assemblage en un grand carré sont évidentes. Aire du
grand carré: c² = (a Confirme
l'utilisation des deux petits carrés. |
|
|
|
Cinq carré en un Les
paramètres indiqués sur la figure permettent de confirmer les conditions
d'assemblage en un grand carré. Aire du
grand carré: c² = (a Confirme l'utilisation
des cinq petits carrés. |
|
|
|
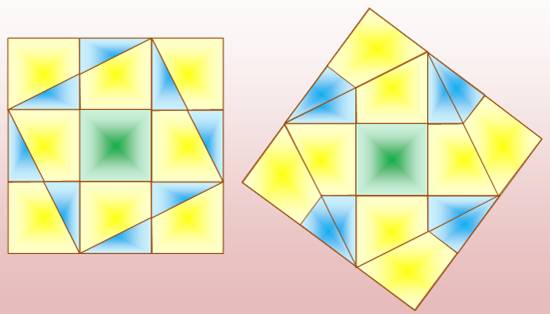
Neuf carrés en un Les
paramètres d'assemblage sont les mêmes que ci-dessus. Aire du
grand carré: c² = (3a)² = 9a² Confirme l'utilisation
des neuf petits carrés |
|
|
|
|
|
|
Il s'agit
de construire un grand carré à partir de trois carrés égaux ou,
réciproquement de découper un carré pour former trois carrés égaux en
assemblant les moreaux découpés. Ce
problème a été résolu par le mathématicien arabe médiéval Abu'l-Wafa' ( Sa
solution comporte 9 pièces. Au cours des siècles d'autres solutions avec 8, 7
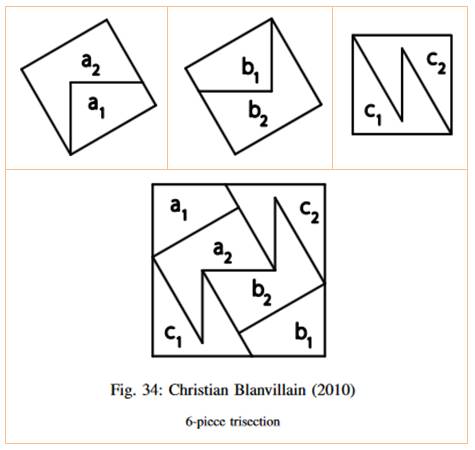
et même 6 pièces (Henri Perigal en 1891) ont été trouvées. Une nouvelle solution
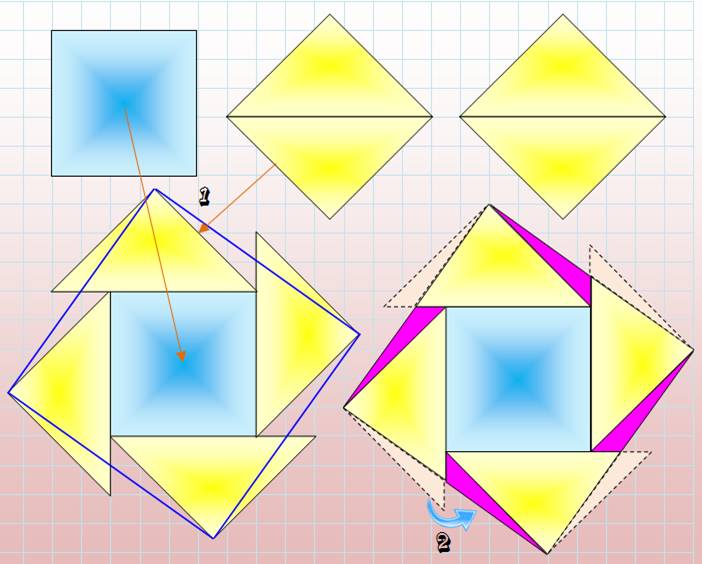
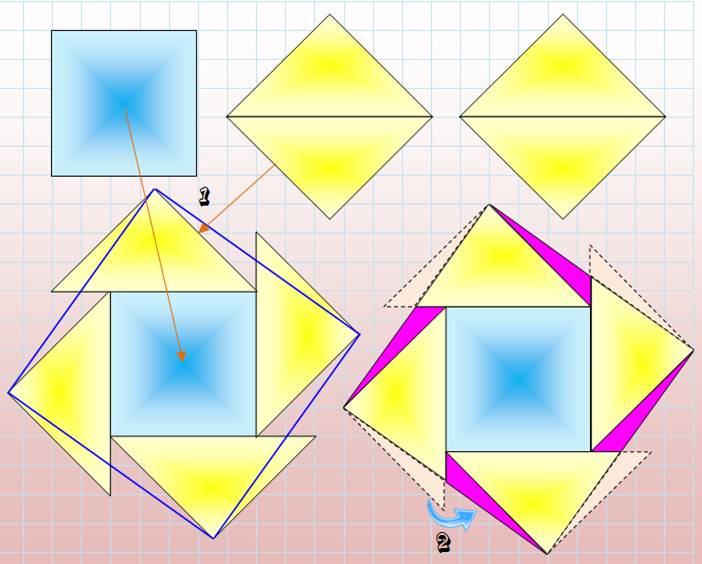
à 6 pièces avec grande symétrie a été trouvée par Christian Blainvillain en 2010. Trisection 1. Trois carrés égaux: un bleu et deux jaunes, ces deniers sont partagés
par une des diagonales et forment quatre triangles isocèles rectangles. 2. Les quatre triangles sont positionnés à la périphérie du carré bleu
comme indiqué sur la figure (1). 3. Les sommets sont réunis pour former le carré à bordure bleue. 4. Les petits triangles extérieurs (pointillés) sont rabattus (2) à
l'intérieur (mauves). 5. Le carré à bordure bleue est bien rempli par les trois carrés
initiaux. Figure
|
|
|
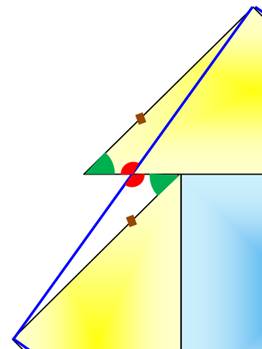
Assemblage correct (voir le détail
de la figure =>) Les
petits triangles sont bien
égaux et peuvent les uns combler les vides produits par les autres. En
effet:
Étant
démontré le bien fondé de l'assemblage, l'aire du grand carré est: c² = 3a² et la
longueur de son côté:
|
|
|
|
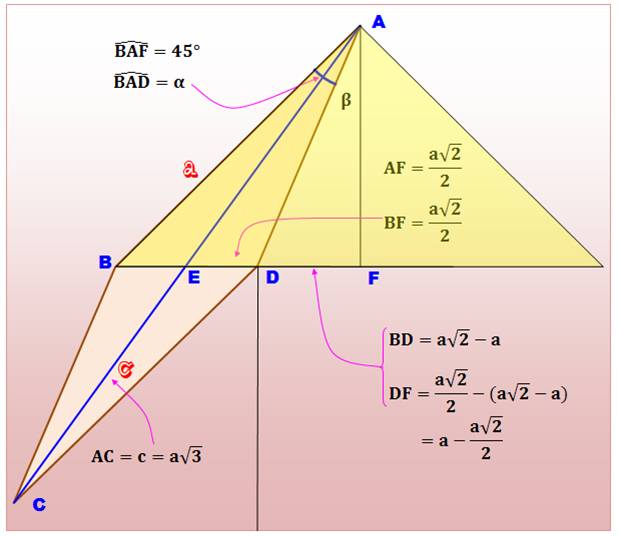
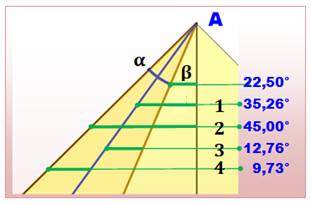
Angles dans les petits triangles Les
principales grandeurs ont été calculées et indiquées sur la figure. AB = a
est le côté du petit carré, et AC = c est le côté du grand carré. Notez que BD est la partie de la diagonale (a
BD et DF ne sont pas égaux. Par contre, ABCD est bien un losange.
..
|
||
|
Calcul des angles internes à alpha
Notez bien que les angles 3 et 4 ne sont pas égaux. |
|
|
Voir Angles
La
solution de Christian Blainvillain (2010)
|
|
Voir Référence,
notamment pour sa construction
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()