|
||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Étoile à cinq branches et nombre d'or
|
|
|
||
|
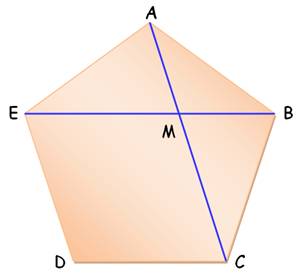
Pentagone
|
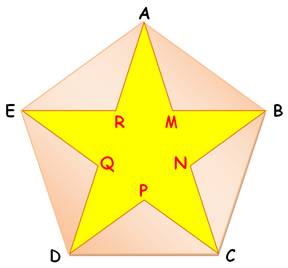
Étoile
|
|
|
|
||
Voir
Étoile à 5 branches / Fleurs à 5 pétales
|
|
|
|
|
|
Voir Angles du pentagone / Autres mesures du pentagone / Phi et médiatrice du pentagone / Décagone
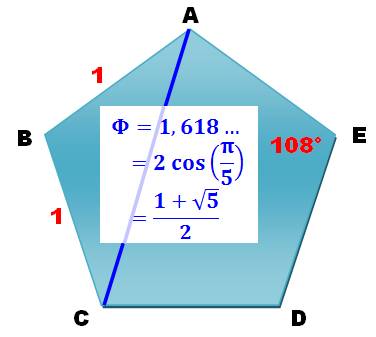
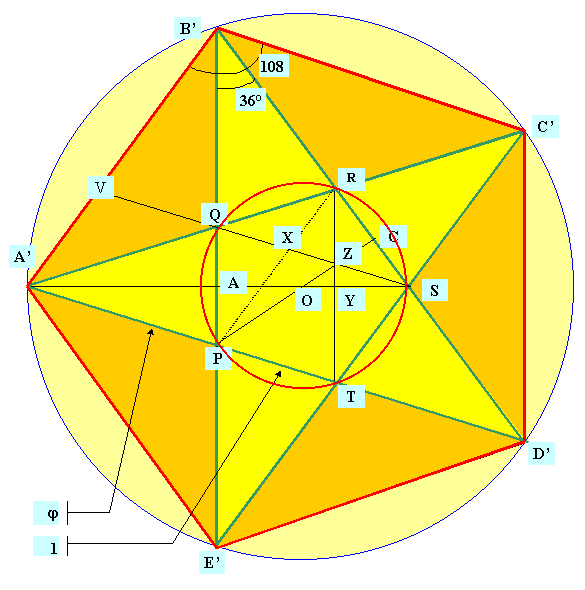
Nombre d'or dans le pentagone de côté unité
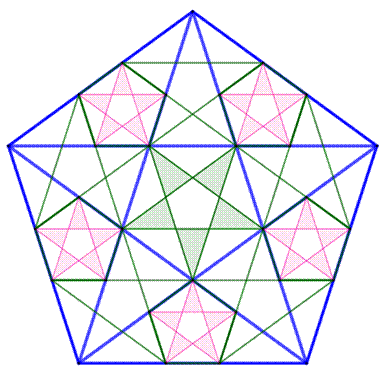
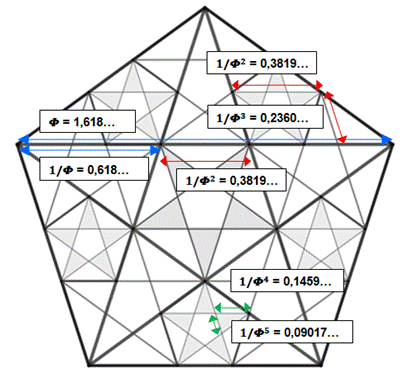
Voir Nombre d'or
et ses puissances / Série
et nombre d'or
|
|
||||||||||||||||||||||||||||||||||||||||
|
Angle au sommet: 108° = 2 cos(108°) = 1 –
On
prend PT = 1, alors A'P = F r = rayon du cercle qui inscrit le petit
pentagone P Q R S T R = rayon du cercle qui inscrit le grand
pentagone A'B'C'D'E' |
||||||||||||||||||||||||||||||||||||||||
|
Valeurs
Section
|
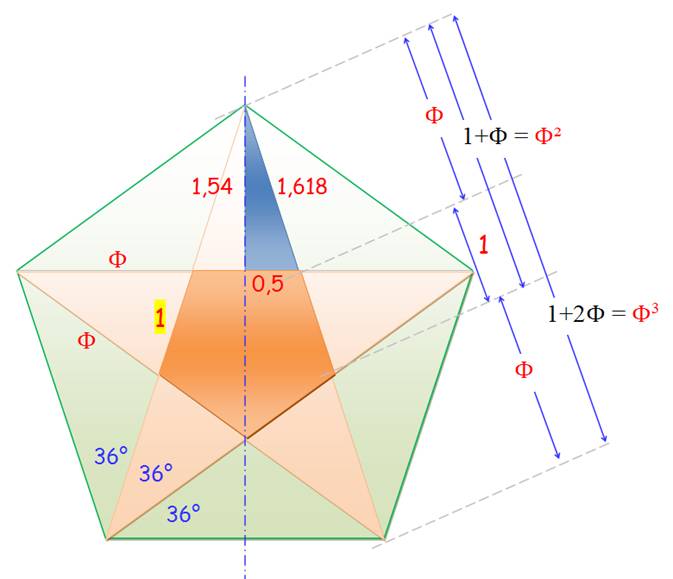
Rapports
Pyramide à base pentagonale Relevons tous les
sommets A', B', C', D' et E' en sommet H d'une pyramide
|
|||||||||||||||||||||||||||||||||||||||
|
Angle d'une branche d'étoile: 36 degrés = pi / 5 Cet angle trisecte
l'angle du pentagone: 3 x 36° = 108°. Les côtés des triangles isocèles
formant l'étoile sont en sections dorées avec la base. Chaque pointe est un triangle d'or. |
||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Retour |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrEtoi.htm |
![]()