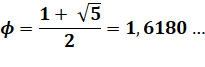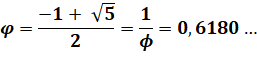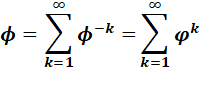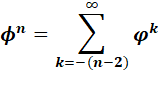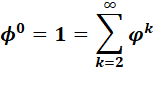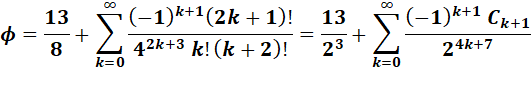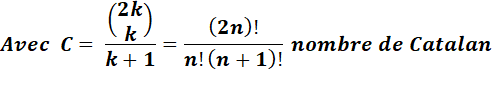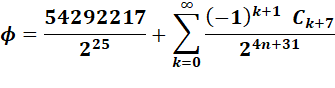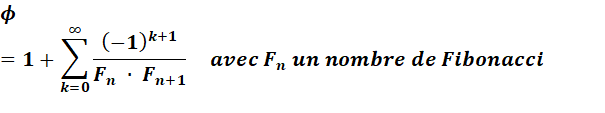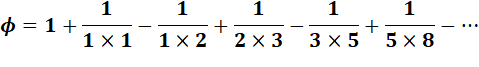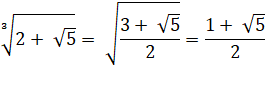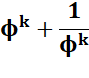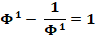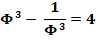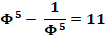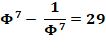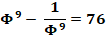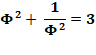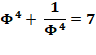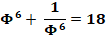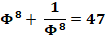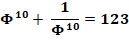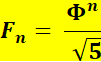NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 21/09/2022

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

        

Nombres

 

Débutants

Géométrie

NOMBRE D'OR

 

Glossaire

NOMBRE

D'OR

Tour d'horizon

Valeurs

Phi et Fibonacci

Proportion

Introduction

Formules

Puissances

Construction

Historique

Fraction continue

Trigonométrie

Géométrie

 

 

 

 

Sommaire de cette page

>>> PHI et ses puissances

>>> 1/ PHI et ses puissances

>>> Séries avec les inverses du nombre d'or

>>> Expressions avec radicaux

>>> Mêmes décimales

>>> PHI et 1/PHI et puissances

>>> Phi puissance n est un quasi-entier

>>> Calcul de Fn

>>> Calcul avec la valeur approchée

 

 

 

 

NOMBRE d'OR en PUISSANCE

 

La magie du nombre Phi = 1,618…

Magie que l'on retrouve dans l'étoile à cinq branches

 

 

PHI et ses puissances

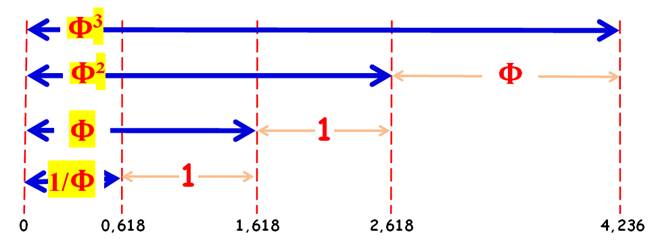
Φ

= 1 + 1 / Φ  = (1 + Φ )

= 1, 618 ...

Φ 2

= Φ  + 1

= 2, 618 ...     Voir Méthode

Φ 3

= Φ 2 + Φ  = 2 Φ  + 1

= ( Φ  + 1) / ( Φ  - 1)

= 4, 236 ...

= nombre de cuivre

Φ 4

= 3 Φ  + 2

= 6, 854 ...

Φ 5

= 5 Φ  + 3

= 11, 090 ...

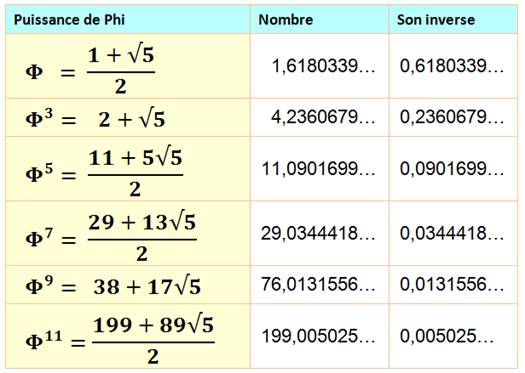
Φ n

= Φ n-1 + Φ n-2

Somme des deux précédents

Φ n

= Fn Φ  + Fn-1

Fn = nombre de la suite deFibonacci

Voir Pentagones gigognes

 

Puissances du nombre d'or, Fibonacci et Lucas

  

Voir Brève 792 / Fibonacci et Lucas

 

 

 

Inverse de PHI et ses puissances

-1 /   Φ

= 1 - Φ

= - 0, 618 ...

(-1/ Φ )2

= 1 - 1 / Φ

= 0, 3819 ...

1 /   Φ

= Φ  - 1

= 0, 618 ...

1 / Φ 2

= 1 - 1 / Φ  = 2 - Φ

= 0, 3819 ...

1 / Φ 3

= 2 / Φ  - 1 = 2 Φ  - 3

= 0, 236 ...

1 / Φ 4

= 2 - 3 / Φ  = 5 -3 Φ

= 0, 145...

1 / Φ n

=    Fn+1  – Fn Φ  

= – Fn+1  + Fn Φ

pour n pair

pour n impair

Voir Séries avec les inverses du nombre d'or

 

 

 Quelques relations et séries avec le nombre d'or

 

 

 

 

 

 

Trois formules plus étranges ! (déduites de séries de Taylor)


Cette formule produit dix chiffres significatifs pour k = 10.

 

 

 

 

 

 

Voir Nombre d'or et séries / Nombres de Catalan / Nombres de Fibonacci

 

PHI et ses puissances avec radicaux

 

*    Il n'est pas étrange de voir toutes les puissances de PHI et 1/PHI exprimées avec la racine de 5.

*    Notez qu'il est moins évident de reconnaître:

*    Pour la racine carrée, cette relation repose sur l'identité remarquable:

 

 

Table des puissances de 1 à 10 de PHI et 1/Phi

 

*    Notez que les coefficients sont les nombres de la suite de Fibonacci.

*    Notez également que les deux termes ajoutés sont chacun voisins de la moitié de la somme. >>>

 

Voir Calculs avec radicaux – Exemples du nombre d'or

Merci à Lucas M.

 

 

Mêmes décimales

pour Phin et son inverse

 

*    Phi et son inverse ont les mêmes décimales

*    C'est le cas également pout toutes les puissances impaires de Phi. 

 

Voir Mêmes décimales

 

 

PHI et 1/PHI et puissances

Φ n + 1/ Φ n

n pair

= Fn Φ  + Fn-1 + Fn+1  – Fn Φ

= Fn-1 + Fn+1 

Somme de deux entiers = entier

Φ n  + 1/ Φ n

n impair

= Fn-1 + Fn Φ  – Fn Φ + Fn+1 

= Fn-1 + Fn+1 

Somme de deux entiers = entier

Φ n

Car 1/ Φ n tend vers 0 dans les deux formules ci-dessus.

 

 

 

 

prend des valeurs entières pour k pair.

 

 

 

La différence pour une puissance k impair ou la somme pour k pair est un nombre entier.

 

Par exemple jusqu'à 10:

 

 

Notez que, comme pour la suite de Fibonacci, chaque nombre est la somme des deux précédents.

 

 

Valeurs de Fn : presque entier

 

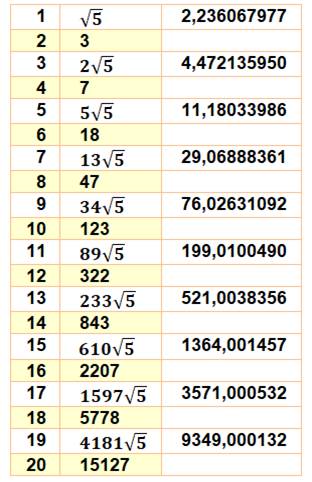
                       n         Φ n                                 Écart avec l'entier proche

                             1            1,  618033988                 –     0, 3819

                             2            2,  618033988                 –     0, 3819

                             3            4,  236067977                        0, 2360

                             4            6,  854101966                 –     0, 1458

                             5            11,  09016994                        0, 0901

                             6            17,  94427190                 –     0, 0557

                             7            29,  03444185                        0, 0344

                             8            46,  97871376                 –     0, 0212

                             9            76,  01315561                        0, 0131

                           10            122,  9918693                 –     0, 0081

                           11            199,  0050249                        0, 0050

                           12            321,  9968943                 –     0, 0031

                           13            521,  0019193                        0, 001919

                           14            842,  9988137                 –     0, 001186

                           15            1364,  000733                        0, 000733

                           16            2206,  999546                 –     0, 000453

                           17            3571,  000280                        0, 000280

                           18            5777,  999826                 –     0, 000173

                           19            9349,  000106                        0, 000106

                           20            15126,  99993                 –     0, 000066

 

Plus la puissance est élevée plus la valeur se rapproche d'un entier.

 

 

Pour information:

n = 100  on a vingt fois le 9.

Phi100 = 792070839848372253126,999999999999999999998737488…

Écart = -0,126… 10-20

n = 1000, on a 207 fois le 9

Phi1000 = 97194177735908175207 981982 079326473 737797879 155345685 082728081 084772518 8184448152 6908061914 9045968297 679578305 403209347 4011630369 0766057397 1740862463 7518016412 0149028409 7309096322 6815316757 0766669532 3797578126,

           99999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999 9999999999    897113

Écart =  -0,103… 10-208

 

Racine de 2

Le même phénomène de presque entier se retrouve avec (1 + ) n.

Pour la puissance 20, on trouve: 45 239 073,999999977895.

 

Voir Nombres presque entiers

 

 

 

Calcul de Fn – Nième terme de la suite de Fibonacci

Φ n – 1/ Φ n

n pair

= Fn Φ  + Fn-1 – Fn+1  + Fn Φ

= 2Fn Φ + Fn-1 – Fn+1 

Φ n  – 1/ Φ n

n impair

= Fn-1 + Fn Φ  + Fn Φ – Fn+1 

= 2Fn Φ + Fn-1 – Fn+1 

Φ n  – 1/ Φ n

n

= 2Fn Φ + Fn-1 – Fn+1 

= 2Fn Φ + Fn-1 – (Fn +  Fn-1)

= 2Fn Φ + Fn-1 – Fn  –  Fn-1)

= Fn (2Φ – 1)

= 5 Fn

Valeur exacte

Φ n  – 1/ Φ n = 5 Fn

Valeur approchée

Φ n  = 5 Fn

 

 

Calcul avec la valeur approchée

 

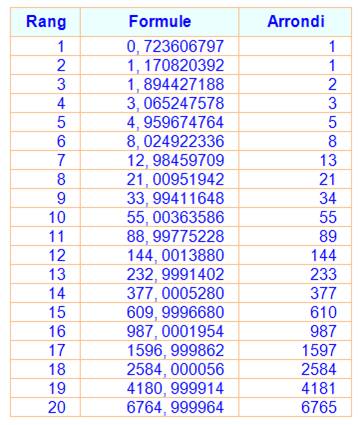
Calcul d'un nombre de Fibonacci de rang n

 

C'est la valeur arrondie des puissances de Phi, calculée ci-dessus, divisées par racine de 5.

Exemples:

 

 

 

 

 

Suite

*    Formules

*    Construction

*    Divine proportion

*    Nombre d'or dans le pentagone

*    Autres valeurs dans le pentagone

Aussi

*    Cercle

*    Constante Pi

*    Constantes Mathématiques

*    Série du type Fibonacci et cousins

DicoNombre

*    Nombre 1,618…

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrPuis.htm