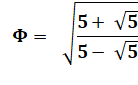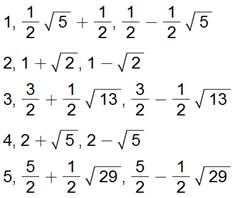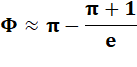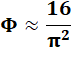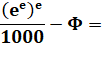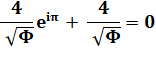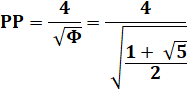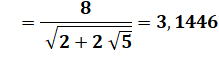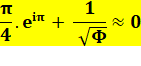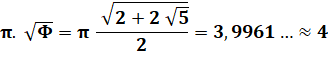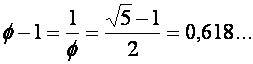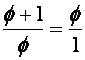|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRE
d'OR – Valeurs
= 1,118… + 0,5 La somme
de ses 146 premières décimales de Phi est égale à 666, ce qui en fait un nombre
du diable. Depuis
septembre 2018, cette constante est connue avec 2 600 milliards de décimales (Tizian Haaselmann). |
Valeurs de Phi et
commentaires
|
Φ = ( 1/ Φ = ( |
|
|
Φ + 1/ Φ
= 2 Φ – 1
= =
2, 236 067 977 … |
|
|
Φ = 5.5 x .5 + .5 Φ = 5 ^ .5 * .5 + .5 Φ = 2, 236 067
977 … x 0,5 + 0,5 =
1, 118 033 988… + 0,5 =
1, 618 033 988… |
Voir Jeux
|
|
|
|
|
|
|
|
1,618 033 98 … avec 8 décimales |
Voir Mnémotechnique |
|
1,6180339887
49894848 … |
|
|
Nombre d'or avec 1 024
décimales |
|
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
1076738937 6455606060
5921... Notez que 1/Phi vaut la même chose en remplaçant le 1 initial par 0. |
|
|
|
||
|
Ce qui veut dire, par exemple, que diviser
un nombre par Phi est équivalent à le multiplier par 0,618…, ce qui est plus
facile à exécuter.
x² - nx – 1 = 0
|
|
|
Voir Suite binaire dorée
|
|
||
|
|
=
1,617985… (0,00005) Approximation avec |
|
|
|
=
1,6211 (0,0031) |
|
|
|
=
1,666 … (0,05) |
|
|
|
=
1,600 … (0,02) |
|
|
|
=
1,618 055 … (0,000 02) |
|
|
|
=
1,618 025 751 … (0,000 008) |
|
|
|
=
0,625 |
|
|
|
=
0,00014400… |
|
|
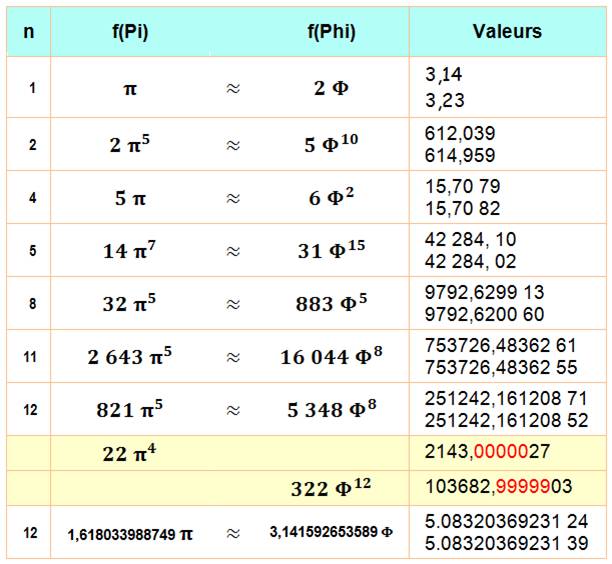
Le
fait que Pi soit proche de 2 Phi incite à chercher une relation plus
approchée de ces valeurs.
Prenons
le logarithme en supposant l'égalité:
Formule
pour le calcul de b qui donne l'égalité
Voici
quelques résultats de calcul avec n décimales exigées:
Les
deux lignes en jaune donnent des valeurs presque entières avec Pi et avec
Phi. La
dernière ligne montre les limites d'un tel exercice. Une égalité à n
décimales est obtenue en multipliant chacun par le nombre formé des n
chiffres de l'autre. |
|
|
||
|
Une approximation originale qui allie ces cinq nombres. |
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 0,785398… + 0,786151… = 0,00075… |
|
|
|
|
|
Merci à Ûllah G.
|
|
|
|
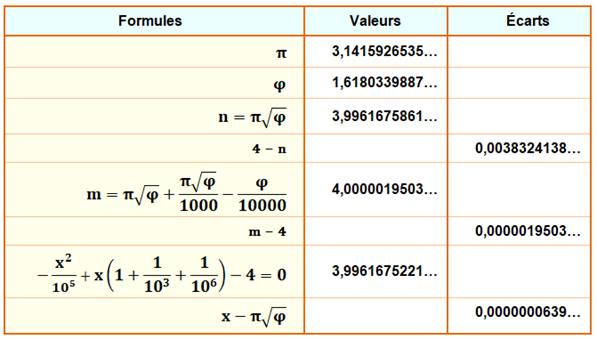
Le produit 𝛑√φ est voisin
de 4 à 0,1%. Il est possible d'approcher la valeur 4 avec la formule notée m. L'équation en x, trouvée par José Luis Cruz, produit une excellente
approximation de 𝛑√φ.
|
|
Merci à José Luis Cruz.
|
Valeurs des racines des
équations: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(en gras, les racines)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
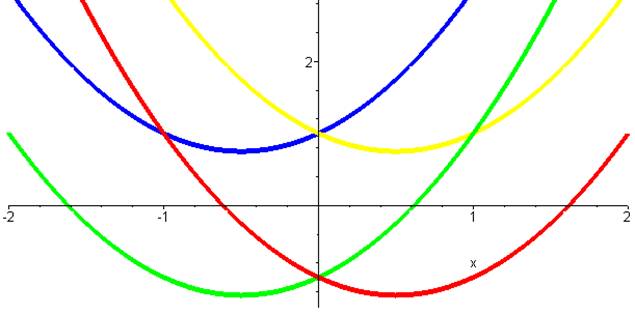
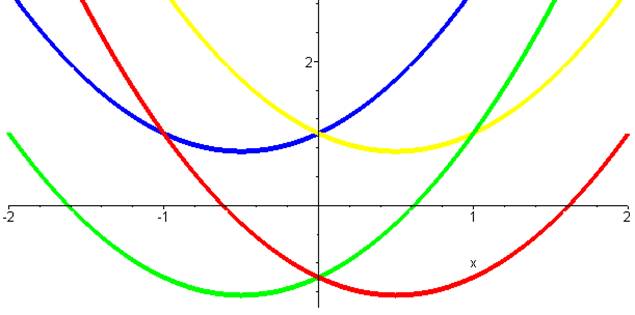
Pour l'amusement, observons
les quatre fonctions possibles
- 1,618 -
0,618 0,618 1, 618
|
|
|
Le nombre d'OR est
irrationnel –
Démonstration |
|
||
|
Supposons que le
nombre d'or x soit rationnel, c'est-à-dire égal à une fraction p/q. On suppose que les
nombres entiers p et q sont choisis de manière que la fraction soit la
plus simplifiée possible. Autrement dit, p
et q n'ont pas de facteur commun. Ou encore: p
de divise par q, pas plus que q ne divise p. (Pour les matheux:
leur plus grand commun diviseur est égal à 1). |
x PGCD (p,q) |
= p/q = 1 |
|
|
Le nombre d'or est
défini par l'équation. |
x² – x – 1 |
= 0 |
|
|
En y introduisant
la valeur rationnelle de x. |
(p/q)² – (p/q) – 1 |
= 0 |
|
|
En multipliant par q². |
p² – pq – q² p( p – q) |
= 0 = q² |
|
|
En divisant par p. |
p – q |
= q² / p |
|
|
Le membre de gauche
est un entier En conséquence
celui de droite doit l'être aussi. Mais est-ce bien
vrai? |
p – q q² / p |
= entier = entier ? |
|
|
Eh bien non! p
ne peut pas diviser q. Ce serait contraire
à notre hypothèse de départ. |
p et q |
Aucun facteur commun |
|
|
Cette contradiction
montre qu'il n'est pas possible d'écrire le nombre d'or sous forme de
fraction. |
Le nombre d'or |
est irrationnel |
|
|
|
||
|
1
618 033 est premier
avec sept chiffres. 1618
… avec 13, 255, 280 … chiffres sont aussi des
nombres premiers |
61 est premier avec deux chiffres 618 … avec 14, 887 … chiffres sont aussi des nombres premiers |
|
![]()
|
Suite |
|
|
Aussi |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()
Renvois de
liens