NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/09/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Carrés magiques
Débutants Carrés magiques	Carré magique 4 x 4			Glossaire Carrés magiques
INDEX Carrés magiques	Carré 4 x 4	Décompte	Formules
	Premiers	Cousinage	Relations	Pandiagonaux
		Sommaire de cette page >>> Carré de Dürer >>> Principe de codage >>> Dénombrement >>> Toutes les configurations magiques >>> Carré de Dürer en binaire

QUANTITÉ de SOMMES MAGIQUES

dans un carré magique

Exemple sur le carré magique diabolique

d'ordre 4 de Dürer.

Propriétés diverses et dénombrement des somme magiques.

Carré MAGIQUE & DIABOLIQUE de Dürer

· Ce carré figure sur le tableau "Mélancolie" peint par Albrecht Dürer en 1514.

· Outre les sommes constantes sur les lignes, colonnes et diagonales, ce carré présentent de nombreuses configurations de 4 carrés donnent aussi la constante magique 34:

Les quatre coins donnent 34.

Les quatre au centre aussi.

Chaque carré 2x2 en coin donne aussi, comme 16 + 3 + 5 + 10 = 34.

De même pour 2, 3, 15, 14.

Etc.

· Par contre, il n'est pas pandiagonal, même si une pandiagonale sur deux donne la somme 34.

· En revanche, il est associatif: la somme des extrémités diamétralement opposées vaut la demi-constante magique:17.

Cliquez pour image complète

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

Voir Carré de la Sainte Famille / Carré doublonné

Notez l'arrangement hexagonal des nombres pairs et impairs

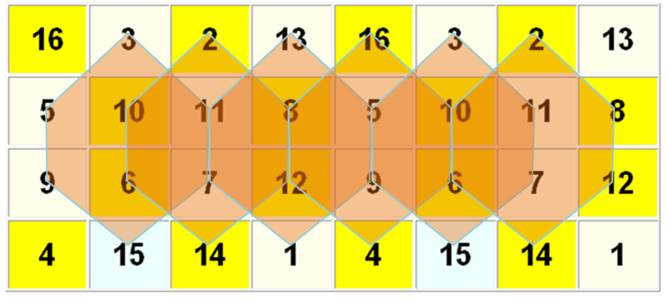
Voir Hexagone / Hexagones magiques / Pair-Impair

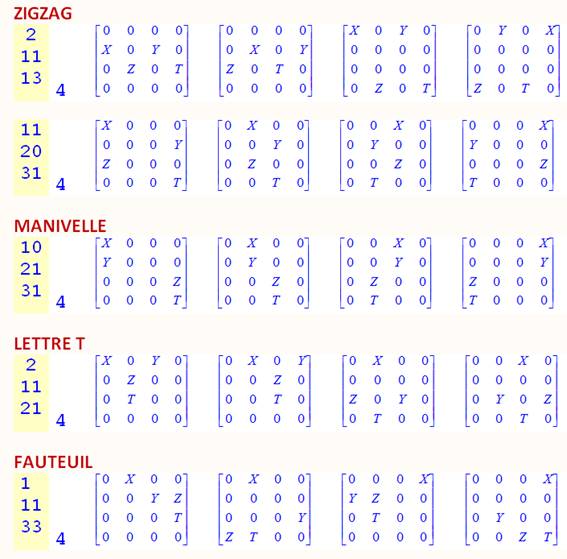
Dénombrement des cas de constantes magiques

· On montre le premier cas et, on indique la quantité de combinaisons du même type, obtenues par translations ou symétries:

X	X
X	X

1

X	X
X	X

1

X	X
X	X

4

X	X
X	X

4

X	X
X	X

2

	X
X
			X
		X

2

X	X
		X	X

4

X	X
X	X

4

Total sur ce tableau

Sommes classiques: 10

Sommes particulières: 22

· On va voir qu'il y en a beaucoup plus, mais pour les identifier et les dénombrer, il faut une méthode.

Symétrie des sommes deux à deux
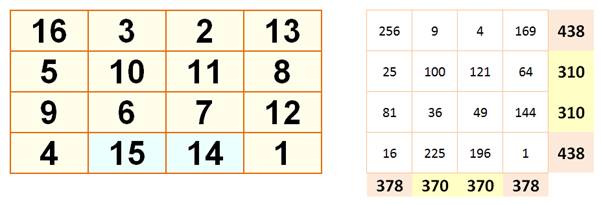
Somme des carrés
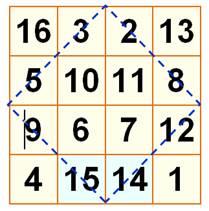
Losange Somme magique sur le carré incliné (pointillés bleus) 5 + 3 + 12 + 14 = 2 + 8 + 15 + 9 = 34 Les carrés 5^2 + 3^2 + 12^2 + 14^2 = 2^2 + 8^2 + 15^2 + 9^2 = 11 x 34 = 374 Les cubes 5^3 + 3^3 + 12^3 + 14^3 = 2^3 + 8^3 + 15^3 + 9^3 = 136 x 34 = 4 624

Voir Autres sommes multi-puissantes

Principe de codage

ou comment définir une configuration magique?

· L'idée consiste à partir de la case la plus en haut à gauche et de définir les trois autre à partir de celle-là. En relatif, donc.

· Pour chacune des trois on forme un nombre à deux chiffres dont celui des dizaines donne le mouvement en descente et celui des unités celui vers la droite.

X
		Y

Code: 12, car pour passer de X à Y,

il faut descendre de 1

et avancer de 2.

· Pour coder une configuration magique, il faut trois nombres.

· Dans le cas où on reste sur la même ligne, la dizaine qui vaut 0 est sous-entendue.

· Pour faciliter le repérage, un nom est donné à la forme. ici, ce serait l'équerre.

X	Y
		Z
		T

Code: 1, 12, 22

Figure: équerre

Dénombrement

· Ce premier tableau donne le nom de la configuration magique et leur quantité dans tout le carré magique.

LIGNES	4
COLONNES	4
DIAGONALES	4
CARRÉ 2 x 2	8
CARRÉ 3 X 3	4
RECTANGLE	8
LOSANGE	8
ESCALIER	4
ÉQUERRE	8
ZIGZAG	8
MANIVELLE	4
LETTRE T	4
FAUTEUIL	4
ESCALIER À PALIER	4
AUGE	4
CROIX	4
LETTRE GRAND V	2
Total	86

· Note: le total des configurations magiques ou non est égal à la quantité de tirages de 4 cases parmi 16, sans ordre, soit:

Toutes les configurations magiques
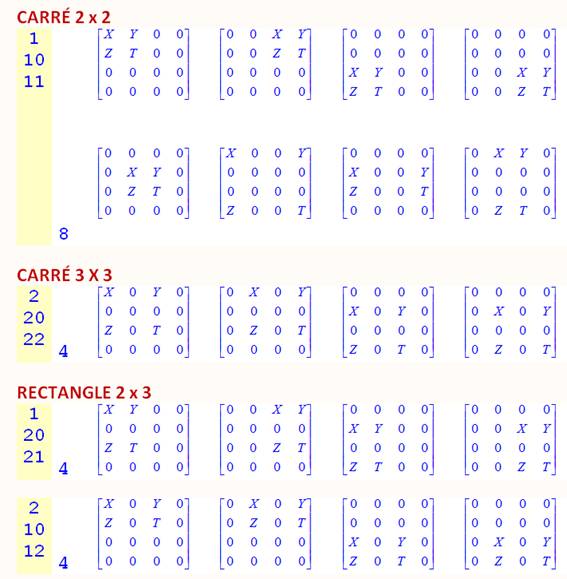
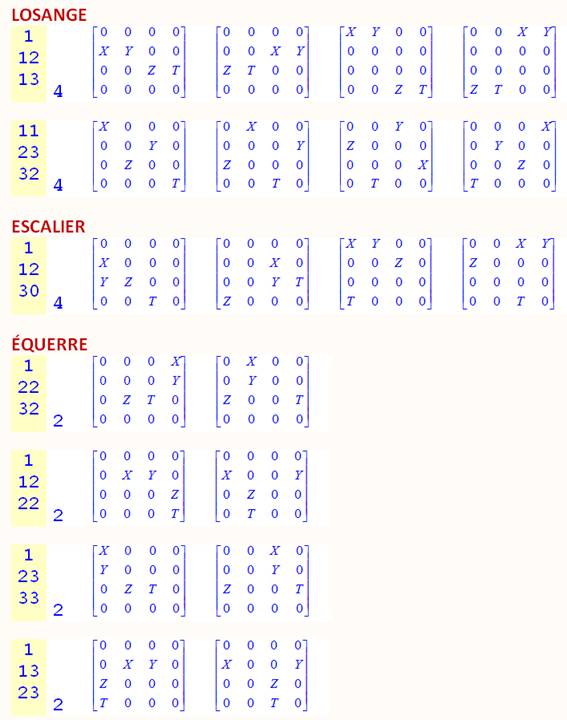
· Voici le détail des configurations avec leur code. Vous mesurerez l'intérêt du code en comparant les configurations ayant le même code. Pas évident de reconnaître la similitude du premier coup d'œil. · On donne le code (case jaune), la quantité de configurations les configurations.

Carré de Dürer en binaire

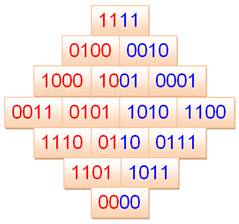
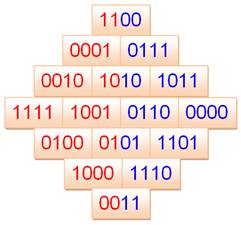
Transposition

Les seize nombres du carré de Dürer sont transposés en binaire.

Il nous faut les seize positions de 0000 à 1111 qui codent normalement des nombres décimaux de 0 à 15.

Pour passer des nombres de 1 à 16 du carré magiques nous ferons moins un sur chacun de ces nombres.

Propriétés

Les deux nombres aux extrémités des diagonales (longues ou courtes) sont l'image inverse l'un de l'autre: un 0 devient 1 et un 12 devient 0. Exemple avec 1111 qui devient 0000 ou 0010 qui devient 1101.

Il existe une symétrie lors des rotations de 45°.

Avec la rotation négative, la moitié du carré est comme l'image dans un miroir de l'autre moitié.

Avec la rotation positive, la moitié du carré est comme l'image inversée dans un miroir de l'autre moitié.

Carré transposé en binaire

16 1111	3 0010	2 0001	13 1100
5 0100	10 1001	11 1010	8 0111
9 1000	6 0101	7 0110	12 1011
4 0011	15 1110	14 1101	1 0000

Rotation -45°

Rotation 45°

Selon Mark Collins rapporté par Clifford Pickover

Suite	Carré 4 x 4 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dénombrement Dominos magiques Géométrie Humour Jeux Nombres magiques - Index Pannumérique Rubriques débutants Sudoku
Diconombre	Nombre 34
Sites	Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/Decompte.htm