NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Carré magique 8 x 8				Glossaire Carrés magiques
INDEX Carrés magiques Ordres Constructions Magie Jeux de grilles Jeux et énigmes	Carré 8 x 8		Bimagique	Construction diagonale
	Additif et multiplicatif		Gigogne	Carré de Benjamin Franklin
		Sommaire de cette page >>> CARRÉ MAGIQUE D'ORDRE 8 >>> Construction par les diagonales >>> Construction matricielle >>> Construction serpentin >>> Construction serpentin originale >>> Carrés magiques gigognes d'ordre 8 >>> Carré magique plus que parfait >>> Autres carrés 8 x 8

CARRÉS MAGIQUES

d'ordre 8

dont le fameux carré magique d'ordre 8 de Benjamin Franklin

CARRÉ MAGIQUE D'ORDRE 8

Somme magique

Nombres de 1 à 8² = 64

Somme de tous les nombres de 1 à 64 = ½ (64 x 65) = 2 080

Somme magique: 2 080 / 8 = 260

Exemple: carré de Yukio Yamamoto (1972)

1	32	35	62	49	48	19	14
56	41	22	11	8	25	38	59
10	23	44	53	58	39	28	5
63	34	29	4	15	18	45	52
13	20	47	50	61	36	31	2
60	37	26	7	12	21	42	55
6	27	40	57	54	43	24	9
51	46	17	16	3	30	33	64

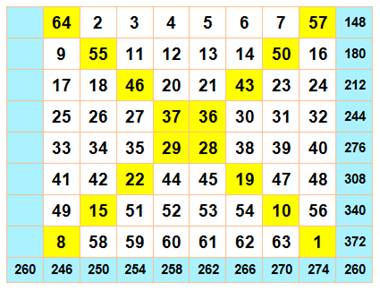
Carré magique diabolique

En jaune les nombres de 1 à 34

Carré 8 x 8

Ce carré est associatif complet: les extrémités des diamètres sur chaque couronne donnent une somme de 65.

Il est pandiagonal

Carrés 6 x 6

La somme des quatre coins des 9 carrés de 6 x 6 donnent la somme 130

Carrés 4 x 4

Les 4 carrés 4 x 4 sont semi-magiques: toutes les demi-lignes et demi-colonnes donnent la somme 160.

La somme des quatre coins des 16 carrés de 4 x 4 donnent la somme 130.

Carrés 2 x 2

Les 7 x 7 = 49 petits carrés de 2 x 2 somment à 130.

Les quatre coins donnent aussi 130.

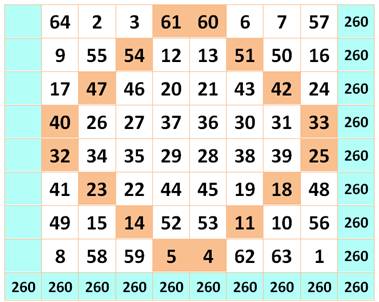
Un autre exemple avec structure interne particulière

18	19	38	39	10	11	62	63
17	20	37	40	9	12	61	64
14	15	58	59	22	23	34	35
13	16	57	60	21	24	33	36
55	54	3	2	47	46	27	26
56	53	4	1	48	45	28	25
43	42	31	30	51	50	7	6
44	41	32	29	52	49	8	5

Carré magique panmagique

Construction d'un CM d'ordre 8 Méthode des diagonales
Trois étapes simples: lister les nombres de 1 à 64 dans les cellules du carré; inverser chacune des grandes diagonales (jaune); et inverser les semi-diagonales indiquées (marron)

Voir Construction d'un CM d'ordre 4 / Brève 53-1056

Construction matricielle
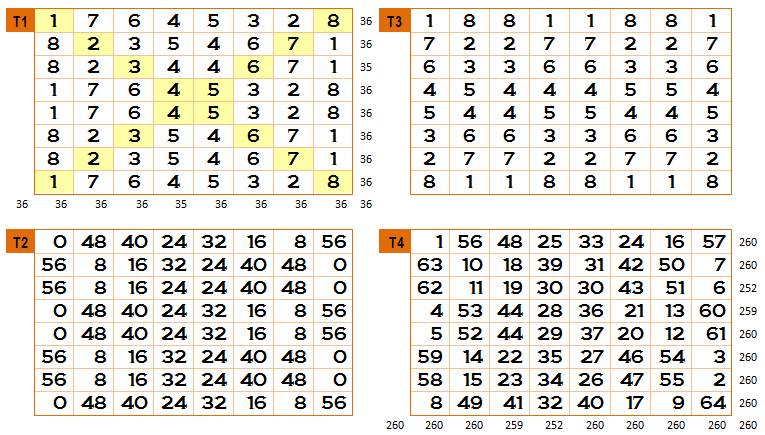
Tableau 1	Un carré latin: nombre de 1 à 8; sommes 36 sur lignes, colonnes et diagonales
Tableau 2	Tableau 1 dont chaque case est multipliée par 8 et on y retranche 8.
Tableau 3	Tableau 1 transposé: lignes deviennent colonnes. Autrement-dit, le tableau a pivoté de 90°. Résultat: les couples de nombres de cases correspondantes sont tous présents et jamais dupliqués. Carrés latins orthogonaux ou gréco-latins.
Tableau 4	Chaque case du carré magique est la somme des cases correspondantes des tableaux 2 et 3.

Voir Méthode générale / Construction du carré 6x6

Construction serpentin
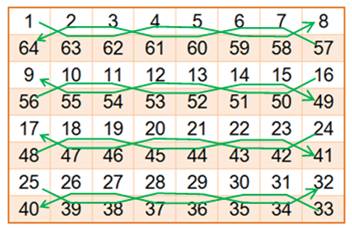
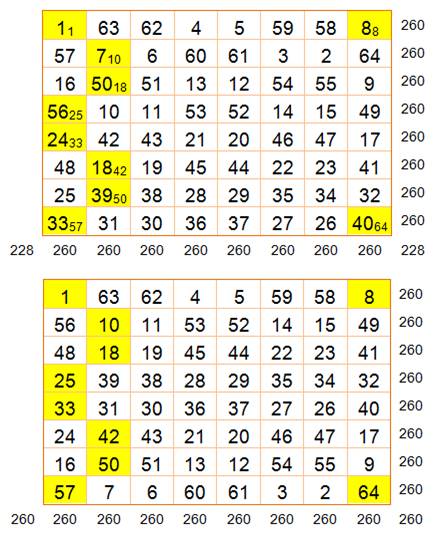
Les nombres de 1 à 64 sont placés dans la grille selon le serpentin indiqué: saut de ligne sur deux; progression de gauche à droite puis de droite à gauche. Marquage des chemins en vert. La somme sur un chemin est la constante magique (260). Le sens est indiqué. Il pourra être déduit de la suite s'il y a erreur. Les nombres sont replacés dans la grille en dépliant la ligne verte de sorte que chaque ligne droite donne la constante magique. Les case marquées en jaune sont des invariants. Le nombre qui doit y être placé est celui qui viendrait normalement en remplissant la grille avec les nombres successifs (nombres placés en indice). Les lignes sont déplacées pour respecter les nombres imposés par les invariants. Finalement, le carré est magique, y compris ses diagonales. Il est même associatif: la somme de deux nombres symétriques par rapport au centre est constante. C'est le même que celui construit avec la méthode diagonale. Voir Principe de la méthode
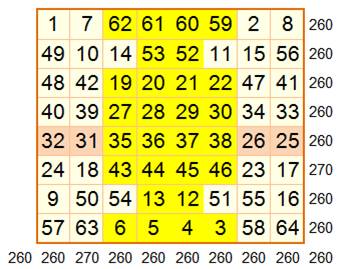
De nombreux carrés magiques 8x8 sont possibles en pratiquant d'autres choix pour les lignes vertes. Certains passionnés ont établi les tableaux des trajets qui marchent. Celui-ci est un exemple. Remarquez la régularité des nombres qui se suivent (couleurs).

Construction serpentin originale – 402 fois magique!
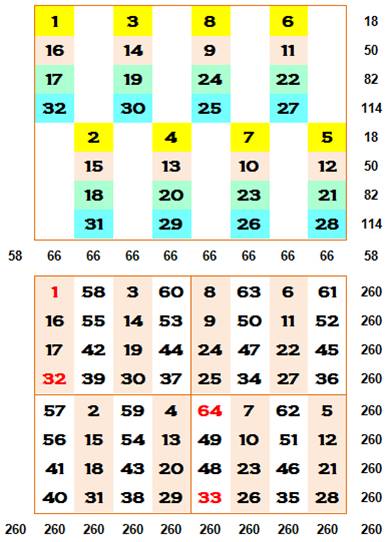
Le carré est rempli initialement avec les nombres de 1 à 32 en suivant le schéma indiqué. Arrangement sympathique, mais il fallu le trouver! La suite est très simple: chaque nombre de ce premier carré est translaté dans le carré final: translation de quatre pas en diagonale vers la droite et vers le bas. le nombre à placer est celui du départ complément à 65. Comme d'habitude, on imagine le carré enroulé sur lui-même pour placer les nombres qui débordent. Exemple (en rouge): Le nombre 1 devient 64, car 1 + 64 = 65. Le nombre 32 devient 33, car 32 + 33 = 65.
Ce carré magique est assez spectaculaire. Il a bien entendu sa propriété de construction. Il est panmagique: toutes les diagonales, classiques ou restituées par enroulement, donnent la somme magique. Il est également magique sur les "diagonales penchées", celles engendrées par le mouvement du cavalier	Magique; Somme 65 sur les diagoanles de longueur 4 (par construction); Panmagique: un fou qui avance huit fois sur cette grille parcourt 260 points; et Extra-panmagique: un cavalier qui avance huit fois selon le même mouvement parcourt 260 points. On retrouve ainsi: 2 x 8 + 2 (magique) + 2 x 8 x 8 (panmagique) + 16 x 16 (cavalier) = 402 sommes magiques.

Carré magique 8x8 plus que parfait (ou enchanté)
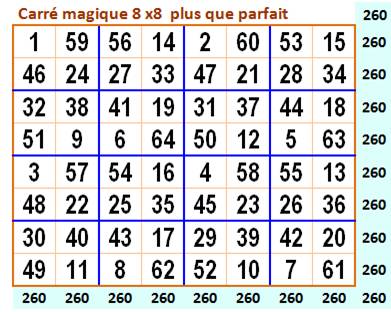
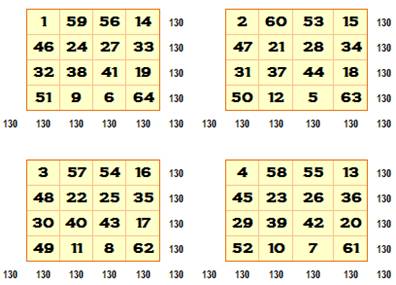
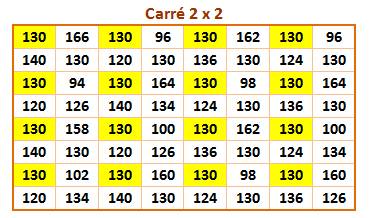
Un carré magique plus que parfait est tel que les seize carrés 2x2 présentent la même somme, en fait, la demi-constante magique: 130. Ce carré magique n'est ni panmagique (non-magique sur les diagonales secondaires), ni associatif (somme des sommets des diamètres). Mais il a de sérieux atouts (ou atours). Les quatre quarts de ce carré sont des carrés 4x4 magiques et associatifs. Le tableau "carré 2x2" montre les sommes sur tous les carrés 2x2 du carré magique, y compris ceux obtenus par enroulement du carré. En jaune les carrés jointifs. Exemples: 130 = 1 + 59 + 46 + 24 Le suivant: 166 = 59 + 56 + 24 + 27. Une grande majorité des sommets des carrés 3x3 somment en 130. Exemples: 1 + 56 + 32 + 41 = 130 Le suivant: 59 + 14 + 38 + 19 = 130. Une autre propriété inattendue avec les sommets des carrés 5x5 qui sont quatre nombres successifs. Exemples: 1, 2, 3, 4 Le suivant: 59, 60, 57, 58	Carrés 4x4

Voir Carré plus que parfait d'ordre 4

Carrés magiques gigognes d'ordre 8

19	25	26	41	42	43	44	20
27	9	54	53	52	17	10	38
30	14	1	63	62	4	51	35
32	18	60	6	7	57	47	33
34	49	8	58	59	5	16	31
36	50	61	3	2	64	15	29
37	55	11	12	13	48	56	28
45	40	39	24	23	22	21	46

Les carrés centraux d'ordre 4 et 6 sont aussi magiques de somme 130 et 195.

Autres carrés magique d'ordre 8

1	48	31	50	33	16	63	18
30	51	46	3	62	19	14	35
47	2	49	32	15	34	17	64
52	29	4	45	20	61	36	13
5	44	25	56	9	40	21	60
28	53	8	41	24	57	12	37
43	6	55	26	39	10	59	22
54	27	42	7	58	23	38	11

La somme de chaque demi-ligne est 130 et en traçant le suivi des chiffres croissants, on obtient une figure géométrique régulière:

Voir carrés magiques et semi-magiques avec l'échiquier

Autres exemples

1	58	3	60	61	6	63	8
16	55	14	53	52	11	50	9
17	42	19	44	45	22	47	24
32	39	30	37	36	27	34	25
40	31	38	29	28	35	26	33
41	18	43	20	21	46	23	48
56	15	54	13	12	51	10	49
57	2	59	4	5	62	7	64

64	9	17	40	32	41	49	8
2	55	47	26	34	23	15	58
3	54	46	27	35	22	14	59
61	12	20	37	29	44	52	5
60	13	21	36	28	45	53	4
6	51	43	30	38	19	11	62
7	50	42	31	39	18	10	63
57	16	24	33	25	48	56	1

Bonus

Suite	Carré magique de Benjamin Franklin Biographie de Benjamin Franklin Carré magique premier d'ordre 8 Carré bimagique Carré d'ordre 9 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Énigmes Jeux Nombres en chiffres Nombres magiques - Index Rubriques débutants Sudoku
Diconombre	Nombre 8 Nombre 64 Nombre 260
Sites	Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordre8.htm