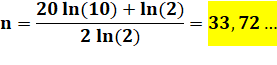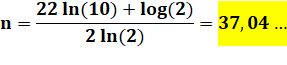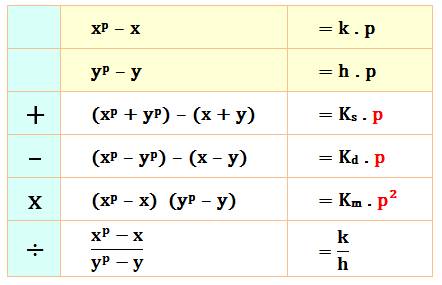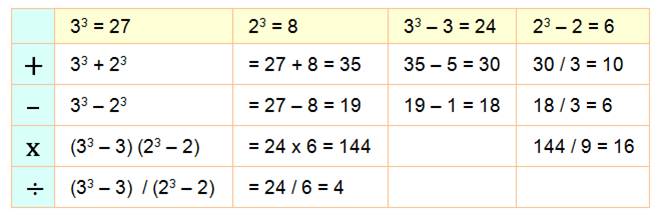|
||||||||||||||||||||||||||||||||||||||||
![]()
|
On
s’intéresse aux propriétés de divisibilité des
puissances des nombres. Sujet
productif car, en découlent :
|
|
A,
B et C sont des chiffres tels que: Trouvez
ces trois chiffres. |
|
|
||
|
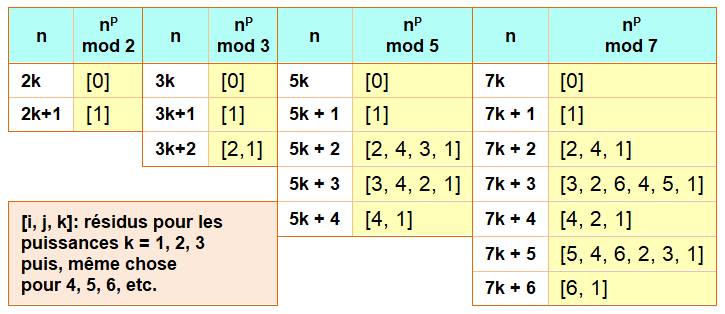
Un nombre
n à la puissance P divisé par n donne un reste nul. On écrit:
Voir
plus simple en mod et
ses applications Premières colonnes du tableau (mod
2) Un nombre
pair (n = 2k) à la puissance P est divisible par 2 (= 0 mod 2). Un nombre
impair (n = 2k + 1) à la puissance P, divisé par 2, donne un reste égal à 1. |
Colonnes suivantes du tableau (mod
3) Un nombre
divisible par 3 (n = 3k) à la puissance P est divisible par 3. Si le reste
du nombre est 1, le reste de la puissance quelconque est aussi 1 pour la division
par 3. Si le reste
du nombre est 2, le reste de la puissance est 2 pour les puissances impaires
et 1 pour les paires: alternativement: [2, 1]. |
|
|
|
||
Voir Petit
théorème de Fermat pour une autre vision de la divisibilité des puissances
![]()
|
NOMBRES en PUISSANCE –
Théorèmes |
|
|||
|
2n + 1 |
est
composé |
|||
|
2n – 1 |
est
premier |
si
n est premier (nécessaire, mais non suffisante) |
Fermat |
|
|
2n – 2 |
est
un multiple de 2n |
si
n est premier impair |
Fermat |
|
|
2n (2n+1 – 1) |
est
parfait |
si
(2n+1 – 1) est premier |
||
|
22^n + 1 |
n’est
pas toujours premier |
Fermat / Euler |
||
|
|
|
|
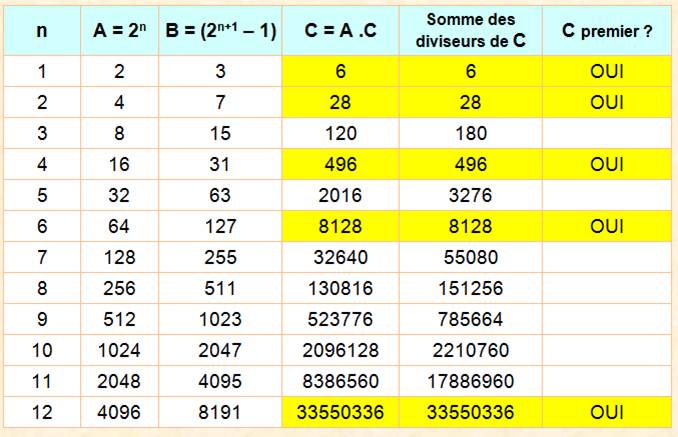
Euclide Calcul
et vérification pour n < 12
Conclusion Pour
trouver des nombres parfaits, il faut savoir reconnaître si 2n+1
– 1 est premier. |
|
|
|
||
|
Défi Fermat répond: "Il n'y en a aucun de 20 ni
de 21 caractères". Résolution Il
s'agissait de cherchez un nombre parfait entre 1020 et 1022. On passe
de n à n – 1 pour travailler avec la formule conventionnelle des nombres
parfaits. Alors,
un nombre parfait s'écrit aussi bien: 2n – 1 (2n
– 1) avec ce second
facteur, un nombre de Mersenne, premier. Calcul des exposants compatibles |
||
|
Limite
basse telle que: |
2n – 1 (2n – 1) = 1020 (20
chiffres) |
|
|
Négligeons
le -1 face au 2n. |
2n – 1 (2n ) =
1020 |
|
|
Passage
aux logarithmes: |
(n – 1) ln(2) + n ln (2) = 20 ln(10) |
|
|
Calcul: |
2n ln(2) – ln(2) = 20 ln(10) |
|
|
Valeur
de n min: |
|
|
|
Valeur
de n max: |
|
|
|
Recherche
des facteurs premiers: |
230 – 1
= 1 073 741 823 – composé 231 – 1 = 2 147 483 647 – premier 232 – 1
= 4 294 967 295 – composé 233 – 1
= 8 589 934 591– composé De toute
façon, l'exposant (32, 33 …) n'est pas premier, et le suivant est 37, mais il
faudra attendre 61 pour que le nombre complet soit premier … 261 – 1
= 2305843009213693951 – premier |
|
|
Recherche de nombres parfaits |
||
|
Aucun
nombre premier dans l'intervalle requis
de n = 33 à n = 36, donc pas de nombre parfait dans cet intervalle. 237
– 1= 137 438 953 471 =
223 x 616 318 177 |
Le
cas n = 31 avec 19 chiffres était connu de Frénicle, d'où le défi pour
trouver le suivant. Frénicle
savait sans doute que le nombre suivant à considérer était 237 – 1
et que la difficulté consistait à prouver que ce nombre de Mersenne est premier. Fermat
trouve la factorisation. Dans une lettre à Mersenne, il dit:" lequel
j'ai pourtant trouvé (…) être divisible par 223." Raté, pas de nombre
parfait à la clé. Il faut chercher plus loin. |
|
|
Nombres
parfaits avant
et après. |
230 (231 – 1) = 2,3 1018
(19
chiffres) = 2 305 843 008 139 952 128 260 (261 – 1) = 2, 6…1036 (37
chiffres) = 2 658 455 991 569 831 744 654 692 615 953
842 176 Ce nombre
ne sera connu qu'en 1883 >>> |
|
Voir Table
des facteurs des nombres de Mersenne
|
|
||
|
Propriété Soit deux nombres x et y à la puissance p,
avec p premier. Alors selon le petit
théorème de Fermat: xp – x
= k . p yp – y = h . p |
Différence (xp – yp)
– (x – y) = Kd . p La différence des puissances p,
diminuée de la différence des nombres, est un multiple de p. Idem pour addition, et multiple de p² pour la multiplication. Selon l'opération
|
|
|
Exemple
Attention, la division n'est pas toujours exacte! |
||
|
La barre de surlignement indique
qu'il s'agit des chiffres d'un nombre. Sans cela, ce serait le produit. Alors, il existerait
plusieurs solutions: 1x11+1
; 4 x 1 = 22+2; 4 x 2 = 22+2; 8 x 4 = 24+1 ;
9 x 1 = 31+1.
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Puissanc.htm |
![]()