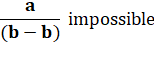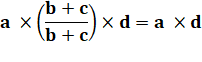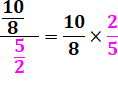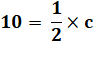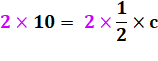f NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/12/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	BASES des CALCULS
Débutants Cours de 5^e	D'un bon pas!			Glossaire Nombres
INDEX Initiation au CALCUL Résolution de Problèmes	C'est clair	Parenthèses	Équations
		Sommaire de cette page >>> Opérations impossibles >>> Formation des nombres et retenues >>> Multiplications par 1 >>> Produits de négatifs >>> Fractions divisées >>> Parenthèses >>> Équations >>> Puissances >>> Formules en physique

Je ne suis pas sûr de moi en maths!

En finir avec les tracas de calcul,

Donner du sens à des formules vides …

Certaines personnes sont bloquées par les calculs. D'autres s'en sortent en apprenant par cœur des recettes de calculs. Ces recettes sont des raccourcis de calculs qui deviendront des automatismes. Pourtant, pour se rassurer, il est indispensable d'en connaître le fondement. Et, même pour ceux qui débutent, il est recommandé de prendre la peine d'écrire tout le procédé.

Voici quelques exemples de ces tracas pour débutants dont j'ai pu être le témoin. Une fois les principes revus, non seulement la personne est rassurée, mais prend goût aux maths. Elle réalise que les maths ne sont pas des trucs de magie pour initiés, mais bel et bien un édifice logique.

Opérations impossibles ou pas pour le moment, pas au programme
Il est interdit de soustraire un grand nombre d'un plus petit.	3 – 4 n'existe pas! (à l'école primaire)
Même en primaire, les enfants sont capables de comprendre que la soustraction donnera un nombre négatif. Négatif comme peut le devenir la température ou ma tirelire si je dois de l'argent.
Il est préférable d'annoncer que le résultat de cette opération est -1 et que les nombres négatifs seront vus dès la 6^e. On évitera l'incompréhension des parents: "Quoi? Le maitre t'a dit que cette opération est impossible! Je ne comprends pas!"

Il est interdit de diviser par 0.
Supposons que nous nous approchions de 0 avec un nombre aussi petit que vous voulez. Prenons 0,000 000 1, nombre que je peux introduire dans ma calculette. La division de 7 par ce nombre donne: 70 000 000. Autant de 0 dans les deux chiffres. Encore plus petit. Ajoutez mille 0 dans le premier, vous aurez mille 0 de plus dans la division (le quotient). Plus le nombre est proche de 0, plus le quotient grimpe vers l'infini.
La division par zéro conduit à introduire la notion d'infini et le concept de limite. Cela sera étudié plus tard. Pour le moment, ne divisons pas par 0, car les résultats seraient très farfelus.

Il est interdit de prendre la racine carrée d'un nombre négatif.	ce n'est en tout cas pas – 3.
La racine carrée de 9 est 3 car 3 x 3 = 9. Attention, c'est aussi – 3, car (-3) x (-3) = 9. Mais existe-t-il un nombre a tel que a x a = -9 ? Non, car c'est le nombre 3 qui va donner 9, mais le signe "–" est inatteignable. Nous avons bien (-3) x (+3) = -9, mais ce ne sont pas les mêmes nombres. L'un est positif et l'autre négatif. Oui, c'est impossible de prendre la racine carré d'un nombre négatif
La racine carrée d'un nombre négatif n'existe pas. Pour contourner la difficulté, les mathématiciens ont inventé les nombres imaginaires. Ils notent par convention: et alors: Note pour les puristes: on préfère noter i² = -1

Formation des nombres ou comment se propagent les retenues
Quand l'addition de deux chiffres dépasse 10, il a une retenue. J'ajoute le chiffre qui dépasse au calcul suivant.
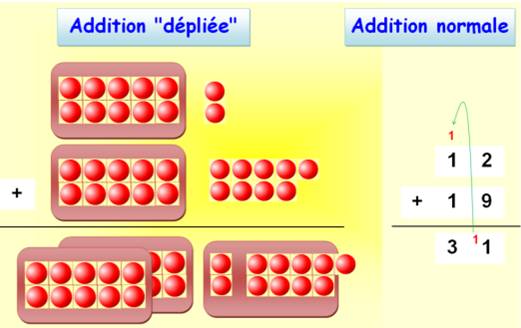
Exemple: Addition de 12 et 19. Écrire 12 est un raccourci pour dire: 1 fois 10 + 2 ou encore une enveloppe de 10 billes plus 2 billes. Ajouter 19, c'est ajouter une enveloppe de 10 billes et 9 billes. Je compte les enveloppes: 1 + 1 = 2 enveloppes. Je compte les billes toutes seules: 2 + 9 = 11. Je peux créer une nouvelle enveloppe de 10 billes et il en reste une toute seule. Au bilan: 3 enveloppes et 1 bille: 12 + 19 = 31.
La retenue est un mot qui veut simplement dire qu'il y a création d'une ou plusieurs enveloppes de 10 et que je n'oublierai pas (je retiendrai) d'ajouter à la somme des enveloppes existantes. La quantité d'enveloppes nouvelles (la retenue) est placée en haut de l'opération pour ne pas l'oublier. Avec l'habitude, on la mémorise sans la noter (calcul de tête). C'est notre système de comptage à base 10 qui permet ce report des retenues si pratique. Avec les chiffres romains, c'était beaucoup plus compliqué.
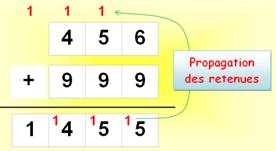
Exemple Colonne des unités: 6 + 9 = 15 soit 5 unités et une dizaine; je reporte la dizaine sur la somme de la colonne des dizaines. Colonne des dizaines: 1 de retenue + 5 + 9 = 15 soit 5 dizaines et une centaine; je reporte la centaine sur la somme des centaines.	Je vérifie l'addition aisément: 456 + 999 = 456 + 1000 – 1 = 1456 – 1 = 1455
Colonne des centaines: 1 de retenue + 4 + 9 = 14 soit une centaine et un millier. je reporte le millier sur la colonne des milliers. Colonne des milliers: 1 de retenue et rien d'autre. Je porte le résultat en bas.

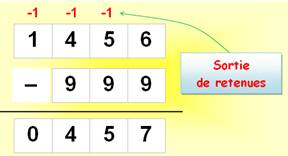
Avec la soustraction, la retenue marche à l'envers: il faut "déballer des enveloppes" pour soustraire un chiffre plus grand à un chiffre plus petit. Colonne des unités: 6 – 9 impossible; je prends une dizaine dans la colonne des dizaines et je retiens ce fait en notant -1 en haut de cette colonne. Alors 16 – 9 = 7.	Je vérifie la soustraction facilement: 1456 – 999 = 1456 – 1000 + 1 = 456 + 1 = 457
Colonne des dizaines: Je m'occupe de la retenue: 5 – 1 = 4 et je procède à la soustraction: 4 – 9 impossible. Avec une centaine empruntée à la colonne des centaines: 14 –9 = 5. Colonne des centaines: 4 – 1 = 3 puis 13 – 9 = 4 Colonne des milliers: Le 1 des milliers a été utilisé (retenue) pour le calcul des centaines. résultat: 0.

Éliminer les 1 ou le principe "une fois"
Dans une multiplication, j'ai le droit d'éliminer les 1.
Le nombre 1 est un nombre spécial pour la multiplication. Il est sans effet. On dit que c'est l'élément neutre de la multiplication. Notons que c'est le 0 qui est l'élément neutre de l'addition (0 + 1000 = 1000).
Le nombre 1 peut être caché. Ici, une fraction valant 1.
Avec des puissances. Un nombre à la puissance 0 vaut 1.

Produit de négatifs ou le principe "les ennemies de mes ennemis …"
Moins par moins donne plus.	(-2) x (-5) = 10
Comprendre cette opération nécessite une petite gymnastique intellectuelle. On comprend bien l'histoire de: les ennemis de mes ennemis peuvent être mes amis. Autre vision: si je fais un demi tour je me dirige dans le sens opposé (-); si je fais deux demi-tours (-) x (-), je reviens sur mes pas.
La multiplication avec nombres algébriques peut se comprendre avec la métaphore des gains à un pari. Je gagne deux fois la mise de 5 € ; j'empoche deux fois 5 €; 2 x 5 = 10 € Il gagne deux fois la mise de 5 € ; deux fois je donne 5 € ; 2 x (-5) = - 10 € Je perds deux fois la mise de 5 € ; je donne deux fois 5 € ; (-2) x 5 = -10 € Il perd deux fois la mise de 5 € deux fois j'empoche 5 € ; (-2) x (-5) = 10 €

Compter l'argent

Dès le plus jeune âge (6 ans et plus), les enfants d'aujourd'hui sont conscients de l'argent et même très demandeurs d'en savoir plus. Raisons: disponibilité d'un argent de poche et propension à vouloir s'acheter des objets-plaisirs. Les encourager à compter via des exemples pécuniaires est une bonne idée. Les nombres, les quantités et les calculs prennent une forme concrète. Une autre raison me pousse à insister sur ce point: le monde moderne est très porté sur la chose économique: vie familiale comme vie professionnelle. Distiller imperceptiblement les concepts de débit et crédit pourrait bien élever le niveau de la culture économique des jeunes Français.

Fractions divisées ou le principe renversant
Pour diviser une fraction par une autre, je multiplie par la deuxième renversée.
Je me persuade en prenant un exemple: 10 comprimés divisé par ½ (ou coupé en moitiés) me donneront 20 demi-comprimés. Autrement-dit 10 divisé par ½ = 20. On peut aussi poser: 10 / 0,5 = 20.
La division, au fait, c'est quoi? La division de a par b c'est chercher un nombre c tel que => Diviser a = 10 par b = ½, c'est chercher un nombre c tel que => La valeur de c se calcule en multipliant par 2 de chaque côté =>		a = b . c. c = 2 x 10 = 20.

Voir Division des fractions - Développements

Parenthèses ou le principe des paquets
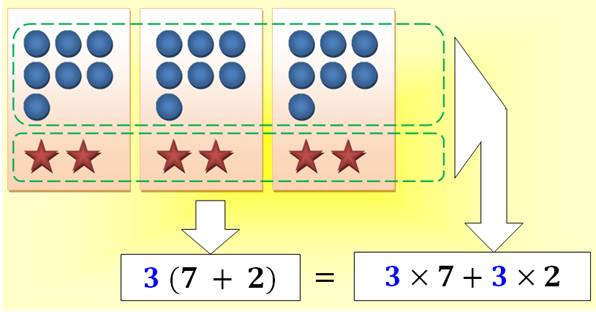
Si un nombre est devant une parenthèse renfermant une addition, je multiple chacun des termes par ce nombre	3 (7 + 2) = 3 x 7 + 3 x 2 a (b + c ) = a.b + a.c
Nous pouvons visualiser ce procédé très simplement: Chaque parenthèse représente un paquet qui contient sept boules et deux étoiles. Il y trois tels paquets. Nous pouvons compter ces objets de deux manières: avec les paquets (parenthèses): 3 paquets de 7boules et 2 étoiles; ou sans les paquets (pas de parenthèses): 3 fois 7 boules et 3 fois 2 étoiles.
Les parenthèses sont une convention d'écriture montrant des groupes de nombres (7 et 2) formant des paquets ayant des propriétés communes (ici: 3 fois le paquet, donc trois fois chacune des choses qu'il y a dans le paquet)
Le nombre de fois peut être lui aussi un paquet. Le même procédé s'applique en cascade. Et encore une fois pour chaque terme.	(1 + 2) (7 + 2) = (1 + 2) x 7 + (1 + 2) x 2 = (1 + 2) x 7 + (1 + 2) x 2 = 1 x 7 + 2 x 7 + 1 x 2 + 2 x 2

Équations ou le principe de la balance
Un nombre d'un côté passe de l'autre côté de l'égalité en changeant de signe.	5x + 10 5x	= 20 = 20 – 10 = 10
Imaginez une pesée. Le signe égal signifie que les deux plateaux de la balance sont en équilibre; au total, il y a le même poids de chaque côté. Chaque opération effectuée d'un côté, doit être effectuée de l'autre pour maintenir l'équilibre.
Dans notre cas, nous retirons 10 de chaque côté. Pour la même raison, si nous divisons par 5 d'un côté, l'équilibre est maintenu si nous divisons aussi par 5 de l'autre côté.	5x + 10 5x + 10 – 10 5x x	= 20 = 20 – 10 = 10 = 2
Une équation est comme une balance, toute opération exécutée d'un côté est à répéter de l'autre côté pour maintenir l'équilibre (l'égalité).

Puissance ou métamorphose de la multiplication en addition
La multiplication des puissances est réalisée en ajoutant les exposants.		10^2 x 10^3 a^2 . a^3	= 10^2 + 3 = 10^5 = a^2 + 3 = a^5
Que veut dire 10^2 ? C'est 10 x 10 = 100. Ce qui veut dire que 10 est multiplié 2 fois par lui-même. Même chose pour 10^3 = 10 x 10 x 10 = 1000. Mettre 2 ou 3 en exposant est une convention d'écriture, un simple raccourci d'écriture. Nous en connaissons un autre bien pratique avec la multiplication: en effet, 5 x 6 est un raccourci pour 6 + 6 + 6 + 6 + 6. Première remarque: dans les deux cas, la quantité de 0 est égale au nombre en exposant. Par exemple: 10^12, c'est un 1 suivi de douze 0. Parfois noté 10^12 ou même 10e12. Seconde remarque: Que vaut le produit 10^2 x 10^3. Développons: 10^2 x 10^3 = 100 x 1000 = 100 000 = 10^5 En quantité de zéros, nous avons: 2 + 3 = 5
La convention d'écriture des puissances conduit à transformer la multiplication des puissances en somme des exposants.
Exemples	10^2 x 10^3 x 10^-5 a^2 . a^3 . a^54 a^2 . b^3 . a^54 a^n . a^m . a^p a^n + a^n + a^p	= 10^2 + 3 – 5 = 10^0 = 1 = a^2 + 3 + 54 = a^59 = a^2 + 54 . b^3 = a^56 . b^3 = a^n + m + p = 2a^n + a^p (et non a^2n+p)

Voir Exemples de calculs

Formule en physique C'est la même chose qu'en mathématique
La formule de la vitesse en physique, je peux la changer?	L	= v . t
Aucune différence en physique et en mathématique, une égalité est une égalité. Longueur égale vitesse multipliée par le temps (la durée). Exemples: La voiture fonce à 130 km / h pendant 2 heures, elle parcourt L = v . t = 130 x 2 = 260 km. La balle de fusil met 1,2 secondes pour atteindre sa cible. Sa vitesse est de 1500 m /s. La cible est située à une distance de L = v . t = 1500 x 1,2 = 1800 m soit 1,8 km.
Toutes les opérations algébriques habituelles s'appliquent. Il suffit de garder l'égalité en appliquant à un côté ce que l'on applique à l'autre.
En divisant par t En divisant par v	v t	= L / t = l / v
Exemple: L'escargot trace son chemin avec une vitesse de 50 cm en 4 minutes. Sa vitesse est v = L / t = 50 / 4 = 12,5 cm / min. Soit 60 fois plus en 1 heure: 60 x 12, 5 = 750 cm ou 7,5 m.

Pourquoi cette page ?

Bien entendu, les informations ci-dessus sont développées avec plus de détails sur ce site. Mais, avec l'expérience des aides que j'ai pu prodiguer (via Internet et autres aides intuitu personae), j'ai cru bon de rassembler toutes ces tracas de calculs en une seule page. Idée renforcée à la lecture du livre d'Anne Siety, cité en référence. Sa grande expérience l'amène à décrire les raisons majeures conduisant au rejet des maths. L'une d'elles serait l'apprentissage de recettes de calcul sans bien comprendre pourquoi elles marchent. Elle insiste en disant que ces gens là, pour se rassurer, se mettent à faire ses tonnes d'exercices. Quel dommage! Alors que tout peut devenir plus simple et surtout plus logique.

Suite	Calculs – Explications pas à pas – Index Inéquations Innumérisme Éducation – Index
Junior	Les quatre opérations – Junior Arithmétique pour junior – Diaporamas Énigmes déroutantes vues sur le Net
Voir	Additions fallacieuses Additionneur Calcul mental – Index Carrés Magiques Débutants – Index Jeux – Index Preuve par neuf Somme des chiffres Tables de multiplication
Livre	Qui a peur des mathématiques – Anne Siety – Denoël – 2012 – L'auteur est une psychopédagogue qui travaille avec les personnes en difficulté avec les mathématiques.
Cette page	http://villemin.gerard.free.fr/Calcul/Operatio/CClair.htm