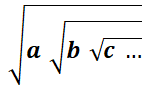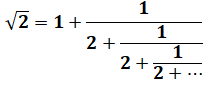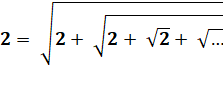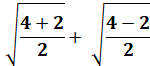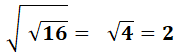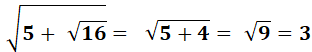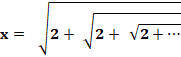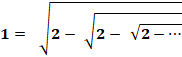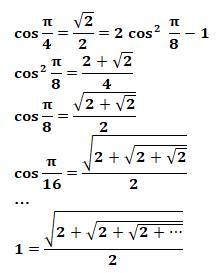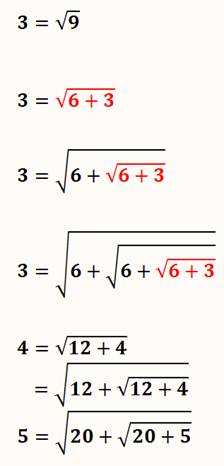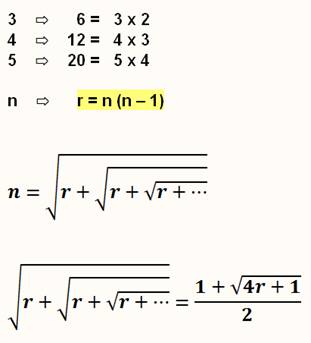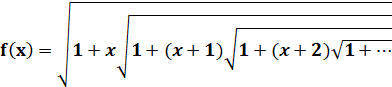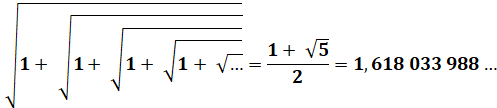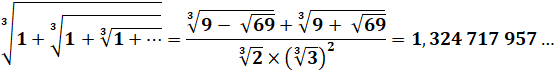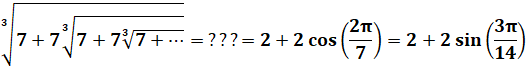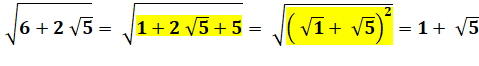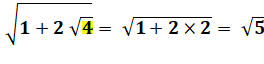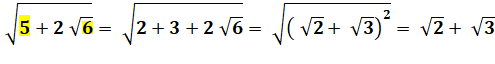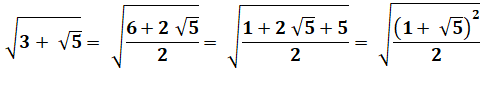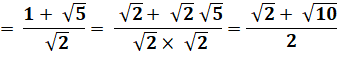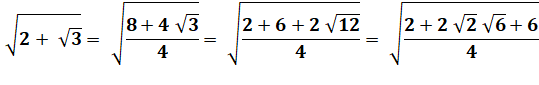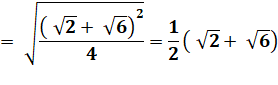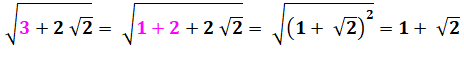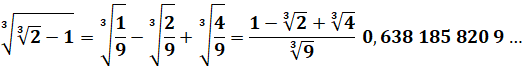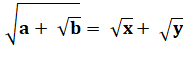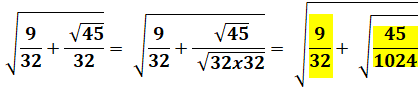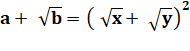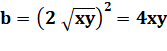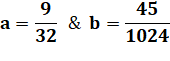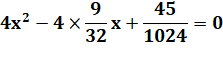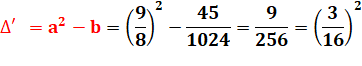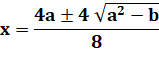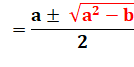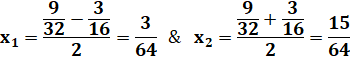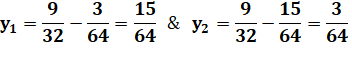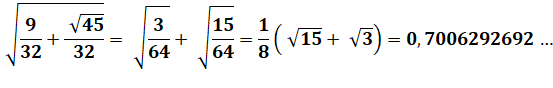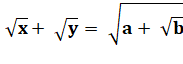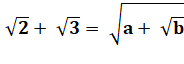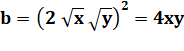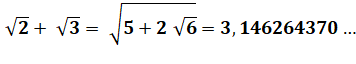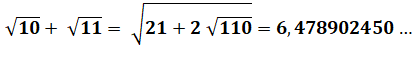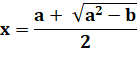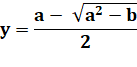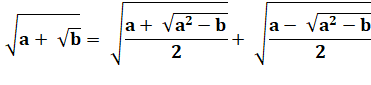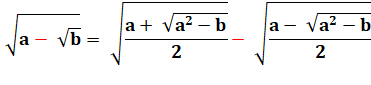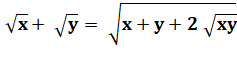|
||||||||||||||||||||||||||||
![]()
|
RACINES CONTINUES Racines (ou radicaux) emboîtées ou imbriqués Tous les
nombres peuvent s'exprimer avec une racine continue du type:
|
|
|
Il
existe les fractions continues, suite
sans fin d'étages de fractions qui finit par donner la valeur d'un nombre. De
même, il existe les racines continues,
suite de radicaux emboîtés
qui finissent par donner la valeur de tous les nombres entiers. |
|
Anglais: Nested surds,
nested radicals (nest veut dire: nid) /
Continued nested radical fraction (CNRF)
|
Simplifier une expression avec radicaux imbriqués
est généralement un problème difficile. Certains cas (rares) sont néanmoins calculables,
comme:
|
|
Curiosité |
Observez ces racines de deux! Et si sous le radical nous remplacions un 2 par sa
valeur en racine: Encore Vous avez compris que cela peut durer autant que
l'on veut. Et nous obtenons cette racine continue exprimant la
valeur de 2. |
|
|
|
Développons le calcul pour se rendre compte des
valeurs en jeu. En bleu le r |
|||
|
Démonstration |
Élévation au carré Remplacement par x Équation du second
degré Seule la racine
positive est retenue. |
x² = 2 + x x² – x – 2 = 0
=> x1 = 2 et x2
= -1 |
|
|
Cas avec -2 |
Avec le signe moins,
on trouve la racine continue de 1. |
x² + x – 2 = 0
=> x1 = 1 et x2
= -2
|
|
|
Démo Trigo |
On part de la valeur
du cosinus de Pi/4 et application de la formule de l'angle
double. Ce procédé est répété.
Calcul de la limite
lorsque le dénominateur est infini et l'angle nul; alors, cos 0 = 1 |
|
|
|
|||
|
Approche |
Si nous voulons recommencer l'exploit du 2, mais
cette fois avec 3, il faut un radical couvrant le carré de 3, soit 9. Faisons maintenant apparaître la valeur 3. Dans ces conditions, nous sommes en mesure de
reporter la valeur de 3 sous le radical. Et, évidemment, vous l'avez compris, de poursuivre
indéfiniment. Vous pouvez répéter cette procédure pour tous les
nombres. |
|
|
|
|
|||
|
Formules générales |
Observez la valeur sous les radicaux. Soit la formule générale. Et réciproquement, connaissant r. |
|
|
Voir Racines continues et formules
|
Tout nombre entier N est exprimable sous forme d'une
racine continue dont la valeur sous le radical est égale à n = N² - N |
Voir Ramanujan
|
Nombre 3 Principe
du calcul La
technique consiste à trouver une fonction qui peut être réintroduire sous le
radical. Une racine continue qui se contient elle-même. Connaissant
le profil (le degré) de la fonction, on calcule les coefficients numériques. Ici,
on trouve: f(x)
= x + 1 Avec
x = 2, la racine continue converge vers 3; avec x = 3, ces sera 4; etc. |
Cette racine continue tend
vers 3. Idée du
calcul** Soit la fonction: Remarquez que la fonction
se retrouve au deuxième rang, multipliée par x: Au carré: Degré 2 à gauche et x+1 à
droite: la fonction est linéaire: f(x) = ax
+ b f(x) = ax + b En remplaçant: La constante b² = 1 et b =
1 Équation satisfaite pour a
= 1 f(x) = x
+ 1 Or dans le cas numérique
qui nous intéresse: x = 2 et
f(x=2) = 2 + 1 = 3 |
Voir Calcul itératif
|
Nombre
d'or Golden ratio |
Solution
(une des) de l'équation: x2
– x – 1 |
|
Nombre
plastique Plastic constant |
Solution
(une des) de l'équation: x3
– x – 1 |
|
Nombre
d'argent Silver constant |
Solution
(une des) de l'équation: x3 – 5x2 + 6x – 1 Voir Nombre
d'argent / Trigonométrie
de Pi/7 / Autres
nombres d'argent Note:
la racine en 7 converge (selon mes calculs) vers 3,048917339. L'équation
comme les valeurs en sinus et cosinus sont bien égales à 3,246… Où est
l'erreur? La
racine numérique R peut s'écrire R3 = 7 + 7R, équation dont la
racine réelle est bien: 3, 04891… Conclusion:
cette égalité donnée en référence me
semble fausse, mais je n'ai pas réussi à la rectifier. |
|
|
||
|
L'astuce consiste à former
un carré en utilisant une identité remarquable. |
|
|
|
Parfois banal Carré sous le
radical |
|
|
|
Parfois facile On note que 6 = 3 x 2 et 3 + 2 = 5 |
|
|
|
Parfois relativement facile. Nécessite une
multiplication |
|
|
|
Parfois plus difficile Nécessite de
travailler sous le radical |
Voir Méthode générale |
|
|
Et souvent: impossible |
|
|
|
Mais, un simple changement
du 2 et 3 et c'est possible! |
|
|
|
Quelques
exploits de Ramanujan |
|
|
Problème de la réduction des radicaux |
Le problème
général de réduction des radicaux est un problème difficile: aussi bien pour
un calcul de tête que pour sa programmation
(computer algebra systems). En 1989, Susan
Landau (Américaine née en 1954) met au point les premiers algorithmes qui
permettent de savoir si la réduction des radicaux est possible. |
Voir Calcul du cosinus
de pi/n
|
|
||
|
Littéral |
Numérique |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Équation du second degré |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Résultat de la réduction |
|
|
|
|
|
|
|
|
|
|
|
|
a = 2+ 3 = 5 b = 4.2.3 = 24 = 2² .6 |
|
|
Résultat |
|
|
|
Autre exemple avec réponse immédiate |
|
|
Bilan
|
Réduction |
Radicalisation |
|
|
|
|
|
|
|
|
Résultat immédiat |
|
|
|
Mieux! Au cube …
|
Calcul
Résolution
algébrique On cherche
comment transformer ce qui est sous le radical en un cube. Voir comment. On trouve:
On se
retrouve simplement avec:
Autre
relations du même type
|
Autre
relations du même type
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()