|
|||||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATION DU PREMIER DEGRÉ Découverte
de la mise en équation avec quelques problèmes simples, expliqués
pas à pas.
|
Oups! C'est encore compliqué pour moi!
Et si on repartait d'un bon
pied ?
|
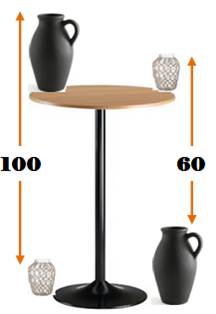
Quelle est la hauteur
de cette table ? On trouve aussi cette énigme
avec un chat sur la table et une tortue au sol. |
|
|
|||
|
C'est nul! |
5x x |
= 0 = 0 |
|
|
Classique et simple Pensez aux
plateaux d'une balance, ils doivent toujours être équilibrés. C'est
pourquoi on agit de la même manière de chaque côté |
x – 2 x – 2 + 2 x |
= 0 = 0 + 2 = 2 |
|
|
Nécessité de développer la parenthèse |
5 (x – 2) 5x – 10 5x x |
= 0 = 0 = 10 = 10 / 5 = 2 |
|
|
Pa plus compliqué si l'égalité n'est pas nulle |
5 (x – 2) 5x – 10 5x x |
= 90 = 90 = 90 + 10 = 100 = 100 / 5 = 20 |
|
|
Échanges de bons procédés entre parenthèses |
5 (x – 2) 5x – 10 5x – 6x – x x |
= 6 (x – 5) = 6x – 30 = 10 – 30 = –20 = 20 |
|
|
Fractions |
|
|
|
|
Produits en croix |
|
|
|
|
|
10 (x + 2) 10x + 20 40 x – 10 x 30x x |
= 2 (20x + 9) = 40x + 18 = 20 – 18 = 2 = 1 / 15 |
|
|
Compliqué? |
|
|
|
Voir Racines carrées |
x² x |
= 4 = 2 (ou –2) |
|
Presque second degré Un produit est nul si un de ses
facteurs est nul. |
(x – 1) (x – 2) x – 1 x – 2 |
= 0 = 0 et x = 1 = 0 et x = 2 |
|
Même chose, mais cachée! Deux nombres dont la somme est -3 et
le produit -10: 2 et – 5 conviennent. Rappel: (x + a) (x +
b) = x² + x(a + b) a.b |
x² – 3x – 10 (x + 2) (x – 5) x + 2 x – 5 |
= 0 = 0 = 0 et x = – 2 = 0 et x = 5 |
|
Dément … Rappel: a² – b² = (a + b) (a – b) |
x² – 2x + 1 (x – 1)² (x – 1)² –
(3x – 7)² (x – 1 + 3x –
7) (4x – 8) (–2x + 6) 4x – 8 2x – 6 |
= 9x² – 42x + 49 = (3x – 7)² = 0 (x
– 1 – 3x + 7) = 0 = 0 = 0
et x = 2 = 0
et x = 3 |
Voir Factorisation
/ Identités remarquables / Équation du second degré
|
Mise en équation Facture de 120 euros. Elle comprend un
abonnement de 60 euros et une consommation qui coûte 20 euros par heure. Combien d'heures de consommation? |
Quantité d'heures Consommation Facture Résolution Résultat |
= x = 20 x = 20 x + 60 = 120 20x = 120 – 60 = 60 x
= 60/20 = 3 |
|
Un rectangle
dont l'aire: 50 cm². Il est deux fois plus long que large.
Quelles sont ses dimensions? |
Longueur Largeur Aire L² L l |
= L = l = ½ L = L.l = ½ L² = 50 = 50 x 2 = 100 = 10 = 10 / 2 = 5 |
|
3 bières et 2 cocas = 6,10 euros 5 bières et 1 coca = 7,60 euros Prix de chaque bouteille? Voir Système
d'équations Voir Poids du tonneau |
3b + 2c 5b + 1c 3b + 2c 10b + 2c 7b b 5 x 1,30 + 1c c |
= 6,10 = 7,60 = 6,10 = 15,20 = 9,10 = 1,30 = 7,60 = 7,60 – 6,50 = 1,10 |
|
70 pattes pour 25 bêtes. Combien de chaque? |
Lapins Canards Bêtes Pattes C 4L + 2(25 – L) 2L – 50 L C |
= L = C L + C = 25 4L+ 2C
= 70 = 25 – L = 70 = 70 = 10 = 15 |
|
Somme de 545 euros en 93 billets de 5 et de 10 euros.
Combien de chaque? |
Billets de 5 € Billets de 10 € Somme Billets Différence |
5C 10D 5C
+ 10D = 545 C
+ 2D = 109 C
+ D = 93 2C + 2D = 186 C
= 186 – 109 = 77 D
= 93 – 77 = 16 |
|
|
|||||||||||||||||
|
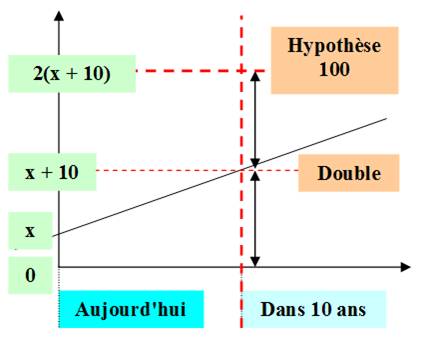
Problème Dans 10 ans, le double de l'âge de Pierre sera 100 ans. Solution Assez évidente: dans 10 ans, Pierre aura la moitié de
100 ans, soit 50 ans; il a aujourd'hui 10 ans de moins, soit 40 ans. Un simple raisonnement suffit; on peut le suivre de
tête. Néanmoins, nous allons mettre ce problème en équation en tant
qu'exemple utile pour traiter des cas plus compliqués. Équation Notons: x
l'âge de Pierre aujourd'hui et y son âge futur.
Résolution
Illustration
|
|||||||||||||||||
|
|
|||||||||||||||||||||||||
|
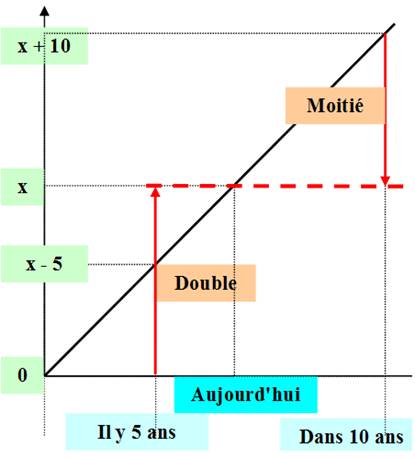
Problème Dans 10 ans, la moitié de l'âge de Pierre sera le
double de cet âge il y a 5 ans. Solution Un raisonnement ne suffit plus; il est difficile de
faire de tête. Il faut mettre ce problème en équation. Équation Inconnue: X
est l'âge d'aujourd'hui.
Résolution
Illustration
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
Problème Pour payer les ouvriers, si le patron:
Combien d'ouvriers ? Équation
|
|||||||||||||||||||||||||
Manuel d'algèbre de Clairaut (1713 - 1765)
|
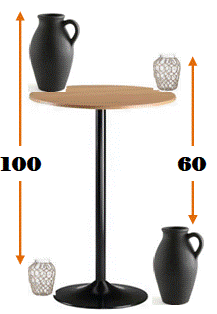
Mise en équations Hauteur
T de cette table ? On
a un grand vase G et un petit vase P. On
note les hauteurs mentionnées sur la figure: En
additionnant: Solution par raisonnement
Les
mesures de droite (60) sont associées à une deuxième table placée en dessous
de la première. Alors,
la mesure 100 + 60 s'applique à deux tables (le grand vase étant présent dans
un cas et absent dans l'autre). La
table mesure donc: 160 / 2 = 80 cm. |
![]()
|
Suite |
||
|
Voir |
||
|
Cette page |
|
|
![]()