|
|||||||||||||||||||||||||||||||||||||
![]()
|
Équation ax + by + c Identité de Bézout Une telle équation
possède-t-elle toujours des solutions ? Si oui, quelles sont leurs
propriétés ? |
|
|
||
|
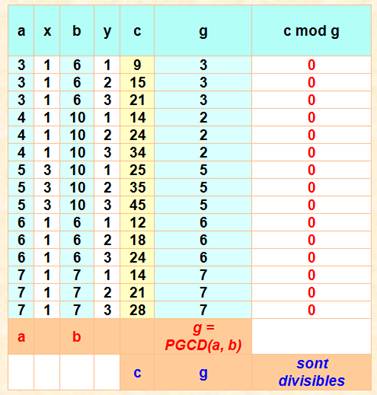
Calcul de c =
ax + by Observons la valeur de c pour quelques valeurs de x et y. Comparons à g,
le PGCD de a et b. Rappel
sur le modulo c mod g veut dire
pratiquement "reste de la division de c par g". On
remarque que: Chaque fois que l'égalité ax + by = c est satisfaite alors,
c est divisible par le PGCD de a et b. |
|
|
|
|
||
|
Par définition du
PGCD |
a = g . k b = g . h |
|
|
L'équation devient |
g . k . x + g . h . y
= c g ( k . x + h . y) = c |
|
|
Conclusion |
c est divisible par g |
|
|
|
||
|
Théorème Pour que l'équation ax + by = c admette une solution en nombres entiers il faut et il suffit que le PGCD de a et b divise
le nombre c. |
Il existe alors, au moins, une
solution x0 , y0 Les autres solutions, si elles
existent, sont données par la relation : x = x0 – k . b / g y = y0 +
k . a / g où k est un
entier (relatif) et g = PGCD(a,b) |
|
|
|
|||
|
Théorème Si PGCD (a, b) = c, alors il existe 2 entiers relatifs x et y (positifs ou négatifs) tels que: ax + by = c. |
Exemple 105 x + 33 y + c = 0 Trouvez c minimum et les solutions
de l'équation. Méthode
rapide de calcul du PGCD 33 = 11 x 3 et 105 est divisible par 3 et pas par
11; alors PGCD(33, 105= ) 3 Calcul
du PGCD (Algorithme
d'Euclide) pour trouver la solution de notre équation
|
||
|
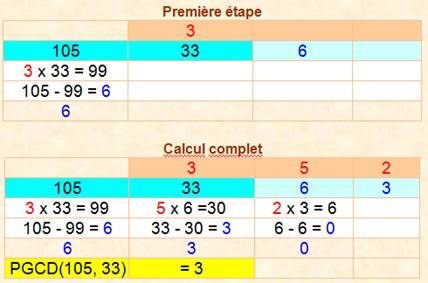
Écrivons ces relations pour mieux
les visualiser |
105 33 6 |
= 33 x 3 + 6 = 6 x 5 + 3 = 3 x 2 |
|
|
Puis remontons l'envers, en
s'intéressant au PGCD |
3 3 3 |
=
33 – 6 x 5 =
33 – (105 - 33 x 3) x 5 =
33 x 16 – 105 x 5 |
|
|
On dispose ainsi d'une solution: |
|
16 et 5 |
|
Humour de mathématicien
|
Ça
commence par un Bézout et ça finit par un Gauss et un Landau. Cité par Les-Mathématiques.net |
Voir Pensées & humour / Mathématiciens
|
Cas
ou le PGCD vaut 1 |
|
|
|
Dans ce cas, par hypothèse, a
et b sont premiers entre eux. Et, si PGCD (a, b) = 1 = c, alors, ax + by = 1 ou, à
l'envers |
Théorème S'il existe
deux nombres x et y tels que ax + by = 1 alors a et b sont premiers entre eux |
|
Voir Identité de Bézout / Exemple pratique
|
|
||
|
Claude Gaspard
Bachet de Méziriac 1581
– 1638 |
En 1621, il a donné les
résultats exposé ci-dessus. Il
publie le texte de Diophante en le corrigeant et le généralisant C'est
cette édition que possédera Fermat. Il
publie son livre: " Problèmes plaisants et délectables " et
donne la résolution des équations ax + by = c Il
montre que si a et b sont premiers entre eux ax
+ by = 1 a
toujours une solution (Identité de Bézout). |
|
|
Moderne |
On parlera, en langage mathématique
moderne, d'ensemble quotient. Ensemble quotient d'un ensemble E
par une relation d'équivalence R :
ensemble des classes d'équivalence modulo R, noté : E/R. |
|
|
|
|||
|
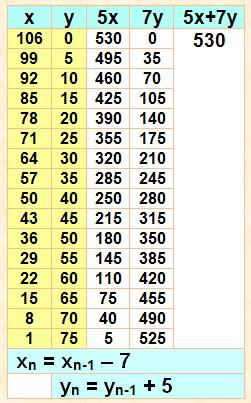
Résoudre 5x + 7y = 530 Solutions Il y a 16 solutions positives, et
une infinité de solutions négatives. |
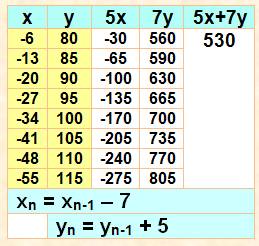
Solutions
positives et quelques solutions
négatives
|
||
|
Résolution |
5x + 7y = 530 |
||
|
On part d'une solution évidente |
Ici: y = 0 => x = 106 |
||
|
On utilise les formules impliquant
les coefficients opposés à l'inconnue |
xn = xn-1 – 7 yn = yn-1 + 5 |
||
|
Application |
|
||
|
80 personnes prennent un bus. Les unes payent 5 € et les autres 7
€. Le chauffeur encaisse 530 €. Combien de personnes payent le
premier prix et combien le second ? |
Posons les
équations |
x + y = 80 5x + 7y = 530 |
|
|
La deuxième
équation donne 16 solutions |
Voir ci-dessus |
||
|
Laquelle donne
x + y = 80? |
x = 15 y = 65 |
||
|
Résolution d'équations diophantiennes |
|
||
|
Rappel deux variables |
|||
|
Équation |
a.x + b.y |
= c |
|
|
Solution si |
g = (a, b) |
|
|
|
Racine primitive |
a.x + b.y |
Voir Calcul |
|
|
Alors, il y a une infinité de solution
selon la valeur de t |
X Y |
= x + t. b / g = y - t. a / g |
|
|
Avec trois variables |
|
||
|
Équation |
a.x + b.y + c.z |
= d |
|
|
Solution si |
g = (a, b, c) |
|
|
|
Racines primitives |
a.x + (b, c) u b.y + c.z |
= d = (b, c) |
|
|
Solution |
X Y Z |
= x + t. (b, c)
/ g = y.u – t (a.y / g) + s(c / (b, c)) = z.u – t (a.z / g) – s (b / (b, c)) |
|
En rouge, PGCD et
parenthèses signifiant PGCD
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()