NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/09/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
	Chapelet de cercles			Trois cercles – Tangents
				Trois cercles – Tr. Équilatéraux
				Quatre cercles – Construction
		Sommaire de cette page >>> Trois cercles – Problème classique >>> Approche >>> Deux sécantes >>> Triangles équilatéraux >>> Propriétés >>> Triangle équilatéral – Démonstration

Trois cercles

et triangles équilatéraux

Découverte d'une figure surprenante avec trois cercles et deux sécantes. Création de triangles équilatéraux.

Trois cercles – Problème classique		haut
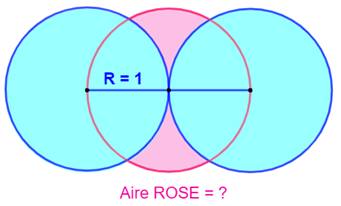
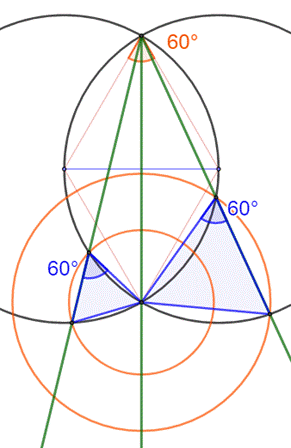
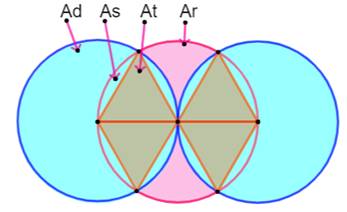
Pour commencer cette page … Construction Trois cercles de même rayon (R = 1) de centres alignés. Les centres des deux cercles tangents sont les extrémités d'un diamètre du cercle central. Quelle est l'aire de la zone rose ? Piste Les quatre triangles sont équilatéraux (côtés = rayon) L'aire de l'un des disques (Ad) est égale à: 4 fois le triangle équilatéral (At), 8 fois le segment (As), et 1 fois la zone rose (Ar)
Calculs

Approche
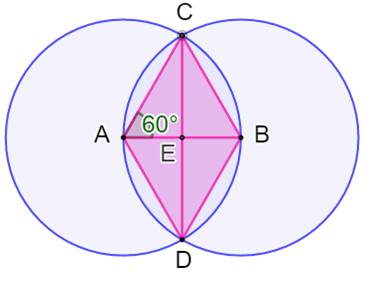
On connait la figure classique des deux cercles qui forment deux triangles équilatéraux tête-bêche. Construction 1. Segment AB. 2. Cercles (A, AB) et (B, AB). Intersections C et D. 3. Les triangles ABC et ABD sont équilatéraux. Le quadrilatère ACBD est un losange. Mesures Si AB = a, alors CD = .	Dans le triangle ABC, les côtés AB, BC et CA sont des rayons égaux; le triangle est équilatéral.

Deux sécantes
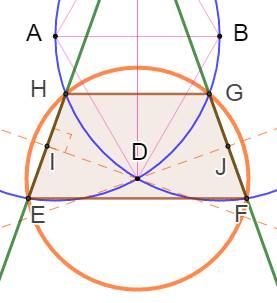
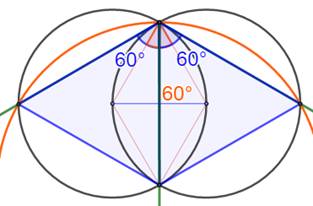
Les deux sécantes CE et CF, issues de C et symétriques par rapport à CD, découpent un trapèze isocèle EFGH sur les deux cercles. La symétrie induit: CH = CG, CE = CF ou encore HE = GF. Les segments HG et EF sont alors parallèles. Le quadrilatère EFGH avec deux côtés opposés parallèles et les deux autres égaux et symétriques est un trapèze. Un trapèze isocèle est inscriptible dans un cercle (Figure du bas) Son centre, point de concours des médiatrices ID et JD, est le point D, intersection des deux cercles.	Deux sécantes Cercle circonscrit du trapèze isocèle

Triangles équilatéraux
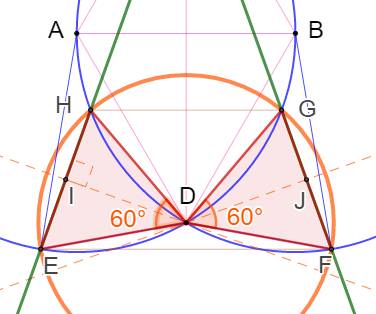
Dans le quadrilatère EFGH de centre D, les triangles DEH et DFG sont équilatéraux. Ils sont isocèles par construction (rayons du cercle orange). Reste à montrer que HE est aussi égal à un rayon ou que l'un des angle est égal à 60°. Le calcul analytique le montre. La démonstration purement géométrique est décrite in fine.

Propriétés avec trois cercles et deux sécantes
Deux cercles de même rayon dont l'un passe par le centre de l'autre. Un troisième cercle de rayon plus petit et centré une des intersections des deux cercles. Les quatre nouvelles intersections forment un trapèze isocèle et deux triangles équilatéraux internes et issus du centre du trapèze.
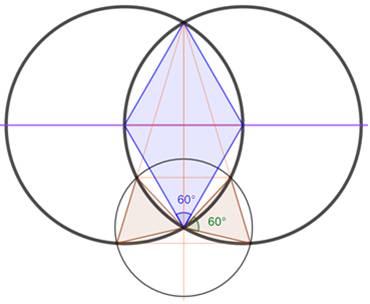
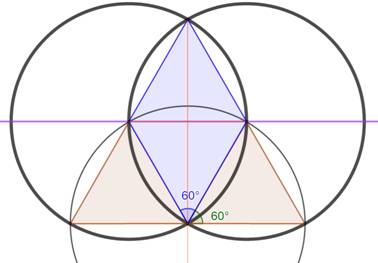
Cas général: Troisième cercle de rayon quelconque	Cas particulier: Les trois cercles ont le même rayon
Cas de sécantes quelconques >>> Il n'est pas nécessaire que les sécantes soient symétriques pour obtenir les triangles équilatéraux. Dans ce cas, le quadrilatère est quelconque et les quatre points ne sont plus cocycliques.
Cas particulier: le troisième cercle passe par l'autre intersection

Triangle équilatéral – Démonstration
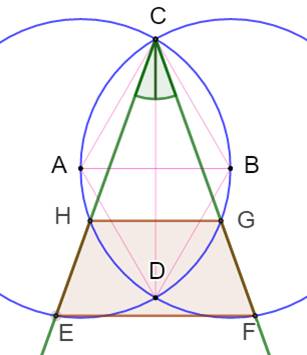
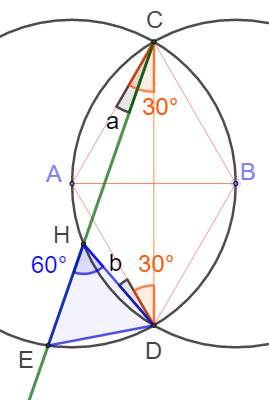
Problème Démontrer que l'angle bleu en H vaut 60°. Démontrer que l'angle en E vaut aussi 60° et que, par conséquent, le triangle DEH est équilatéral. Figure Deux cercles noirs de même rayon dont l'un passe par le centre de l'autre. Sécante verte qui forme le triangle bleu avec les intersections des cercles. Démonstration L'angle inscrit en E intercepte l'arc CD qui est intercepté par l'angle en A, lequel vaut 120°. L'angle en E vaut la moitié soit: 60°. Les angles inscrits a et b interceptent le même arc AH; ils sont égaux (même mesure). Dans le triangle CHD, la somme des angles: 180 = (30 – a) + (180 – x) + (30 + b) x = 60° = Angle en H.

Voir Application à la construction d'un angle de 60° passant par un point extérieur à une droite

Suite	Construction du triangle équilatéral circonscrit à un cercle Sangakus – Autres constructions géométriques Arbelos Carré et deux cercles tangents Cercle inscrit Chaine de Pappus Puissance d'un point par rapport à un cercle Quatre cercles Rayon du cercle circonscrit Sangakus
Voir	Bissectrices Cercle – Index Cercles et triangles Cône	Diamètre Géométrie – Vocabulaire Périmètre Rosace Sphère
Site
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/TroisCTE.htm